2 replies to this topic

[Ispectorgadget]

Cho tam giác $ABC$ có diện tích $S, M$ là trung điểm $BC$. Gọi $F$ là điểm thuộc $BM$. Đường thẳng qua $F$ và song song $AM$ cắt $AB$ tại $E$. Tìm vị trí của $F$ trên $BM$ để tam giác $ EFC$ có diện tích lớn nhất.

Edited by E. Galois, 28-06-2014 - 11:06.

[ChinhLu]

Cho tam giác $ABC$ có diện tích $S, M$ là trung điểm $BC$. Gọi $F$ là điểm thuộc $BM$. Đường thẳng qua $F$ và song song $AM$ cắt $AB$ tại $E$. Tìm vị trí của $F$ trên $BM$ để tam giác $ EFC$ có diện tích lớn nhất.

Let $x$ be the proportion $\frac{BE}{BA}$, which vaies from $0$ to $1$. The area of the triangle EFC can be easily computed in terms of $x$ and $S$ by

$$S(EFC) : = Sx\left(1-\frac{x}{2}\right).$$

Then the maximum is attained at $x=1$ which corresponds to $F=M$. 

 

 

 

 

To mod: I think English is universal and everybody can understand (otherwise one should reconsider himself, herself). On the other hand, typing vietnamese characters is terrible for me (because of my keyboard). 

Edited by ChinhLu, 28-06-2014 - 17:49.

[Kool LL]

Trong tứ giác lồi bất kì có 3 cạnh bằng $a$ cho trước, hãy tìm tứ giác có diện tích lớn nhất.

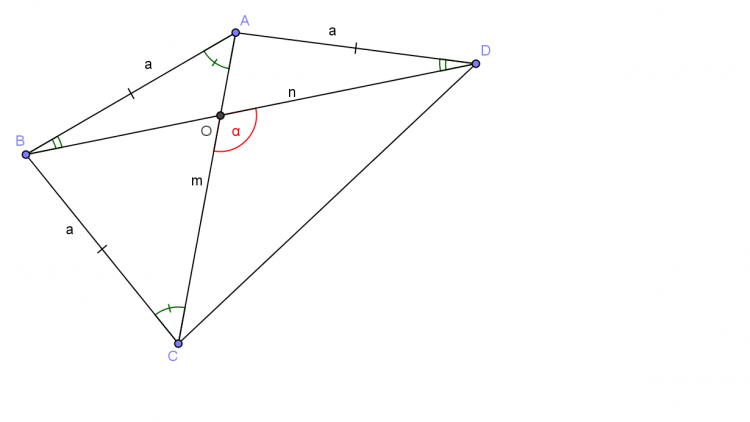
Ta có : $m=2a.\sin\left(\frac{\widehat{B}}{2}\right);\ n=2a.\sin\left(\frac{\widehat{A}}{2}\right);$

$\alpha=180^o-\widehat{BAC}-\widehat{ABD}=108^o-\frac{180^o-\widehat{B}}{2}-\frac{180^o-\widehat{A}}{2}=\frac{\widehat{A}+\widehat{B}}{2}$, với $\widehat{A}=\widehat{BAD};\ \widehat{B}=\widehat{ABC}$

$\Rightarrow S_{ABCD}=\frac{1}{2}\left|\overrightarrow{AC}\text{ x }\overrightarrow{BD}\right|=\frac{1}{2}m.n.\sin\alpha=2a^2.\sin\frac{A}{2}\sin\frac{B}{2}\sin\left(\frac{A+B}{2}\right)$

Do $0<A,B<180^o\Rightarrow 0<\frac{A}{2};\frac{B}{2}<90^o$ và hàm $\sin$ là hàm lõm dương trong khoảng $(0,90^0)$ nên suy ra :

$\sin\frac{A}{2}\sin\frac{B}{2}\overset{\text{Côsi}}{\le}\left(\frac{\sin\frac{A}{2}+\sin\frac{B}{2}}{2}\right)^2\overset{Jensen}{\le}\sin^2\left(\frac{A+B}{4}\right)$

$1=\frac{\sin^2\left(\frac{A+B}{4}\right)}{3}+\frac{\sin^2\left(\frac{A+B}{4}\right)}{3}+\frac{\sin^2\left(\frac{A+B}{4}\right)}{3}+\cos^2\left(\frac{A+B}{4}\right)$$\overset{\text{Côsi}}{\ge}4.\sqrt[4]{\frac{\sin^6\left(\frac{A+B}{4}\right)\cos^2\left(\frac{A+B}{4}\right)}{3^3}}=\frac{4\sqrt[4]{3}}{3}.\sqrt{\sin^3\left(\frac{A+B}{4}\right)\cos\left(\frac{A+B}{4}\right)}$

$\Rightarrow S\le 2a^2.\sin^2\left(\frac{A+B}{4}\right).2.\sin\left(\frac{A+B}{4}\right).\cos\left(\frac{A+B}{4}\right)\le 4a^2.\frac{3\sqrt{3}}{16}=\frac{3\sqrt{3}}{4}a^2$

Dấu $"="$ xảy ra $\Leftrightarrow\begin{cases}A=B \\ \sin^2\left(\frac{A+B}{4}\right)=3.\cos\left(\frac{A+B}{4}\right)\end{cases}\Leftrightarrow A=B=120^o$

Vậy hình thang cân (đáy nhỏ = cạnh bên = a, đáy lớn = 2a) sẽ có diện tích lớn nhất và bằng $\frac{3\sqrt{3}}{4}a^2$.