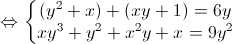$\left\{\begin{matrix} y^2 + x + xy -6y + 1 = 0 & \\ y^3x - 8y^2 + x^2y + x = 0 & \end{matrix}\right.$
2)
$\left\{\begin{matrix} y + xy^2 = 6x^2 & \\ 1 + x^2y^2 = 5x^2 & \end{matrix}\right.$
Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 01-02-2012 - 22:30