$\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca} \ge 1$
CMR:
$\frac{a}{bc}+\frac{b}{ca}+\frac{c}{ab} \ge 1$
Em So-zi, các anh thử làm đi
Bài viết đã được chỉnh sửa nội dung bởi ductai199x: 19-02-2012 - 22:45


Bài viết đã được chỉnh sửa nội dung bởi ductai199x: 19-02-2012 - 22:45

Off vĩnh viễn ! Không ngày trở lại.......

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 21-02-2012 - 12:12
BÙI THẾ VIỆT - Chuyên gia Thủ Thuật CASIO
• Facebook : facebook.com/viet.alexander.7
• Youtube : youtube.com/nthoangcute
• Gmail : [email protected]
• SÐT : 0965734893

Bài viết đã được chỉnh sửa nội dung bởi nguyenta98: 20-02-2012 - 21:37

=.= em làm dài quá anh ngại đọc. Cách khác ngắn hơn cho a,b,c dương và $a+b+c\geq abc$ chứng minh $a^2+b^2+c^2\geq abc$Giải như sau:
Đề tương đương cho $a+b+c\geq abc$ chứng minh $a^2+b^2+c^2\geq abc$
$\left\{\begin{array}{1}a+b+c\geq abc \\a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}{3} \end{array}\right. \rightarrow \left\{\begin{array}{1}(a+b+c)^2\geq abc(a+b+c) \\a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}{3} \end{array}\right. \rightarrow a^2+b^2+c^2\geq \dfrac{(a+b+c)^2}{3}\geq \dfrac{abc(a+b+c)}{3}$
TH1: $a+b+c\geq 3 \rightarrow \dfrac{abc(a+b+c)}{3}\geq abc \rightarrow a^2+b^2+c^2\geq abc \rightarrow Q.E.D$
TH2: $a+b+c<3$ <1>
Đến đây có 2 TH
Th1: Một số $\geq 1$ hai số $\le 1$ giả sử $a\geq 1$ và $b,c\le 1$ khi đó $\dfrac{a}{bc}\geq 1$ do đó có $đpcm$
Th2: Hai số $\geq 1$ một số $\le 1$ giả sử $a\geq 1, b\geq 1, c\le 1 \rightarrow a=1+x,b=1+y,c=1-z$
Kết hợp <1> có $a+b+c<3 \rightarrow x+y-z<0$ và $a,b,c>0$ nên $z<1$ <*>
Ta có $a^2+b^2+c^2=(1+x)^2+(1+y)^2+(1-z)^2=3+x^2+y^2+z^2+2x+2y-2z (2)$
$abc=(1+x)(1+y)(1-z)=(1+x+y+xy)(1-z)=xy+x+y+1-z-xz-yz-xyz (3)$
Ta sẽ chứng minh $(2)>(3) \rightarrow 3+x^2+y^2+z^2+2x+2y-2z>xy+x+y+1-z-xz-yz-xyz \rightarrow 2+(x^2+y^2-xy)+z^2+x+y+xz+yz+xyz>z$
Ta thấy $z<1$ (do <*>) do vậy $2>z$ và $x^2+y^2-xy>0$ nên $2+(x^2+y^2-xy)+z^2+x+y+xz+yz+xyz>z \rightarrow Q.E.D$
Tuy nhiên dấu $=$ khi nào nhỉ? chỉ cần tìm ra một dấu bằng là xong, có thể xét vài giá trị riêng
Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 21-02-2012 - 12:48
►|| The aim of life is self-development. To realize one's nature perfectly - that is what each of us is here for. ™ ♫

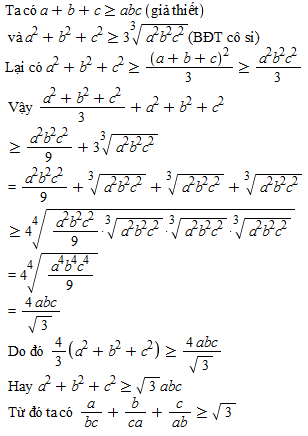
Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 21-02-2012 - 12:22
BÙI THẾ VIỆT - Chuyên gia Thủ Thuật CASIO
• Facebook : facebook.com/viet.alexander.7
• Youtube : youtube.com/nthoangcute
• Gmail : [email protected]
• SÐT : 0965734893

Bạn có thể chỉ lỗi sai cho mình được khôngThế này nhé, có thể đề bài ở đầu sai (vì $a, b, c$ khác 0) và cũng như thế, tôi nghĩ tới 1 BĐT đúng hơn (Thỏa mãn dấu dẳng thức sảy ra):
Cho các số dương $a, b, c$ thỏa mãn $\frac{1}{ab} + \frac{1}{bc} + \frac{1}{ca} \geq 1$
Chứng minh: $\frac{c}{ab} + \frac{a}{bc} + \frac{b}{ca} \geq \sqrt{3}$
Sau đây là chứng minh:
P/S: Đôi khi dùng phản chứng lại sai (Thế mới chán !!!)
►|| The aim of life is self-development. To realize one's nature perfectly - that is what each of us is here for. ™ ♫

Đây chính là lỗi sai cơ bản:=.= em làm dài quá anh ngại đọc. Cách khác ngắn hơn Đề tương đương cho $a+b+c\geq abc$ chứng minh $a^2+b^2+c^2\geq abc$
Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 21-02-2012 - 12:50
BÙI THẾ VIỆT - Chuyên gia Thủ Thuật CASIO
• Facebook : facebook.com/viet.alexander.7
• Youtube : youtube.com/nthoangcute
• Gmail : [email protected]
• SÐT : 0965734893
0 thành viên, 0 khách, 0 thành viên ẩn danh