Chủ đề này có 10 trả lời

[Ispectorgadget]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu I (2.0 điểm). Cho hàm số: $y = \dfrac{x+3}{x+1}$ có đồ thị là $(H)$
1) Khảo sát và vẽ đồ thị $(H).$
2) Cho đường tròn $©$ có phương trình $(x+1)^2+(y-1)^2=\dfrac{16}{5}.$ Tìm tất cả các điểm $M$ thuộc $©$ sao cho tiếp tuyến tại $M$ của $©$ cũng là tiếp tuyến của $(H)$
Câu II. (2.0 điểm)
1) Giải phương trình lượng giác : $\dfrac{\cos^2 x-4}{3+4\sin x -\cos 2x}=\cot^2 \left(\dfrac{x}{2} + \dfrac{\pi}{4} \right)\left(\dfrac{1}{2} - \sin x \right)$
2) Giải hệ phương trình : $\begin{cases} x + \sqrt{x^2-2x+5} =3y + \sqrt{y^2+4} \\ x^2-y^2-3x+3y+1=0 \end{cases}$

Câu III. (1.0 điểm). Tính $I=\displaystyle \int _{0}^{1} \dfrac{1+(2+x)xe^{2x}}{1+xe^x}\mbox{d}x$

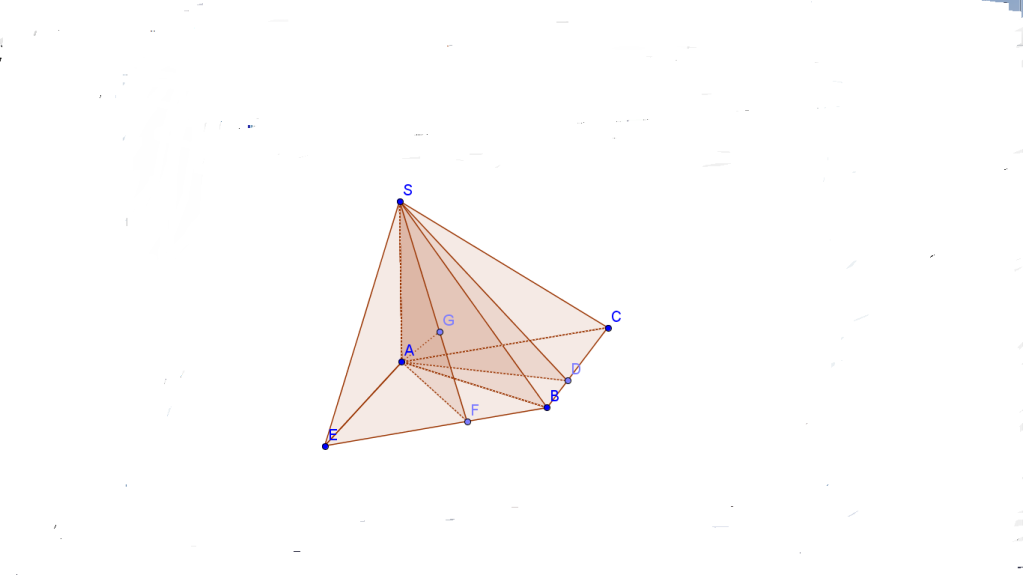
Câu IV. (1.0 điểm) Cho hình chóp $S.ABC$ có $SA$ vuông góc với đáy, $AB=a \ ; AC=2a \ ; \ \widehat{BAC}=120^0.$ Mặt phẳng $(SBC)$ tạo với đáy một góc $60^0$. Tính thể tích khối chóp $S.ABC$ và khoảng cách giữa hai đường thẳng $SB$ và $AC$ theo $a.$

Câu V. (1.0 điểm). Cho $a \ , \ b , \ c \in [1;2].$ Tìm giá trị nhỏ nhất và lớn nhất của $\ (a+b+c)\left(\dfrac{1}{a}+ \dfrac{1}{b} + \dfrac{1}{c} \right)^2$

PHẦN RIÊNG. (3.0 điểm): Thí sinh chỉ được chọn một trong hai phần (phần A hoặc phần B)

A. Theo chương chình chuẩn
Câu VIa. (2.0 điểm)
1) Trên mặt phẳng tọa độ $Oxy$ cho đường thẳng $d : 3x-y+15=0$ và hai điểm $M(-2;4) , I(0;3).$ Tìm toạ độ các đỉnh của hình thoi $ABCD$ biết $A$ nằm trên đường thẳng $d$, M là trung điểm của $AB$, $I$ là giao điểm của hai đường chéo, diện tích hình thoi bằng $16$ và $x_A <-3.$
2) Trong không gian với hệ trục tọa độ $Oxyz$ cho mặt phẳng $(P) : 2x-y+2x+6=0$ và đường thẳng $(\Delta) : \dfrac{x+1}{1}= \dfrac{y-6}{-1}= \dfrac{z+5}{2}.$ Viết phương trình đường thẳng $(d)$ đi qua $A(-3;0;2)$ và cắt $(\Delta)$ tại $B$ sao cho mặt cầu tâm $B$ tiếp xúc với hai mặt phẳng $(Oxz)$ và $(P).$

Câu VIIa. (1.0 điểm). Trong mặt phẳng toạ độ $Oxy$, tìm tập hợp các điểm $M$ biễu diễn số phức $w=2z-3i$, biết số phức $z$ thoả mãn bất đẳng thức $|z-3| \le |2z+3i-1|$
B. Theo chương trình nâng cao
Câu VIb. (2.0 điểm)
1) Trong mặt phẳng tọa độ $Oxy$ cho hai đường tròn $(C_1) : (x-1)^2 + (y - 2)^2 = 5 \ ; \ (C_2) : (x-3)^2+y^2=9$.Xét đường thẳng $d$ đi qua giao điểm $A \quad (x_A \ne 0)$ của $(C_1) \ ; \ (C_2)$ và lần lượt cắt $(C_1) \ ; \ (C_2)$ tại các giao điểm thứ hai là $B,C.$ Tìm toạ độ điểm $D$ thuộc đường thẳng $d_1 : x-y-4=0$ sao cho $\overrightarrow{BC}=2 \overrightarrow{AD}.$

2) Trong không gian với hệ trục tọa độ $Oxyz$ cho mặt cầu $(S) : (x-1)^2+(y-2)^2+(z-3)^2 = 25$ và ba điểm $A(2;3;1),B(2;3;-2),C(0;4;3)$. Gọi mặt phẳng $(P)$ đi qua $A$ và cắt $(S)$ theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Lập phương trình đường thẳng $(d)$ đi qua $B$ nằm trong mặt phẳng $(P)$ và cách $C$ một khoảng bằng $\dfrac{\sqrt{6}}{2}$.[/list]Câu VIIb. (1.0 điểm) Giải hệ phương trình sau trên $\mathbb R$ : $\ \begin{cases}x^4 - (1+x^2y^2)\log_{\frac{1}{5}}x = y^4 - (1+x^2y^2)\log_{\frac{1}{5}}y \\ x + \sqrt{2y+1}=1 + \sqrt{2x-y+2}\end{cases}$

.........................................................HẾT...............................................

Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 25-02-2012 - 12:31

[dark templar]

Àh Kiên cho anh hỏi là đề này là đề thi giống đề thi thử VMF,tức là cho thành viên làm rồi nộp phải không ? Nếu đúng thì em không nên copy qua đây,lỡ có mem nào trả lời thì hỏng mất cuộc thi của người ta

Bài viết đã được chỉnh sửa nội dung bởi dark templar: 24-02-2012 - 22:49

[Ispectorgadget]

Àh Kiên cho anh hỏi là đề này là đề thi giống đề thi thử VMF,tức là cho thành viên làm rồi nộp phải không ? Nếu đúng thì em không nên copy qua đây,lỡ có mem nào trả lời thì hỏng mất cuộc thi của người ta

À cái này giống bên boxmath đó anh. mọi người cứ thảo luận thoái mái!

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu I (2.0 điểm). Cho hàm số: $y = \dfrac{x+3}{x+1}$ có đồ thị là $(H)$
2) Cho đường tròn $©$ có phương trình $(x+1)^2+(y-1)^2=\dfrac{16}{5}.$ Tìm tất cả các điểm $M$ thuộc $©$ sao cho tiếp tuyến tại $M$ của $©$ cũng là tiếp tuyến của $(H)$

Bài này cho hay đấy
Phương trình tiếp tuyến của $(H)$ có dạng:
$$(\Delta):y=f'(x_0)(x-x_0)+f(x_0)$$
Trong đó $x_0 \neq -1$ là hoành độ tiếp điểm;$f(x)=\frac{x+3}{x+1}=1+\frac{2}{x+1}$
Hay:
$$(\Delta):y=\frac{-2(x-x_0)}{(x_0+1)^2}+1+\frac{2}{x_0+1}$$
Do $(\Delta)$ tiếp xúc với $\left(C \right)$ nên:
$$d[I;(\Delta)]=R$$
Trong đó $I(-1;1)$ và $R=\frac{4}{\sqrt{5}}$ lần lượt là tâm và bán kính của $\left(C \right)$.
$$\iff \frac{\left|\frac{2(x_0+1)}{(x_0+1)^2}+1+\frac{2}{x_0+1}-1 \right|}{\sqrt{1+\frac{4}{(x_0+1)^4}}}=\frac{4}{\sqrt{5}} \iff \frac{5}{(x_0+1)^2}=1+\frac{4}{(x_0+1)^4}(1)$$
Đặt $t=\frac{1}{(x_0+1)^2}(t>0)$ thì phương trình (1) trở thành:
$$4t^2+1-5t=0 \iff t \in \left\{\frac{1}{4};1 \right\}$$
Với $t=1$ thì $\frac{1}{(x_0+1)^2}=1 \iff x_0 \in \{0;-2 \}$.

Trường hợp 1:$x_0=0$:Phương trình $(\Delta)$ trở thành:$y=-2x+3$
Ta có điểm $M(a;b)$ phải thỏa mãn hệ phương trình sau:
$$\left\{\begin{matrix} (a+1)^2+(b-1)^2=\frac{16}{5} \\ 2a+b=3 \end{matrix}\right. \iff \left\{\begin{matrix}(a+1)^2+4(1-a)^2=\frac{16}{5} \\ b=3-2a \end{matrix}\right. \iff \left\{\begin{matrix}5a^2+6a+\frac{9}{5}=0 \\ b=3-2a \end{matrix}\right. \iff (a;b)=\left(-\frac{3}{5};\frac{21}{5} \right)$$
Vậy ta có điểm $M\left(-\frac{3}{5};\frac{21}{5} \right)$.

Trường hợp 2:$x_0=-2$:Phương trình $(\Delta)$ trở thành:$2x+y+5=0$
Cũng tương tự với TH1,ta cũng phải giải hệ sau:
$$\left\{\begin{matrix}(a+1)^2+(b-1)^2=\frac{16}{5} \\ 2a+b+5=0 \end{matrix}\right. \iff \left\{\begin{matrix}(a+1)^2+4(a+3)^2=\frac{16}{5} \\ b=-2a-5 \end{matrix}\right. \iff \left\{\begin{matrix}5a^2+26a+\frac{169}{5}=0 \\ b=-2a-5 \end{matrix}\right. \iff (a;b)=\left(-\frac{13}{5};\frac{11}{5} \right)$$
Vậy ta tiếp tục có điểm $M\left(-\frac{13}{5};\frac{11}{5} \right)$.

Với $t=\frac{1}{4}$ thì $\frac{1}{(x_0+1)^2}=\frac{1}{4} \iff x_0 \in \{1;-3 \}$.

Trường hợp 3:$x_0=1$:Phương trình $(\Delta)$ trở thành:$2y+x-5=0$
Tương tự với 2 TH trên,ta sẽ thu được điểm $M\left(\frac{-1}{5};\frac{13}{5} \right)$.

Trường hợp 4:$x_0=-3$:Phương trình $(\Delta)$ trở thành:$2y+x+3=0$
Tương tự,ta thu được điểm $M\left(\frac{-9}{5};\frac{-3}{5} \right)$.

KẾT LUẬN: Tồn tại 4 điểm $M(a;b)$ sao cho $(a;b)=\left(-\frac{3}{5};\frac{21}{5} \right);\left(-\frac{13}{5};\frac{11}{5} \right);\left(\frac{-1}{5};\frac{13}{5} \right);\left(\frac{-9}{5};\frac{-3}{5} \right)$.

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu II. (2.0 điểm)
2) Giải hệ phương trình : $\begin{cases} x + \sqrt{x^2-2x+5} =3y + \sqrt{y^2+4}(1) \\ x^2-y^2-3x+3y+1=0(2) \end{cases}$

Cộng vế theo vế của (1) và (2),ta thu được:
$$x+\sqrt{x^2-2x+5}+x^2-y^2-3x+3y+1=3y+\sqrt{y^2+4} \iff (x-1)^2+\sqrt{(x-1)^2+4}=y^2+\sqrt{y^2+4}(3)$$
Xét hàm số $f(t)=t+\sqrt{t+4}(t \ge 0)$
$f'(t)=1+\frac{1}{2\sqrt{t+4}}>0,\forall t \ge 0$
Suy ra:$f(t)$ đồng biến trên $[0;+\infty)$.
Mà ta lại có:$(3) \iff f((x-1)^2)=f(y^2)$ nên ta thu được:$(x-1)^2=y^2 \iff x-1=y$ hay $x-1=-y$

Trường hợp 1:$x-1=y$.Thay vào (2),ta có:$x=\frac{3}{2} \Rightarrow y=\frac{1}{2}$
Trường hợp 2:$x-1=-y$.Thay vào (2),ta có:$x=\frac{3}{4} \Rightarrow y=\frac{1}{4}$

Vậy hệ phương trình có nghiệm là:$(x;y)=\left(\frac{3}{2};\frac{1}{2} \right);\left(\frac{3}{4};\frac{1}{4} \right)$.

[Ispectorgadget]

Tìm giá trị nhỏ nhất:
Theo bất đẳng thức $AM-GM$ ta có: $(a+b+c)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\geq 9\Rightarrow \left(\dfrac{1}{a}+ \dfrac{1}{b}+ \dfrac{1}{c} \right)^2\geq \dfrac{81}{(a+b+c)^2}$
Suy ra: $\ P\geq \dfrac{81}{a+b+c}$
Mặt khác ta có: $\ a+b+c\leq 6\Rightarrow P\geq \dfrac{81}{6}=\dfrac{27}{2}$. Dấu $''=''$ xảy ra khi $a=b=c=2$
Vậy $ \ Pmin=\dfrac{27}{2}$

Tìm giá trị lớn nhất

Đặt $\dfrac{1}{a}=x; \ \dfrac{1}{b}=y; \dfrac{1}{c}=z\Rightarrow x, \ y, \ z\in\left[\dfrac{1}{2}; \ 1\right]$

Ta viết lại: $\ P=(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z})(x+y+z)^2 $
Không mất tính tổng quát ta có thể giả sử: $x\geq y\geq z$
$-$ Xét hàm số: $\ f(x)=(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z})(x+y+z)^2$ (coi $x$ là biến) với $x, \ y, \ z\in\left[\dfrac{1}{2}; \ 1\right]$

Ta có: $ \ f'(x)=-\dfrac{1}{x^2}(x+y+z)^2+2(x+y+z)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=(x+y+z)\left( \dfrac{xyz+2x^2(y+z)-yz(y+z)}{x^2yz}\right)>0$ (Do $x^2\geq yz$)

Như vậy hàm số $f(x)$ đồng biến. Suy ra $f(x)\leq f(1)=\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)(1+y+z)^2=g(y)$

$-$ Coi $y$ là ẩn ta xét hàm số $\ g(y)=\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)(1+y+z)^2$

Lại có: $\ g'(y)=-\dfrac{1}{y^2}(1+y+z)^2+2(1+y+z)\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{1+y+z}{y^2z}(2y^2(z+1)+zy-z-z^2)$

Xét tam thức bậc $2$, $\ t(y)=2y^2(z+1)+zy-z-z^2$
Có $t(y)=0\Leftrightarrow \left[\begin{array}{l}y=\dfrac{-z+\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\\y=\dfrac{-z-\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\end{array}\right.$

Mặt khác ta dễ chứng minh: $\ y=\dfrac{-z+\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\leq \dfrac{1}{2}$. Điều này tương đương với $19z^2+40z+16-8z^3>0$ (hiển nhiên đúng với $z\in\left[\dfrac{1}{2};\ 1\right]$

Suy ra $t(y)>0$ với mọi $y\in\left[\dfrac{1}{2};\ 1\right]$

Suy ra $\ g'(y)>0\Rightarrow g(y)\leq g(1)=\left(2+\dfrac{1}{z}\right)(2+z)^2=h(z)$

$-$ Cuối cùng ta dễ dàng kiểm tra được $h(z)-27=\left(2+\dfrac{1}{z}\right)(2+z)^2-27=\dfrac{(z-1)(2z^2+11z-4)}{z}\leq 0$

Vậy $P\leq 27$. Khi $x=y=z=1\Leftrightarrow a=b=c=1$ thì $P=27$
Do đó $P \ max=27 $

Nguồn: onluyentoan.vn

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu II. (2.0 điểm)
1) Giải phương trình lượng giác : $\dfrac{\cos^2 x-4}{3+4\sin x -\cos 2x}=\cot^2 \left(\dfrac{x}{2} + \dfrac{\pi}{4} \right)\left(\dfrac{1}{2} - \sin x \right)$

Giải nốt luôn câu lượng giác
ĐKXĐ:$\left\{\begin{matrix}3+4\sin{x}-\cos{2x} \neq 0 \\ \sin^2{\left ( \frac{x}{2}+\frac{\pi}{4} \right )} \neq 0 \end{matrix}\right. \iff \left\{\begin{matrix}2(\sin{x}+1)^2 \neq 0 \\ \sin{\left ( \frac{x}{2}+\frac{\pi}{4} \right )} \neq 0 \end{matrix}\right. \iff x \neq \frac{-\pi}{2}+k2\pi(k \in \mathbb{Z})$
Sử dụng công thức hạ bậc và $\cos{2y}=1-2\sin^2{y}$,ta có phương trình ban đầu tương đương với:
$$\frac{\cos^2{x}-4}{3+4\sin{x}-(1-2\sin^2{x})}=\frac{\cos^2{\left(\frac{x}{2}+\frac{\pi}{4} \right)}}{\sin^2{\left(\frac{x}{2}+\frac{\pi}{4} \right)}}\left(\frac{1}{2}-\sin{x} \right) \iff \frac{\cos^2{x}-4}{2(\sin{x}+1)^2}=\frac{1+\cos{\left(x+\frac{\pi}{2} \right)}}{1-\cos{\left(x+\frac{\pi}{2} \right)}}\left(\frac{1}{2}-\sin{x} \right)$$
$$\iff \frac{\cos^2{x}-4}{(\sin{x}+1)^2}=\frac{1-\sin{x}}{1+\sin{x}}(1-2\sin{x}) \iff \cos^2{x}-4=(1-\sin^2{x})(1-2\sin{x})$$
$$\iff 2\cos^2{x}\sin{x}=4 \iff \sin^3{x}-\sin{x}+2=0(1)$$
Ta có:$\left\{\begin{matrix}1-\sin{x} \ge 0\\ \sin^3{x}+1 \ge 0 \end{matrix}\right.\Rightarrow \sin^3{x}-\sin{x}+2 \ge 0$.
Nhưng dấu đẳng thức không thể đồng thời xảy ra nên phương trình (1) vô nghiệm.Suy ra phương trình ban đầu vô nghiệm.

Bài viết đã được chỉnh sửa nội dung bởi dark templar: 25-02-2012 - 21:44

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu III. (1.0 điểm). Tính $I=\displaystyle \int _{0}^{1} \dfrac{1+(2+x)xe^{2x}}{1+xe^x}\mbox{d}x$

$$I=\int_{0}^{1}\left(xe^{x}+2e^{x}+1-\frac{2e^{x}(x+1)}{xe^{x}+1} \right)dx=(e^{x}(x-1))\Big|_{0}^{1}+2e^{x}\Big|_{0}^{1}+x\Big|_{0}^{1}-2\int_{0}^{1}\frac{d(xe^{x}+1)}{xe^{x}+1}$$
$$=1+2(e-1)+1-2\ln{|xe^{x}+1|}\Big|_{0}^{1}=2e-2\ln{(e+1)}$$

Bài viết đã được chỉnh sửa nội dung bởi dark templar: 26-02-2012 - 07:49

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN RIÊNG. (3.0 điểm): Thí sinh chỉ được chọn một trong hai phần (phần A hoặc phần B)

A. Theo chương chình chuẩn
Câu VIIa. (1.0 điểm). Trong mặt phẳng toạ độ $Oxy$, tìm tập hợp các điểm $M$ biễu diễn số phức $w=2z-3i$, biết số phức $z$ thoả mãn bất đẳng thức $|z-3| \le |2z+3i-1|$

Thay $z=\frac{w+3i}{2}$,ta thu được:
$$\left|\frac{w+3i-6}{2} \right| \le |w+6i-1|(1)$$
Đặt $w=a+bi(a,b \in \mathbb{R})$,ta có:
$$(1) \iff \left|\frac{a-6}{2}+\frac{b+3}{2}i \right| \le |a-1+(b+6)i| \iff \sqrt{\frac{(a-6)^2}{4}+\frac{(b+3)^2}{4}} \le \sqrt{(a-1)^2+(b+6)^2} \iff \left(a+\frac{2}{3} \right)^2+(b+7)^2 \ge \frac{148}{9}$$
Như vậy,tập hợp điểm M là toàn bộ mặt phẳng $Oxy$ bỏ đi phần hình tròn(không lấy đường tròn) có tâm $I\left(\frac{-2}{3};-7 \right)$ và bán kính $R=\frac{2\sqrt{37}}{3}$.

[Tham Lang]

Tìm giá trị nhỏ nhất:
Theo bất đẳng thức $AM-GM$ ta có: $(a+b+c)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\geq 9\Rightarrow \left(\dfrac{1}{a}+ \dfrac{1}{b}+ \dfrac{1}{c} \right)^2\geq \dfrac{81}{(a+b+c)^2}$
Suy ra: $\ P\geq \dfrac{81}{a+b+c}$
Mặt khác ta có: $\ a+b+c\leq 6\Rightarrow P\geq \dfrac{81}{6}=\dfrac{27}{2}$. Dấu $''=''$ xảy ra khi $a=b=c=2$
Vậy $ \ Pmin=\dfrac{27}{2}$

Tìm giá trị lớn nhất

Đặt $\dfrac{1}{a}=x; \ \dfrac{1}{b}=y; \dfrac{1}{c}=z\Rightarrow x, \ y, \ z\in\left[\dfrac{1}{2}; \ 1\right]$

Ta viết lại: $\ P=(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z})(x+y+z)^2 $
Không mất tính tổng quát ta có thể giả sử: $x\geq y\geq z$
$-$ Xét hàm số: $\ f(x)=(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z})(x+y+z)^2$ (coi $x$ là biến) với $x, \ y, \ z\in\left[\dfrac{1}{2}; \ 1\right]$

Ta có: $ \ f'(x)=-\dfrac{1}{x^2}(x+y+z)^2+2(x+y+z)\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)=(x+y+z)\left( \dfrac{xyz+2x^2(y+z)-yz(y+z)}{x^2yz}\right)>0$ (Do $x^2\geq yz$)

Như vậy hàm số $f(x)$ đồng biến. Suy ra $f(x)\leq f(1)=\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)(1+y+z)^2=g(y)$

$-$ Coi $y$ là ẩn ta xét hàm số $\ g(y)=\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)(1+y+z)^2$

Lại có: $\ g'(y)=-\dfrac{1}{y^2}(1+y+z)^2+2(1+y+z)\left(1+\dfrac{1}{y}+\dfrac{1}{z}\right)=\dfrac{1+y+z}{y^2z}(2y^2(z+1)+zy-z-z^2)$

Xét tam thức bậc $2$, $\ t(y)=2y^2(z+1)+zy-z-z^2$
Có $t(y)=0\Leftrightarrow \left[\begin{array}{l}y=\dfrac{-z+\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\\y=\dfrac{-z-\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\end{array}\right.$

Mặt khác ta dễ chứng minh: $\ y=\dfrac{-z+\sqrt{z^2+8z(z+1)^2}}{4(z+1)}\leq \dfrac{1}{2}$. Điều này tương đương với $19z^2+40z+16-8z^3>0$ (hiển nhiên đúng với $z\in\left[\dfrac{1}{2};\ 1\right]$

Suy ra $t(y)>0$ với mọi $y\in\left[\dfrac{1}{2};\ 1\right]$

Suy ra $\ g'(y)>0\Rightarrow g(y)\leq g(1)=\left(2+\dfrac{1}{z}\right)(2+z)^2=h(z)$

$-$ Cuối cùng ta dễ dàng kiểm tra được $h(z)-27=\left(2+\dfrac{1}{z}\right)(2+z)^2-27=\dfrac{(z-1)(2z^2+11z-4)}{z}\leq 0$

Vậy $P\leq 27$. Khi $x=y=z=1\Leftrightarrow a=b=c=1$ thì $P=27$
Do đó $P \ max=27 $

Nguồn: onluyentoan.vn

Bài này tìm min thì dễ rồi, nhưng max làm như thế này tuy hay nhưng quá dài.
$$(a - 1)(a - 2) \le 0 \Leftrightarrow a + \dfrac{2}{a} \le 3$$
Lại có $$\left (a + b + c\right )\left (\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \right )^2 \le \dfrac{\left (a + b + c + \dfrac{2}{a} + \dfrac{2}{b} + \dfrac{2}{c} \right )}{27} \le \dfrac{9^3}{27} = 27$$

Bài viết đã được chỉnh sửa nội dung bởi huymit_95: 26-02-2012 - 09:28

[dark templar]

ĐỀ THI THỬ ĐẠI HỌC SỐ 3 CỦA DIỄN ĐÀN ONLUYENTOAN.VN
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm):
Câu IV. (1.0 điểm) Cho hình chóp $S.ABC$ có $SA$ vuông góc với đáy, $AB=a \ ; AC=2a \ ; \ \widehat{BAC}=120^0.$ Mặt phẳng $(SBC)$ tạo với đáy một góc $60^0$. Tính thể tích khối chóp $S.ABC$ và khoảng cách giữa hai đường thẳng $SB$ và $AC$ theo $a.$

Làm luôn câu hình Không gian cho hết phần thi chung

Kẻ $AD \perp BC(D \in BC)$.Ta có:
$$\left\{\begin{matrix} SA \perp (ABC)\Rightarrow BC \perp SA \\ BC \perp AD;AD,BC \in (SAD) \end{matrix}\right. \Rightarrow BC \perp (SAD) \Rightarrow SD \perp BC$$
Như vậy:
$$\widehat{((SBC);(ABC))}=60^0=\widehat{(AD;SD)}=\widehat{SDA}$$
Theo định lý hàm số cosin,ta có:
$$\cos{\widehat{BAC}}=\cos{120^0}=-\frac{1}{2}=\frac{AB^2+AC^2-BC^2}{2AB.AC} \Rightarrow BC=a\sqrt{6}$$
Lại có:
$$S_{ABC}=\frac{1}{2}AB.AC\sin{\widehat{BAC}}=\frac{\sqrt{3}a^2}{2}=\frac{1}{2}AD.BC$$
Suy ra:$AD=\frac{a}{\sqrt{2}} \Rightarrow SA=\sin{\widehat{SDA}}.AD=\sin{60^0}.\frac{a}{\sqrt{2}}=\frac{\sqrt{3}a}{2\sqrt{2}}$.
$\Rightarrow V_{S.ABC}=\frac{1}{3}.SA.S_{ABC}=\frac{1}{3}.\frac{\sqrt{3}a}{2\sqrt{2}}.\frac{\sqrt{3}a^2}{2}=\frac{a^3}{4\sqrt{2}}$
Dựng hình bình hành ACBE.Kẻ $AF \perp BE(F \in BE);AG \perp SF(G \in SF)$.Ta có:
$$\left\{\begin{matrix}BE \perp AF \\ SA \perp (ACBE) \Rightarrow AF \perp SA \\ SA,AF \in (SAF) \end{matrix}\right. \Rightarrow BE \perp (SAF) \Rightarrow BE \perp AG$$.
Lại có:
$$\left\{\begin{matrix}AG \perp BE \\ AG \perp SF \\ BE,SF \in (SBE) \end{matrix}\right. \Rightarrow d[A;(SBE)]=AG$$
Mặt khác:
$$AC//BE \Rightarrow d[AC;SB]=d[A;(SBE)]=AG$$
Có:$AF=\frac{2S_{ABE}}{BE}=\frac{2S_{ABC}}{AC}=\frac{\sqrt{3}a^2}{2a}=\frac{\sqrt{3}a}{2}$.
Suy ra:
$$AG=\frac{SA.AF}{\sqrt{SA^2+AF^2}}=\frac{a}{2}$$.