Việt Nam Team Selection Test 2012 - Đề bài, lời giải và danh sách đội tuyển
#1
 Đã gửi 15-04-2012 - 21:56
Đã gửi 15-04-2012 - 21:56

Mình mở topic này để mọi người post đề bài, thảo luận về kì thi này. Vậy, mai ai có đề thì gõ Latex sạch đẹp và viết lên #2 nhé, chú ý là #2 chỉ để post đề bài, vi phạm thì mình buộc phải xoá.
- Ispectorgadget, Zaraki, Tham Lang và 7 người khác yêu thích
#2
 Đã gửi 16-04-2012 - 16:03
Đã gửi 16-04-2012 - 16:03

Ngày thi thứ nhất
Thời gian: 270 phút
Bài 1 (7 điểm)
Cho đường tròn $(O)$ và 2 điểm cố định $B,C$ trên đường tròn sao cho $BC$ không là đường kính của $(O)$, $A$ là một điểm di động trên đường tròn, $A$ không trùng với $B,C$. Gọi $D,K,J$ lần lượt là trung điểm của $BC,CA,AB$ và $E,M,N$ lần lượt là hình chiếu vuông góc của $A,B,C$ trên $BC, DJ, DK$. Các tiếp tuyến tại $M,N$ của đường tròn ngoại tiếp tam giác $EMN$ cắt nhau tại $T$. Chứng minh $T$ là điểm cố định.
Bài 2 (7 điểm)
Trên một cánh đồng hình chữ nhật kích thước $m\times n$ ô vuông gồm $m$ hàng và $n$ cột người ta đặt một số máy bơm nước vào các ô vuông. Biết rằng mỗi máy bơm nước có thể tưới nước cho các ô vuông có chung cạnh với nó và các ô vuông cùng cột với nó và cách nó đúng một ô vuông . Tìm số nhỏ nhất các máy bơm nước sao cho các máy bơm nước có thể tưới hết cả cánh đồng trong 2 trường hợp:
a) $m=4$
b) $m=3$
Bài 3 (7 điểm)
Cho số nguyên tố $p\ge 17$. Chứng minh rằng $t=3$ là số nguyên dương lớn nhất thỏa mãn điều kiện: Với các số nguyên bất kì $a,b,c,d$ sao cho $abc$ không chia hết cho $p$ và $a+b+c$ chia hết cho $p$ thì tồn tại các số nguyên $x,y,z$ thuộc tập $\{0;1;...;\left[\frac{p}{t}\right]-1\}$ sao cho $ax+by+cz+d\vdots p$
Ngày thi thứ 2
Bài 4: (7 điểm)
Cho dãy số $(x_n)$ xác định bởi $x_1=1,x_2=2011$ và $x_{n+2}=4022x_{n+1}-x_n,\forall n\in \mathbb N$.
Chứng minh rằng $\frac{x_{2012}+1}{2012}$ là số chính phương.
Bài 5: (7 điểm)
Chứng minh rằng $c=10\sqrt{24}$ là hằng số lớn nhất thỏa mãn điều kiện: nếu có các số dương $a_1,a_2,...a_{17}$ sao cho: $$\sum_{i=1}^{17}{a_i^2}=24\qquad ;\qquad \sum_{i=1}^{17}{a_i^3}+\sum_{i=1}^{17}{a_i}<c$$ Thì với mọi $i,j,k$ thỏa mãn $1\le i<j<k\le 17$, ta luôn có $a_i,a_j,a_k$ là độ dài ba cạnh của một tam giác.
Bài 6: (7 điểm)
Có 42 học sinh tham dự kì thi chọn đội tuyển Olympic toán quốc tế. Biết rằng một học sinh bất kì quen đúng 20 học sinh khác. Chứng minh rằng ta có thể chia 42 học sinh thành 2 nhóm hoặc 21 nhóm sao cho số học sinh trong các nhóm bằng nhau và 2 học sinh bất kì trong cùng nhóm thì quen nhau.
(Cuối giờ ban tổ chức đã thu lại hết đề nên đây chỉ là đề mình ghi lại, không phải nguyên văn
Bài viết đã được chỉnh sửa nội dung bởi hoangduc: 17-04-2012 - 16:57
- anh qua, NguyThang khtn, đat và 14 người khác yêu thích
HỌC, HỌC NỮA, HỌC MÃI
#3
 Đã gửi 16-04-2012 - 16:52
Đã gửi 16-04-2012 - 16:52

rút cục chả làm được gì
ngày mai chắc cũng thế nốt
hình như có mỗi bạn ở Cần Thơ, ngày mai làm quen phát
Bài viết đã được chỉnh sửa nội dung bởi PTH_Thái Hà: 16-04-2012 - 16:54
- Tham Lang yêu thích
#4
 Đã gửi 16-04-2012 - 20:12
Đã gửi 16-04-2012 - 20:12

kq câu a là n máy bơm.
Câu b đáp số của mình nếu $n=4k$ thì số máy bơm cần có là $3k+1$ còn nếu $n \ne 4k$ thì số máy bơm tối thiểu là $n-\lfloor \frac{n}{4} \rfloor$
Bài viết đã được chỉnh sửa nội dung bởi Karl Heinrich Marx: 16-04-2012 - 23:06
- alex_hoang yêu thích
#5
 Đã gửi 16-04-2012 - 21:28
Đã gửi 16-04-2012 - 21:28

Những ngày cuối cùng còn học toán
winwave1995
#6
 Đã gửi 16-04-2012 - 21:43
Đã gửi 16-04-2012 - 21:43

Bạn có thể minh họa hình vẽ được khôngcâu a hình như bạn ko đúng thì phải. Ý tưởng của mình là thế này ko bik đúng ko. Ta tô theo hình zich zắc. Theo kiểu đường chéo của hình vuông 3x3 thì thấy. Một vòi nước chỉ có thể tưới nhiều nhất 2 ô trong số các ô ta đã tô. Ví dụ với n=7 thì ta cần 4 vòi nước. Mình biện luận ra với n=6k+1 thì có ít nhất T=3k+1, với n=6k+2 thì có ít nhất T+1, n=6k+3 và 6k+4 thì có đáp số là T+2, n=6k+5 và 6k+6 thì có T+3. Còn với câu b mình có đáp số là kq câu a cộng thêm với $[\frac{n}{6}+1]$
#7
 Đã gửi 16-04-2012 - 21:54
Đã gửi 16-04-2012 - 21:54

Những ngày cuối cùng còn học toán
winwave1995
#8
 Đã gửi 16-04-2012 - 23:06
Đã gửi 16-04-2012 - 23:06

#9
 Đã gửi 16-04-2012 - 23:12
Đã gửi 16-04-2012 - 23:12

đặt
\[\left[ {\frac{p}{t}} \right] - 1 = k;y - x = u;z - x = v\]
Với t>3 thì cho b=c ,ta cần chứng minh b(m+n) tạo thành hệ thặng dư module p
Mặt khác m+n chạy từ -2k đến 2k, tức là có 4k+1 số m+n module p => 4k+1 số b(m+n) module p
mà với t>3 thì 4k+1<p, vô lý.
với t=3
thì ta cần c/m luôn tồn tại m;n thuộc khoảng [-k;k] để
\[bu + cv \equiv d\left( {\bmod p} \right)\forall d \in \left[ {0;p - 1} \right]\]
Lại có u thuộc khoảng [-k;k] nên có 2k+1 số u, tức là có 2k+1 số bu khác nhau module p
=> có 2k+1 số d-bu khác nhau module p,
và có 2k+1 số cv khác nhau module p
mặt khác 4k+2>p với t=3;p>13 nên sẽ tồn tại 2 số bằng nhau (dirichle), tức là d-bu=cv hay d=bu+cv(modulo p)
ta có điều phải chứng minh
- hoangduc, NguyThang khtn, perfectstrong và 2 người khác yêu thích

#10
 Đã gửi 16-04-2012 - 23:27
Đã gửi 16-04-2012 - 23:27

Những ngày cuối cùng còn học toán
winwave1995
#11
 Đã gửi 17-04-2012 - 00:49
Đã gửi 17-04-2012 - 00:49

Kí hiệu $(XY)$ chỉ đường tròn đường kính $(XY).$
Gọi$M', N'$theo thứ tự là hình chiếu của $B, C $trên $AC, AB. H$ là trực tâm tam giác $ABC$ Ta có các bộ điểm thẳng hàng $(B, M, H, M') (C, N, H, N').$Dễ thấy$ D, M, H, N $đồng viên.
$X$ là hình chiếu của $H$trên $AD.$ Khi đó,$X$ thuộc $(HA), (HD).$
Xét 3 đường tròn $(BC), (HA), (HD)$ có các trục đẳng phương $M'N', XH, BC $đồng quy tại $I.$
Chú ý rẳng $AE, BM', CN' $đồng quy do đó $(BCDI)= -1$. Qua phép chiếu xuyên tâm H ta có $H(MNDX)=-1$nên tứ giác $MDNX$điều hòa suy ra$ X, E, T$thẳng hàng.
Gọi $S$ là giao điểm của$OD$và$(HD)$ ta có $HS$ song song với $BC$và $D$ là trung điểm $BC$ suy ra $H(SDBC)=-1$ hay $H(SDMN)=-1$. Do đó $DMSN$điều hòa suy ra $S, T, D$thẳng hàng.
Dề thấy (bằng cộng góc)$ DM' $là tiếp tuyến của $(HA)$ dó đó $DC^2=DM'^2=DX.DA.$
Các tam giác$AEX $và $ADH$đồng dạng nên ta có $\frac{AE}{XA}=\frac{AD}{HA}$Ta có $TD$song song với$AH.$Vì thế theo định lý Thales ta có $\frac{DT}{DX}=\frac{AE}{AX}$ suy ra [$DT=DX.\frac{AE}{AX}=DX.\frac{DA}{AH}=\frac{DA.DX}{AH}=\frac{DC^2}{2OD}$không đổi.
Vậy$T$ là điểm cố định
Bài viết đã được chỉnh sửa nội dung bởi alex_hoang: 17-04-2012 - 00:57
- perfectstrong yêu thích
#12
 Đã gửi 17-04-2012 - 12:15
Đã gửi 17-04-2012 - 12:15

Anh ơi, $m,n$ là gì trong bài này hả anh?\[{\rm{ax}} + by + cz = x(a + b + c) + b(y - x) + c(z - x)\]
đặt
\[\left[ {\frac{p}{t}} \right] - 1 = k;y - x = u;z - x = v\]
Với t>3 thì cho b=c ,ta cần chứng minh b(m+n) tạo thành hệ thặng dư module p
Mặt khác m+n chạy từ -2k đến 2k, tức là có 4k+1 số m+n module p => 4k+1 số b(m+n) module p
mà với t>3 thì 4k+1<p, vô lý.
với t=3
thì ta cần c/m luôn tồn tại m;n thuộc khoảng [-k;k] để
\[bu + cv \equiv d\left( {\bmod p} \right)\forall d \in \left[ {0;p - 1} \right]\]
Lại có u thuộc khoảng [-k;k] nên có 2k+1 số u, tức là có 2k+1 số bu khác nhau module p
=> có 2k+1 số d-bu khác nhau module p,
và có 2k+1 số cv khác nhau module p
mặt khác 4k+2>p với t=3;p>13 nên sẽ tồn tại 2 số bằng nhau (dirichle), tức là d-bu=cv hay d=bu+cv(modulo p)
ta có điều phải chứng minh
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
#13
 Đã gửi 17-04-2012 - 14:28
Đã gửi 17-04-2012 - 14:28

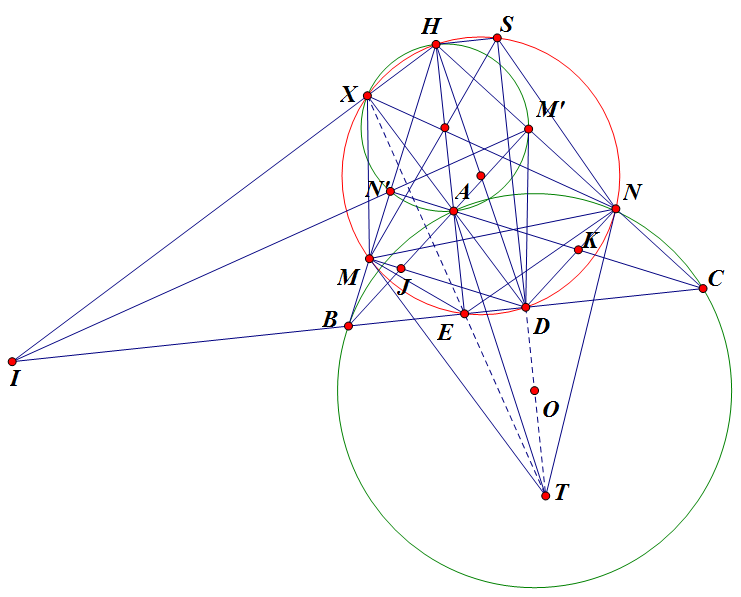
Em sửa lại chút (theo ý em là đúng) và up cái hình.Kí hiệu $(XY)$ chỉ đường tròn đường kính $(XY).$
Gọi $M', N'$ theo thứ tự là hình chiếu của $B, C $trên $AC, AB$. $H$ là trực tâm $\vartriangle ABC$
Ta có các bộ điểm thẳng hàng $(B, M, H, N') (C, N, H, M').$Dễ thấy$ D, M, H, N $đồng viên.
$X$ là hình chiếu của $H$ trên $AD$. Khi đó,$X$ thuộc $(HA), (HD).$
Xét 3 đường tròn $(BC), (HA), (HD)$ có các trục đẳng phương $M'N', XH, BC $đồng quy tại $I$.
Chú ý rẳng $AE, BM', CN' $đồng quy do đó $(BCEI)= -1$. Qua phép chiếu xuyên tâm H ta có $H(MNEX)=-1$nên tứ giác $MENX$điều hòa suy ra$ X, E, T$thẳng hàng.
Gọi $S$ là giao điểm của $OD$và $(HD)$ ta có $HS \parallel BC$và $D$ là trung điểm $BC$ suy ra $H(SDBC)=-1$ hay $H(SDMN)=-1$. Do đó $DMSN$điều hòa suy ra $S, T, D$thẳng hàng.
Dề thấy (bằng cộng góc) $ DM' $ là tiếp tuyến của $(HA)$ dó đó $DC^2=DM'^2=DX.DA.$
$\vartriangle AEX \sim \vartriangle ADH \Rightarrow \frac{AE}{XA}=\frac{AD}{HA}$
Ta có $TD \parallel AH$. Vì thế theo định lý Thales ta có $\frac{DT}{DX}=\frac{AE}{AX}$
$\Rightarrow DT=DX.\frac{AE}{AX}=DX.\frac{DA}{AH}=\frac{DA.DX}{AH}=\frac{DC^2}{2OD}$không đổi.
Vậy$T$ là điểm cố định
- alex_hoang yêu thích
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
#14
 Đã gửi 17-04-2012 - 18:37
Đã gửi 17-04-2012 - 18:37

alex_hoang:hỏi chúa bạn ơi
Bài viết đã được chỉnh sửa nội dung bởi alex_hoang: 17-04-2012 - 18:48
- alex_hoang yêu thích
#15
 Đã gửi 17-04-2012 - 19:19
Đã gửi 17-04-2012 - 19:19

Đặt $a_i=\sqrt{24}x_i,$ khi đó yêu cầu bài toán tương đương với: Chứng minh rằng $C=10$ là hằng số lớn nhất sao cho nếu có $17$ số thực dương $x_1,\,x_2,\, \ldots,\, x_{17}$ thỏa mãn $$x_1^2+x_2^2+\cdots +x_{17}^2=1$$ và $$24(x_1^3+x_2^3+\cdots +x_{17}^3)+(x_1+x_2+\cdots +x_{17}) <C$$ thì với mọi $i,\, j,\, k$ thỏa mãn $1 \le i <j<k\le 17,$ ta có $x_i,\, x_j,\, x_k$ là độ dài ba cạnh của một tam giác.
Trước hết, ta sẽ chứng minh yêu cầu bài toán thỏa với $C=10.$ Không mất tính tổng quát, ta chỉ cần chứng minh $x_1,\,x_2,\, x_3$ là độ dài ba cạnh của một tam giác. Để ý rằng với mọi $0<t<1,$ ta có $$24t^3+t -(16t^4+9t^2)=t(1-t)(4t-1)^2 \ge 0.$$ Do đó, từ giả thiết ta suy ra $$16(x_1^4+x_2^4+\cdots +x_{17}^4)+9(x_1^2+x_2^2+\cdots +x_{17}^2) <10,$$ hay $$16(x_1^4+x_2^4+\cdots +x_{17}^4)<1=(x_1^2+x_2^2+\cdots +x_{17}^2)^2.$$ Bây giờ, sử dụng bất đẳng thức Cauchy-Schwarz, ta có $$16(x_1^4+x_2^4+\cdots +x_{17}^4)=\left(2+\underset{14 \text{ số}}{\underbrace{1+1+\cdots +1}}\right)\left[(x_1^4+x_2^4+x_3^4)+(x_4^4+x_5^4+\cdots +x_{17}^4)\right] \ge \left[ \sqrt{2(x_1^4+x_2^4+x_3^4)}+x_4^2+x_5^2+\cdots +x_{17}^2\right]^2.$$ Do đó, kết hợp với trên, ta thu được $$\sqrt{2(x_1^4+x_2^4+x_3^4)} <x_1^2+x_2^2+x_3^2,$$ hay $$2(x_1^4+x_2^4+x_3^4)<(x_1^2+x_2^2+x_3^2)^2.$$ Mặt khác, ta có đồng nhất thức $$\begin{aligned} (x_1^2+x_2^2+x_3^2)^2&- 2(x_1^4+x_2^4+x_3^4)= \\ &=2(x_1+x_2+x_3)(x_1+x_2-x_3)(x_2+x_3-x_1)(x_3+x_1-x_2). \end{aligned} $$ Do vậy, kết hợp với bất đẳng thức ở trên, ta suy ra $x_1,\,x_2,\,x_3$ là độ dài ba cạnh của một tam giác.
Phần chứng minh $10$ là hằng số lớn nhất khá dễ nên xin dành lại cho bà con. Giờ mình phải đi dạy tiếp đây.
Bài viết đã được chỉnh sửa nội dung bởi toanhocmuonmau: 17-04-2012 - 19:48
- hoangduc, PTH_Thái Hà, NguyThang khtn và 16 người khác yêu thích
The love makes us stronger!
V. Q. B. Can
#16
 Đã gửi 17-04-2012 - 20:07
Đã gửi 17-04-2012 - 20:07

Cho em hỏi hướng tư duy bào này được không?
- Cuong Ngyen yêu thích
It is difficult to say what is impossible, for the dream of yesterday is the hope of today and the reality of tomorrow
#17
 Đã gửi 17-04-2012 - 20:41
Đã gửi 17-04-2012 - 20:41

Mình thử chém thử bài 1 ngày hai coi sao
Trước hết ta xét phương trình
$$x^2-4022x+1=0$$
Phương trình này có hai nghiệm phân biệt là $x=2011 \pm \sqrt {{{2011}^2} - 1} $
Vậy ta tìm được công thức tổng quát cho dãy số trên là
\[{x_n} = \frac{1}{2}\left[ {{{\left( {2011 + \sqrt {{{2011}^2} - 1} } \right)}^{n - 1}} + {{\left( {2011 - \sqrt {{{2011}^2} - 1} } \right)}^{n - 1}}} \right]\]
Mà ta chú ý rằng
\[2011 \pm \sqrt {{{2011}^2} - 1} = {\left( {\sqrt {1006} \pm \sqrt {1005} } \right)^2}\]
Từ đây ta có
\[\frac{{{x_n} + 1}}{{2012}} = \frac{1}{{2.2012}}{\left[ {{{\left( {\sqrt {1006} + \sqrt {1005} } \right)}^{n - 1}} + {{\left( {\sqrt {1006} - \sqrt {1005} } \right)}^{n - 1}}} \right]^2}\]
Vậy thì
\[\frac{{{x_n} + 1}}{{2012}} = {\left[ {\frac{{{{\left( {\sqrt {1006} + \sqrt {1005} } \right)}^{n - 1}} + {{\left( {\sqrt {1006} - \sqrt {1005} } \right)}^{n - 1}}}}{{2\sqrt {1006} }}} \right]^2}\]
Ta dễ chứng minh được biểu thức
\[\frac{{{{\left( {\sqrt {1006} + \sqrt {1005} } \right)}^{n - 1}} + {{\left( {\sqrt {1006} - \sqrt {1005} } \right)}^{n - 1}}}}{{2\sqrt {1006} }}\]
Đạt giá trị nguyên khi và chỉ khi $n$ đạt giá trị chẵn và $\ge 2$
Vậy thì nó cũng đúng với $n=2012$
Mình không dự đoán trước được dãy nên làm cách củ chuối này mong mọi người thông cảm vì khả năng có hạn
- hoangduc, perfectstrong, Trần Đức Anh @@ và 2 người khác yêu thích
#18
 Đã gửi 17-04-2012 - 20:53
Đã gửi 17-04-2012 - 20:53

Bài 4 mình đang thử chứng minh bài toán tổng quát hơn là:
Cho p là số nguyên tố lẻ. Xét dãy số $(x_n)$xác định bởi:
$$x_1=1,x_2=p,x_{n+2}=2px_{n+1}-x_n, n \ge 1$$
Chứng minh rằng $\frac{x_{p+1}+1}{p+1}$ là số chính phương.
Thử với $p=3,5$ thì đúng rồi.
Em thử xem nào: $x_{n+2}=2p(2px_n - x_{n-1})-x_n=(4p^2-2)x_n-x_{n-2}$
Xét dãy $(y_n): y_1=1;y_2=2p-1; y_{n+1}=2py_n-y_{n-1}$
Ta chứng minh bằng quy nạp rằng $(p+1)(y_n)^2+1=x_{2n}$
Thật vậy, từ cách cho $y_n$ có
$y_n^2-y_{n-1}y_{n+1}=2-2p$
$(y_{n+1}+y_{n-1})^2=4p^2y_n^2\Rightarrow y_{n+1}^2=4p^2y_n^2-y_{n-1}^2-2y_{n-1}y_{n+1}=(4p^2-2)y_n^2-y_{n-1}^2 -2(2p-2)\Rightarrow y_{n+1}=\frac{(4p^2-2)(x_{2n}+1)}{p+1}-\frac{x_{2n-2}+1}{p+1}+2(2-2p)=\frac{x_{2n+2}+1}{p+1}$
Suy ra $\frac{x_{2n}+1}{p+1}$ chính phương với mọi n, p lẻ nên có đpcm.
- perfectstrong yêu thích
#19
 Đã gửi 17-04-2012 - 22:00
Đã gửi 17-04-2012 - 22:00

P/s: đã edit
Bài viết đã được chỉnh sửa nội dung bởi The Gunner: 19-04-2012 - 00:33
- alex_hoang yêu thích
Những ngày cuối cùng còn học toán
winwave1995
#20
 Đã gửi 21-04-2012 - 17:56
Đã gửi 21-04-2012 - 17:56

0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh