Chủ đề này có 5 trả lời

[Crystal]

Balkan MO 2012 - 28 April 2012

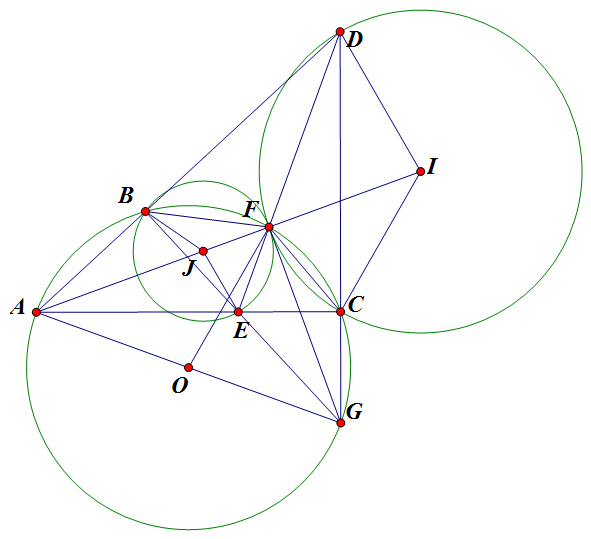
Bài 1. Let $A$, $B$ and $C$ be points lying on a circle $ \Gamma $ with centre $O$. Assume that $ \angle ABC > 90 $. Let $D$ be the point of intersection of the line $AB$ with the line perpendicular to $AC$ at $C$. Let $l$ be the line through $D$ which is perpendicular to $AO$. Let $E$ be the point of intersection of $l$ with the line $AC$, and let $F$ be the point of intersection of $ \Gamma $ with $l$ that lies between $D$ and $E$. Prove that the circumcircles of triangles $ BFE $ and $CFD$ are tangent at $F$.

Bài 2. Prove that \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] for all positive real numbers $x,y$ and $z$.

Bài 3. Let $n$ be a positive integer. Let $ P_{n}=\{2^{n},2^{n-1}\cdot 3, 2^{n-2}\cdot 3^{2},\dots, 3^{n}\}. $ For each subset $X$ of $ P_{n} $, we write $ S_{X} $ for the sum of all elements of $X$, with the convention that $ S_{\emptyset}=0 $ where $ \emptyset $ is the empty set. Suppose that $y$ is a real number with $ 0\leq y\leq 3^{n+1}-2^{n+1}. $

Prove that there is a subset $Y$ of $ P_{n} $ such that $ 0\leq y-S_{Y}< 2^{n} $.

Bài 4. Let $ \mathbb{Z}^{+} $ be the set of positive integers. Find all functions $ f:\mathbb{Z}^{+}\rightarrow\mathbb{Z}^{+} $ such that the following conditions both hold:
(i) $ f(n!)=f(n)! $ for every positive integer $n$,
(ii) $m-n$ divides $ f(m)-f(n) $ whenever $m$ and $n$ are different positive integers.

Bài 1. Cho $A$, $B$ và $C$ là các điểm trên đường tròn $ \Gamma $ tâm $O$. Giả sử $ \angle ABC > 90 $. Gọi $D$ là giao điểm của $AB$ và đường thẳng vuông góc với $AC$ tại $C$. Gọi $l$ là đường thẳng qua $D$ và vuông góc với $AO$. Gọi $E$ là giao điểm của $l$ với $AC$, và $F$ là giao điểm của $ \Gamma $ với $l$ nằm giữa $D$ và $E$. Chứng minh rằng đường tròn ngoại tiếp các tam giác $ BFE $ và $CFD$ tiếp xúc với nhau tại $F$.

Bài 2. Chứng minh rằng \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] với mọi số thực dương $x,y$ và $z$.

Bài 3. Cho $n$ là một số nguyên dương. Đặt $ P_{n}=\{2^{n},2^{n-1}\cdot 3, 2^{n-2}\cdot 3^{2},\dots, 3^{n}\}. $ Với bất kì tập hợp con $X$ của $ P_{n} $, ta kí hiệu $ S_{X}$ là tổng tất cả các phần tử của $X$, với quy ước rằngt $S_{\emptyset}=0$. Giả sử $y$ là một số thực sao cho$ 0\leq y\leq 3^{n+1}-2^{n+1}. $

Chứng minh rằng tồn tại tập hợp con $Y$ của $ P_{n}$ sao cho $ 0\leq y-S_{Y}< 2^{n} $.

Bài 4. Cho$ \mathbb{Z}^{+} $ là tập hợp các số nguyên dương. Tìm tất cả các hàm số $ f:\mathbb{Z}^{+}\rightarrow\mathbb{Z}^{+} $ thỏa mãn đồng thời cả hai điều kiện sau:
(i) $ f(n!)=f(n)! $ với mọi số nguyên dương $n$,
(ii) $m-n$ chia hết $ f(m)-f(n)$, ở đó $m$ và $n$ là hai số nguyên dương khác nhau.

[Tham Lang]

Balkan MO 2012 - 28 April 2012

Bài 2. Prove that \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] for all positive real numbers $x,y$ and $z$.

Áp dụng BDT AM-GM ta có :
$$\sqrt{(x+y)(y+z)(z+x)}\left (\sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}\right )\ge 3\sqrt[6]{\left [(x+y)(y+z)(z+x)\right ]^4}$$
Áp dụng BDT
$$(a+b)(b+c)(c+a)\ge \dfrac{8}{9}(a+b+c)(ab+bc+ca)$$
$$\left (\Leftrightarrow 9((ab(a+b)+bc(b+c)+ca(c+a)+2abc)\ge 8(3abc+ab(a+b)+bc(b+c)+ca(c+a))\Leftrightarrow ab(a+b)+bc(b+c)+ca(c+a)\ge 6abc \right )$$
Đúng theo AM-GM
Áp dụng tiếp BDT
$$a+b+c \ge \sqrt{3(ab+bc+ca)}$$
Ta có :

$$VT \ge 3\sqrt[6]{\left (\dfrac{8}{9}(x+y+z)(xy+yz+zx)\right )^4}\ge 3\sqrt[6]{\dfrac{8^4}{9^4}.\sqrt{3^4(xy+yz+zx)^4}.(xy+yz+zx)^4}=4(xy+yz+zx)$$

[Stranger411]

Balkan MO 2012 - 28 April 2012

Bài 2. Prove that \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] for all positive real numbers $x,y$ and $z$.

Tuy là đề thi quốc gia nhưng mình thấy bài này khá lỏng
Cách 1:
Áp dụng bđt Cauchy-Schwarz, ta có:

$\left( x+y \right)\sqrt{\left( z+x \right)\left( z+y \right)}\ge \left( x+y \right)\left( z+\sqrt{xy} \right)$

$=\left( x+y \right)z+\left( x+y \right)\sqrt{xy}\ge \left( x+y \right)z+2xy$
Cách 2: Bằng cách dùng bổ đề của huymit_95, ta viết lại bđt như sau:
$\sum {\frac{1}{{\sqrt {\left( {x + y} \right)\left( {x + z} \right)} }}} \ge \frac{{4\left( {xy + yz + zx} \right)}}{{\left( {x + y} \right)\left( {y + z} \right)\left( {z + x} \right)}}$
Ta có: $\left( {x + y} \right)\left( {y + z} \right)\left( {z + x} \right) \ge \frac{8}{9}\left( {xy + yz + zx} \right)\left( {x + y + z} \right)$
Nên ta cần chứng minh: $\sum {\frac{1}{{\sqrt {\left( {x + y} \right)\left( {x + z} \right)} }}} \ge \frac{9}{{2\left( {x + y + z} \right)}}$
Và bđt này hoàn toàn đúng với bđt Cauchy-Schwarz:
$\sum {\frac{1}{{\sqrt {\left( {x + y} \right)\left( {x + z} \right)} }}} \ge \sum {\frac{2}{{x + y + 2z}}} \ge \frac{9}{{2\left( {x + y + z} \right)}}$

[perfectstrong]

Bài 1:

Vẽ DC cắt AO tại G. Do $\angle ACG=90^o \Rightarrow$ AG là đường kính của (O) $\Rightarrow$ A,O,G thẳng hàng.
$\Rightarrow \angle ABG=90^o \Rightarrow GB \perp AD$.
Dễ thấy E là trực tâm của $\vartriangle ADG$ nên BG qua E.
Gọi J,I thứ tự là tâm đường tròn ngoại tiếp $\vartriangle BFE,\vartriangle DFC$
\[
\begin{array}{l}
\angle JFE = \frac{{180^o - \angle FJE}}{2} = 90^o - \angle FBE = 90^o - \angle FAG = \angle FGA \\
\angle DFI = \frac{{180^o - \angle FID}}{2} = 90^o - \angle FCD = \angle FCA = \angle FGA \\
\Rightarrow \angle JFE = \angle DFI \Rightarrow \overline {J,F,I} \\
\end{array}
\]
Do đó, suy ra đpcm.

[Ispectorgadget]

Bài 2. Prove that \[ \sum_{cyc}(x+y)\sqrt{(z+x)(z+y)}\geq 4(xy+yz+zx), \] for all positive real numbers $x,y$ and $z$.

Nếu $a=\sqrt{x+y};b=\sqrt{y+z};c=\sqrt{z+x}$ với $a,b,c$ là 3 cạnh 1 tam giác bà $S=\frac{2a^2b^2+2b^2c^2+2a^2c^2-a^4-b^4-c^4}{16}=\frac{xy+xz+yz}{4}$
BĐT Cần chứng minh được viết lại thành
$$abc(a+b+c)\geq 16S\Leftrightarrow \frac{abc}{4S}\geq \frac{4S}{p}\Leftrightarrow R\geq r$$
Đây là 1 kết quả nổi tiếng của Euler

Balkan MO 2012 - 28 April 2012

Bài 4. Let $ \mathbb{Z}^{+} $ be the set of positive integers. Find all functions $ f:\mathbb{Z}^{+}\rightarrow\mathbb{Z}^{+} $ such that the following conditions both hold:
(i) $ f(n!)=f(n)! $ for every positive integer $n$,
(ii) $m-n$ divides $ f(m)-f(n) $ whenever $m$ and $n$ are different positive integers.

TH1: $f(1)=f(2)=1$. Ta có $n!-1|f(n!)-1$ và $n!-2|f(n!)-1$ vậy $f(n!)$ lẻ với mọi n và vì vậy $f(n)=1\forall n\in Z^+$

Mình tìm được lời giải cho bài này do trình tiếng Anh có hạn nên mình dán lời giải ra

Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 21-05-2012 - 16:43

[Ispectorgadget]

Đáp án chính thức của đề này
 bmo2012solutions.pdf   978.16K   140 Số lần tải