Chủ đề này có 452 trả lời

[triethuynhmath]

Bài 127:
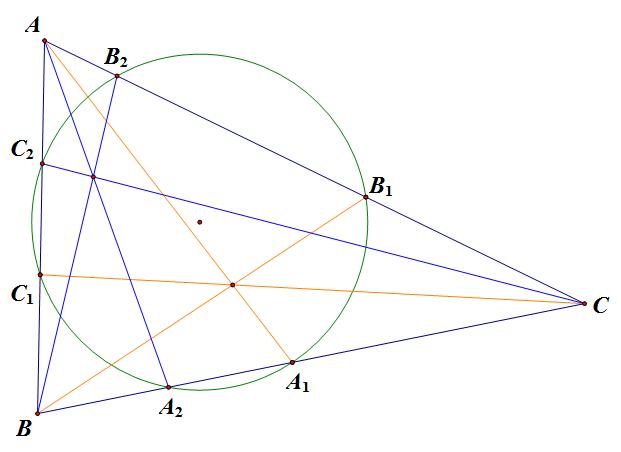
cho ABCDnội tiếp (O). Đường thẳng BD và các tiếp tuyến với (O) tại A và C đồng quy tại S. Gọi I là giao điểm của AC và BD. CMR:
$\frac{SB}{SD}=\frac{IB}{ID}=\frac{AB.CB}{AD.CD}$

Từ điều kiện ta suy ra $ABCD$ là 1 tứ giác điều hòa. Vậy theo tính chất của tứ giác điều hòa ta có: $AB.CD=AD.BC$
Có: $\frac{SB}{SD}=\frac{SB.SD}{SD^2}=\frac{SA^2}{SD^2}=\frac{AB^2}{AD^2}=\frac{AB.BC}{CD.AD}$
Mặt khác ta thấy $(S,I,B,D)=-1$ (Cái này chứng minh = gọi H là giao điểm OS với AC thì $HI,HS$ là phân giác trong, ngoài của tam giác DHB. Vậy $\frac{SB}{SD}=\frac{IB}{ID}(Q.E.D)$

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 05-01-2013 - 20:27

[quangtrinh163]

Ai giúp em bài này với:
Bài 129: Cho (O;$\frac{AB}{2}$). C là một điểm cố định trên (O) thỏa mãn cung AC lớn hơn cung CB. Gọi M là một điểm di động trên cung nhỏ CB (M không trùng B và C). Tia CM cắt đường thẳng AB tại D. Đường tròn ngoại tiếp tam giác OMD cắt đường tròn (O) tại điểm thứ hai là E (E khác M).
a) CM: CE $\perp$ AB
b) CM: E là một điểm cố định khi M di đọng trên cung nhỏ BC
Bài 130: Cho AC là đường chéo lớn của hình bình hành ABCD. Gọi E, F lần lượt là chân dường vuông góc vẽ từ C xuống AB, AD. CM:AB.AE + AD.AF = $AC^{2}$

Bài viết đã được chỉnh sửa nội dung bởi quangtrinh163: 25-12-2012 - 21:52

[henry0905]

Ai giúp em bài này với:
Bài 129:
Bài 130:

Bạn tự vẽ hình nhé!
129)a) $\widehat{MDO}=\widehat{OEM}=\widehat{OME}=\widehat{ODE}$
b) $CE$ vuông góc AB, A,B,C cố định nên E cố định.
130) G,H là hình chiếu của B, D xuống AC thì AB.AE=AG.AC, AD.AF= AH.AC
Mà AH=CG $\Rightarrow$ AG+AH=AC
@: Các bài này mình nghĩ bạn nên post ở topic luyện thi lớp 10 nhé!

[Mefo]

Làm hộ mình bài này với....
Bài 131. Cho tam giác ABC,I là trung diểm BC.Qua I vẽ đường thẳng thứ nhất cắt AB,AC ở M,P;đường thẳng thứ 2 cắt AB,AC ở Q,N.MN,PQ cắt BC ở E,F.Chứng minh IE=IF

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 05-01-2013 - 20:29

[henry0905]

Cho tam giác ABC,I là trung diểm BC.Qua I vẽ đường thẳng thứ nhất cắt AB,AC ở M,P;đường thẳng thứ 2 cắt AB,AC ở Q,N.MN,PQ cắt BC ở E,F.Chứng minh IE=IF

Bài 131: Dùng 4 lần hệ thức Menelaus cho tam giác ABC với các cát tuyến IPM, NIQ, MNE, PFQ, nhân lại ta có IE=IF.
@: Lần sau nhớ đánh dấu bài nha bạn.
______________________________
Beautifulsunrise: Đây chính là định lý con bướm cho cặp đường thẳng.
BT có trong tài liệu sau đây (Nguồn: MathScope.Org):
 ktcs.pdf   3.14MB   122 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 05-01-2013 - 20:46

[HungHuynh2508]

câu 130,từ D vẽ DH vuông vs' AC
$\Delta ADH\sim \Delta ACF (\angle CAF chung;\angle AHD=\angle CFA= 90)$
$\Rightarrow \frac{AD}{AC}=\frac{AH}{AF}\Rightarrow AD.AF=AC.AH$ (1)
$\Delta CDH \sim \Delta ACE(\angle BAC=\angle ACD ; \angle E=\angle CHD=90)$
$\Rightarrow \frac{HC}{AE}=\frac{CD}{AC}\Rightarrow HC.AC=AE.CD$
Mà $CD=AB\Rightarrow AC.HC=AE.AB$ (2)
Từ (1) và (2) $\Rightarrow AE.AB+AD.AH=AC.HC+AH.AC=AC^{2}$

[BlackSelena]

Mình xin phép đổi tên topic thành "Topic hình học THCS"
Bài 132: Cho hình thoi $ABCD$, Tìm quỹ tích điểm $M$ sao cho $MA^2 + MB^2 + MC^2 + MD^2 = 5a^2$ với $a$ là độ dài cạnh hình thoi

[Tru09]

Mình xin phép đổi tên topic thành "Topic hình học THCS"
Bài 132: Cho hình thoi $ABCD$, Tìm quỹ tích điểm $M$ sao cho $MA^2 + MB^2 + MC^2 + MD^2 = 5a^2$ với $a$ là độ dài cạnh hình thoi

Sử dụng công thức đường trung tuyến :
ta có $MA^2 +Mc^2 =2MO^2 +\frac{AC^2}{2}$
$MB^2 +MD^2 =2MO^2 +\frac{BD^2}{2}$
Cộng lại ta có :
$MA^2 +MB^2 +MC^2+ MD^2 =4MO^2 +2a^2$
Mà để $MA^2 +MB^2 +MC^2+ MD^2 =5a^2$
thì $ MO ^2 =\frac{3a^2}{4}$
$\Leftrightarrow MO =\frac{\sqrt{3}a}{2}$
$\Rightarrow$ quỹ tích điểm M là đường tròn tâm $O$ bán kính $\frac{\sqrt{3}a}{2}$
còn giới hạn với mấy cái còn lại để sau nhá

[Tru09]

Góp vui 2 bài :
Hình học cực trị
Bài 133
Cho (O,R) và (O',R') qua O . AB là dây cửa (O) và tiếp xúc với (O') tại C
Tìm Max $(BC^2 +AC^2)$ Theo R và R'
Bài 134
Cho hình vuông ABCD .cạnh a
Vẽ (C,a).E, F $\in$ AB , AD sao cho EF tx (C,a)
TÌm Max $S_{EFC}$ theo $a$

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 05-01-2013 - 20:25

[Beautifulsunrise]

Bài 134
Cho hình vuông ABCD .cạnh a
Vẽ (C,a).E, F $\in$ AB , AD sao cho EF tx (C,a)
TÌm Max $S_{EFC}$ theo $a$

I. Phân tích tìm cách giải:
Khi vẽ hình xong ta thấy ngay để dt tam giác EFC lớn nhất thì EF phải lớn nhất. Vì tam giác EFC có thể suy biến được thành đoạn thẳng AB hoặc AD nên:

II. Lời giải tóm tắt:
Ta có: ${\rm{EF}} \le AE + {\rm{AF}} \Rightarrow 2EF \le AE + {\rm{AF + EF = 2a}} \Rightarrow {\rm{EF}} \le a$
Vậy: $S_{EFC} \le \frac{{{a^2}}}{2}$ Dấu bằng xảy ra khi C trùng B hoặc D.
III. Khai thác và mở rộng bài toán:
BT này đề cập đến cách để 1 tam giác vuông suy biến thành đoạn thẳng. Ngoài yêu cầu tìm Max ta có thể tìm được min của $S_{EFC}$ bằng cách tìm min của EF như sau: Đặt AE = x và AF = y thì ta có:
${\rm{EF = 2a - (x + y) = }}\sqrt {{x^2} + {y^2}} \ge \frac{{x + y}}{{\sqrt 2 }} \Rightarrow x + y \le \frac{{2a\sqrt 2 }}{{\sqrt 2 + 1}} \Rightarrow {\rm{EF}} \ge \frac{{2a}}{{\sqrt 2 + 1}}$
BT sẽ trở nên khó hơn khi người ra đề cố tình ẩn đi đường tròn (C, a) mà chỉ cho E, F lần lượt thuộc AB, AD sao cho $\widehat{ECF} = {45^0}$.

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 05-01-2013 - 20:30

[SupperN]

bài 135:
Cho tam giác ABC, điểm I nằm trong tam giác, tia AI,BI,CI cắt 3 cạnh tại M N P
CMR : $\sqrt{\frac{IA}{IM}} + \sqrt{\frac{IB}{IN}} + \sqrt{\frac{IC}{IP}} \leq \frac{3}{2}$

Bài viết đã được chỉnh sửa nội dung bởi SupperN: 06-01-2013 - 09:34

[Beautifulsunrise]

bài 135:
Cho tam giác ABC, điểm I nằm trong tam giác, tia AI,BI,CI cắt 3 cạnh tại M N P
CMR : $\sqrt{\frac{IA}{IM}} + \sqrt{\frac{IB}{IN}} + \sqrt{\frac{IC}{IP}} \leq \frac{3}{2}$

I. Phân tích:
Dạng bài tập này có cách giải như sau:
Gọi $S_1,~S_2,~S_3$ lần lượt là diện tích của các tam giác IBC, ICA, IAB. Khi đó tính được $\frac{IA}{IM}=\frac{S_2+S_3}{S_1}$; $\frac{IB}{IN}=\frac{S_3+S_1}{S_2}$; $\frac{IC}{IP}=\frac{S_1+S_1}{S_3}$

II: Gợi ý:
Ta có: $\sqrt {\frac{IA}{IM}}+ \sqrt {\frac{IB}{IN}}+\sqrt {\frac{IC}{IP}}$$ \ge \frac{1}{\sqrt{2}}.(\frac{\sqrt{S_2}+\sqrt{S_3}}{S_1}+\frac{\sqrt{S_3}+\sqrt{S_1}}{S_2}+\frac{\sqrt{S_1}+\sqrt{S_2}}{S_3})$$\ge \frac{1}{\sqrt{2}} .6 = 3 .\sqrt{2} > \frac{3}{2} $
III. Khai thác:
Áp dụng công thức ở trên ta còn có:
1)$ \frac{IA}{IM}.\frac{IB}{IN}.\frac{IC}{IP} \ge 8$
2) $ \frac{IM}{IA}+\frac{IN}{IB}+\frac{IP}{IC} \ge \frac{3}{2}$ (BĐT Nesbit cho 3 số)
3) $ \frac{IA}{IM}+\frac{IB}{IN}+\frac{IC}{IP} \ge 6$ (Côsi cho 2 số)

[Beautifulsunrise]

Góp vui 2 bài :
Hình học cực trị
Bài 133
Cho (O,R) và (O',R') qua O . AB là dây cửa (O) và tiếp xúc với (O') tại C
Tìm Max $(BC^2 +AC^2)$ Theo R và R'

I. Phân tích:
Vì điểm C thuộc đoạn thẳng AB nên để đánh giá $CA^2+CB^2$ ta gọi D là trung điểm AB, khi đó $CA^2+CB^2=2(DA^2+DC^2)$. Ở đây cần chú ý là DA, DC đều tính được theo x = OD với R và R' không đổi.

II. Gợi ý:
Ta có: $DA^2+DC^2=R^2-x^2+R'^2-(R'-x)^2=R^2-2x^2+2R'x=R^2+\frac{R'^2}{2}-2(x- \frac{R'}{2})^2 \le R^2+\frac{R'^2}{2}$
Vậy: Max($CA^2+CB^2$ ) $= 2R^2+R'^2$
III. Khai thác:
Giả sử C, B nằm trên cùn nửa mặt phẳng bờ OO', OB cắt (O') tại F, AO cắt (O'), (O) lần lượt tại G, H. Khi đó nhờ KQ bài toán trên ta có thể tìm được Max của BF - GH.

[triethuynhmath]

Đóng góp một bài toán cho topic nào (Dạo này thấy trầm quá ^^):
Bài 136: Cho $\Delta ABC$. Xét 1 đường tròn $(O)$ cắt các cạnh $BC,CA,AB$ lần lượt tại $A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}$.CHứng minh rằng $AA_{1},BB_{1},CC_{1}$ đồng quy $\Leftrightarrow AA_{2},BB_{2},CC_{2}$ đồng quy

[Beautifulsunrise]

Đóng góp một bài toán cho topic nào (Dạo này thấy trầm quá ^^):
Bài 136: Cho $\Delta ABC$. Xét 1 đường tròn $(O)$ cắt các cạnh $BC,CA,AB$ lần lượt tại $A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}$.CHứng minh rằng $AA_{1},BB_{1},CC_{1}$ đồng quy $\Leftrightarrow AA_{2},BB_{2},CC_{2}$ đồng quy

Gợi ý:
Ta có: $AA_1, BB_1, CC_1$ đồng quy $\Leftrightarrow \frac{A_1B}{A_1C}.\frac{B_1C}{B_1A}.\frac{C_1A}{C_1B} = 1 \Leftrightarrow \frac{A_1B}{C_1B}.\frac{B_1C}{A_1C}.\frac{C_1A}{B_1A} =1 \Leftrightarrow \frac{C_2B}{A_2B}.\frac{A_2C}{B_2C}.\frac{B_2A}{C_2A} =1$
$ \Leftrightarrow \frac{C_2B}{C_2A}.\frac{B_2A}{B_2C}.\frac{A_2C}{B_2C}=1 $
$ \Leftrightarrow AA_2, BB_2, CC_2 $đồng quy.

Bài viết đã được chỉnh sửa nội dung bởi Beautifulsunrise: 07-01-2013 - 15:16

[triethuynhmath]

Ứng dụng của đường thẳng Simpson nhé
Bài 137:
Cho tam giác ABC nội tiếp $(O)$. Cho $K,H$ là 2 điểm di động thuộc $(O)$ sao cho $H$ đối xứng $K$ qua $O$. CMR: giao điểm 2 đường thẳng Simpson của $K,H$ đối với $\delta ABC$ thuộc 1 đường cố định

[henry0905]

Ứng dụng của đường thẳng Simpson nhé
Bài 137:
Cho tam giác ABC nội tiếp $(O)$. Cho $K,H$ là 2 điểm di động thuộc $(O)$ sao cho $H$ đối xứng $K$ qua $O$. CMR: giao điểm 2 đường thẳng Simpson của $K,H$ đối với $\delta ABC$ thuộc 1 đường cố định

Gọi các điểm Simson như trong hình vẽ
$90^{0}=\widehat{KCH}=\widehat{HCY}+\widehat{YCK}$
Mà $\widehat{HCY}+\widehat{FHC}=90^{0}$ nên $\widehat{YZK}=\widehat{YCK}$
G, I, J là trung điểm AB, BC, CA.
Ta có XKHD, YKFH, HEKZ là các hình thang
$\Rightarrow$ AY=CF, AX=BD, BE=CZ
GJCI là hình bình hành nên ta cần chứng minh
$\widehat{JTI}=180^{0}-\widehat{ACB}\Leftrightarrow \widehat{JTI}+\widehat{ETI}=90^{0}-\widehat{ACB}$
Từ hai tứ giác EFCH và YKCZ ta có T thuộc đường tròn Euler tam giác ABC.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi henry0905: 08-01-2013 - 21:13

[minhduc3001]

Giả sử hình thang ABCD có diện tích bằng 1 .
Đặt $AC = d_{1} , BD = d_{2}$
Kẻ AM vuông góc CD , BN vuông góc với CD . Đặt Mc = x , ND = y thì x ,y tương ứng là hình chiếu của $d_{1}$ và $d_{2}$ trên CD .
Giả sử $d_{1}\geq d_{2}\Rightarrow x\geq y$
Ta có $2x\geq x+y = MC + ND = DC + MN$
Dễ thấy MN = AB nên $2x\geq x+y=CD+AB$
Trong tam giác vuông AMC , có $AC^{2}=AM^{2}+MC^{2}\geq 2AM. MC \Leftrightarrow d_{1}^{2}=h^{2}+x^{2}\geq 2x.h$ trong đó h = AM là đường cao của hình thang .
Mặt khác $2x.h \geq (CD+AB)h = 2S_{ABCD} \Rightarrow d_{1}^{2}\geq 2\Rightarrow d_{1}\geq \sqrt{2}$
Vậy đườg chéo lớn nhất cua hình thang có độ dài nhỏ nhất là $\sqrt{2}$

Một cách giải hay nhưng khá dài, em có cách làm sau:
Ta có: $S_{ABCD}\leq \frac{1}{2}.d_{1}.d_{2}$ với $d_{1}=AC;d_{2}=BD$. Không mất tính tổng quát ta có thể giả sử $d_{1}\geq d_{2}\Rightarrow S_{ABCD}\leq \frac{1}{2}.d_{1}^{2}\Rightarrow \sqrt{2}\leq d_{1}$
Vậy đường chéo của hình thang có GTNN là $\sqrt{2}$. Dấu bằng xảy ra $\Leftrightarrow d_{_{1}}= d_{_{2}}$ và $d_{1}$ vuông góc với $d_{2}$
Mở rộng 1: Cho tứ giác bất kì có diện tích bằng 1 khi đó đường chéo của tứ giác nhỏ nhất bằng $\sqrt{2}$
Mở rộng 2: Cho tứ giác bất kì có S là a($a> 0$) khi đó đường chéo của tứ giác có GTNN là $\sqrt{a}$

[HungHuynh2508]

Bài 138 Cho $\Delta ABC$ vuông tại A , đường tròn (I) tiếp xúc AB,BC tại P,Q. đường thẳng đi qua trung điểm F của AC và tâm I cắt AB tại E , đường thẳng PQ cắt đường cao AH tại M , đường thẳng vuông góc AC tại F cắt AI ở N , C/m
a, P,Q,N thẳng hàng
b,AE=AM
Bài 139 Cho $\Delta ABC$ cân tại C, đường tròn (O) nội tiếp tam giác tiếp xúc AB,AC,BC tại M,P,N. BO cắt NP tại K. chứng minh ALNM là hình bình hành
Bài 140 Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi $O_{1},O_{2},O_{3},O_{4}$ lần lươt là tâm các đường tròn nội tiếp các tam giác ABC,BCD,CDA,DAB .Chứng minh $O_{1}O_{2}O_{3}O_{4}$ là hình chữ nhật

[BlackSelena]

Bài 140 Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi $O_{1},O_{2},O_{3},O_{4}$ lần lươt là tâm các đường tròn nội tiếp các tam giác ABC,BCD,CDA,DAB .Chứng minh $O_{1}O_{2}O_{3}O_{4}$ là hình chữ nhật

Tham khảo ở đây