
$AB2 + CD2 = AD2 + BC2<=> SABCD = \frac{AC^{2} + BD^{2}}{4}$
Bắt đầu bởi yellow, 12-08-2012 - 08:38
#1
 Đã gửi 12-08-2012 - 08:38
Đã gửi 12-08-2012 - 08:38

Chứng minh tứ giác $ABCD$ có $AB2 + CD2 = AD2 + BC2<=> SABCD = \frac{AC^{2} + BD^{2}}{4}$
$\large{\int_{0}^{\infty }xdx<\heartsuit}$
#2
 Đã gửi 12-08-2012 - 08:58
Đã gửi 12-08-2012 - 08:58

Bài này có nhiều cách giải, mình xin trình bày cách đơn giản nhấtChứng minh tứ giác $ABCD$ có $AB2 + CD2 = AD2 + BC2<=> SABCD = \frac{AC^{2} + BD^{2}}{4}$
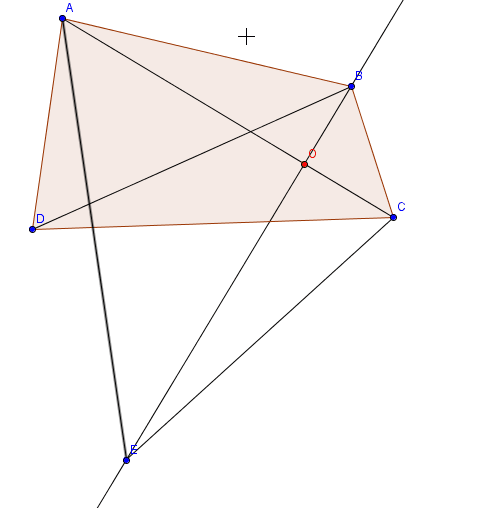
Vẽ BO vuông góc AC tại O
DO phải cắt một trong 2 đoạn thẳng DC,DA. Giả sử BO cắt CD
Trên BO lấy E sao cho CD=CE
Tứ giác ABCE có:
$AB^{2}+CE^{2}=BC^{2}+AE^{2}$
$\Rightarrow AB^{2}+CD^{2}=BC^{2}+AE^{2}$
Mà $\Rightarrow AB^{2}+CD^{2}=BC^{2}+AD^{2}$
$\Rightarrow D\equiv E$
$\Rightarrow$ BD vuông góc AC.
$\Rightarrow S_{ABCD}=\frac{BD.AC}{2}$
Nếu $\frac{BD.AC}{2}=\frac{AC^{2}+BD^{2}}{4}\Leftrightarrow (AC-BD)^{2}=0$
Đẳng thức này chỉ xảy ra khi AC=BD
Mình nghĩ đề bài cho thiếu cái này.
Bài viết đã được chỉnh sửa nội dung bởi henry0905: 12-08-2012 - 09:02
- yellow yêu thích
#3
 Đã gửi 12-08-2012 - 17:03
Đã gửi 12-08-2012 - 17:03

Không đâu bạn ak, Với một tứ giác bất kì mình vẫn chứng minh được đó là dấu $\leq$kẻ AH, BK VUÔNG GÓC với BD
pthagore tam giác ABH=>$AH^2+BH^2=AB^2$
pythgore tam giác CDK:$CD^2=DK^2+CK^2$
=> vt=$AH^2+BH^2+DK^2+CK^2$=$AH^2+DH^2+CK^2+BK^2$
<=>$DK^2+BH^2$=$DH^2+BK^2$
<=>$DH^2+BK^2+2DH*HK+2BK*HK+2HK^2$=$DH^2+BK^2$
<=>$2HK*BD=0$
DĨ NHIÊN BD không thể =O
vậy HK= O
vậy ABCD hình thoi =>s=$\frac{AC.BD}{2}$$\leq$$\frac{AC^2+BD^2}{4}$
có lẻ bạn sai dấu = thành $\leq$
và dấu "=" xảy ra <=>AC=BD khi ABCD hình vuông
(bài mình chỉ vẽ thêm 2 đường cao)
$\large{\int_{0}^{\infty }xdx<\heartsuit}$
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh




