Chủ đề này có 1 trả lời

[l.kuzz.l]

Cho tam giác ABC Ðều cạnh $a$,Ðiểm M tùy ý trong tam giác,O là tâm tam giác,OM=$d$.CMR diện tích tam giác có ba cạnh lần lượt là MA,MB,MC là $\frac{\sqrt{3}}{12}(a^{2}-3d^{2})$

Bài viết đã được chỉnh sửa nội dung bởi l.kuzz.l: 08-09-2012 - 20:54

[perfectstrong]

Thực ra, không cần $M$ nằm trong $\vartriangle ABC$.
Lời giải:
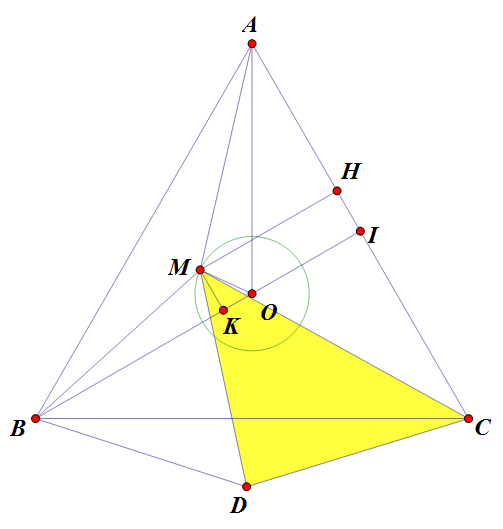
Vẽ $\vartriangle BMD$ sao cho $(\overrightarrow{BD};\overrightarrow{BM}) \equiv (\overrightarrow{BC};\overrightarrow{BA}) \equiv \dfrac{\pi}{3} \pmod{2\pi}$.
Khi đó, dễ thấy $\vartriangle BCD=\vartriangle BAM$ nên $MA=CD$.
Ta chỉ cần tính $S_{MCD}$
Do tính đối xứng của $\vartriangle ABC$ nên ta chỉ cần xét TH $M$ nằm trong góc $AOB$ và $\angle BOM \le 60^o$.
Hạ $OI \perp AC; MH \perp AC; MK \perp BOI$. Đặt $MH=h$.Dễ thấy $OI=\dfrac{a}{\sqrt{3}}$

\[
\begin{array}{l}
S_{MDC} = S_{MBC} + S_{DBC} - S_{BMD} = S_{MBC} + S_{MBA} - S_{MBD} \\
= S_{ABC} - S_{MAC} - S_{BMD} = \frac{{a^2 \sqrt 3 }}{4} - \frac{{ah}}{2} - \frac{{MB^2 \sqrt 3 }}{4} \\
MB^2 = OM^2 + OB^2 - 2OM.OB\cos BOM \\
= d^2 + \frac{{a^2 }}{3} - \frac{{2ad}}{{\sqrt 3 }}\cos BOM \\
\left. \begin{array}{l}
MH = KI = h \\
OK = KI - OI = h - \frac{a}{{2\sqrt 3 }} \\
\end{array} \right\} \Rightarrow \cos BOM = \frac{{OK}}{{OM}} = \frac{{2\sqrt 3 h - a}}{{2\sqrt 3 d}} \\
\Rightarrow MB^2 = d^2 + a^2 - \frac{{2ad}}{{\sqrt 3 }}.\frac{{2\sqrt 3 h - a}}{{2\sqrt 3 d}} = d^2 + \frac{{2a^2 }}{3} - \frac{{2\sqrt 3 ah}}{3} \\
\Rightarrow S_{MDC} = \frac{{a^2 \sqrt 3 }}{4} - \frac{{ah}}{2} - \frac{{\sqrt 3 }}{4}\left( {d^2 + \frac{{2a^2 }}{3} - \frac{{2\sqrt 3 ah}}{3}} \right) = \frac{{\sqrt 3 }}{4}\left( {a^2 - 3d^2 } \right) \\
\end{array}
\]