Chủ đề này có 7 trả lời

[soros_fighter]

Các bạn download link dưới nhé

File gửi kèm

•  de chon doi tuyen ha tinh vong 1_2012-2013.doc   43K   324 Số lần tải
•  de chon doi tuyen ha tinh vong 2-2012-2013.doc   42.5K   269 Số lần tải

[T M]

$$\begin{array}{|c|c|c|c|c|c|}
\hline
\textbf{SỞ GIÁO DỤC VÀ ĐÀO TẠO} & \textbf{KỲ THI CHỌN ĐỘI TUYỂN DỰ THI } \\
\hline
\textbf{HÀ TĨNH} & \textbf{HỌC SINH GIỎI QUỐC GIA LỚP 12 THPT} \\
\hline
\textbf{ĐỀ CHÍNH THỨC} & \textbf{NĂM HỌC 2012-2013} \\
\hline
\textbf{(Đề thi có 01 trang, gồm 5 câu)} & \textbf{Môn: TOÁN - Vòng 1} \\
\hline
\textbf{} & \textbf{Thời gian làm bài: 180 phút} \\
\hline
\end{array}$$

Câu 1. Giải hệ phương trình:

\[\left\{ \begin{align} & {{\left( \frac{1-{{x}^{2}}}{{{x}^{2}}} \right)}^{3}}+xy+\frac{3}{2}={{y}^{3}} \\& {{(xy+2)}^{2}}+\frac{1}{{{x}^{2}}}=2y+\frac{4}{x} \\\end{align} \right.\]

Câu 2. Dãy số (a_n) được xác định:

$$\left\{\begin{matrix} a_1=1, a_2=2\\ a_{n+2}=2a_{n+1}-a_{n}+2\,\,\,\,\ , \forall n\in \mathbb{N}^* \end{matrix}\right.$$

Xét xem số $u_k=a_{k+2012}.a_{k+2013}$ với $k \in \mathbb{N}^*$ có phải là số hạng của dãy số $(a_n)$ hay không?

Câu 3. Chứng minh rằng phương trình sau có vô số nghiệm nguyên

\[2011{{x}^{2}}-2012{{y}^{2}}+{{2013}^{2}}=0\]

Câu 4. Cho tam giác nhọn $ABC$ nội tiếp đường tròn $(O)$ có $H$ là trực tâm. Gọi $A', B', C'$ theo thứ tự là giao điểm thứ hai của các đường thẳng $AH, BH, CH$ với đường tròn $(O)$. Một điểm $D$ nằm trên đường tròn ($D$ khác các điểm $A, B, C, A’, B’, C’$). Gọi $A'', B'', C''$ là giao điểm lần lượt của $DA'$ với $BC, DB'$ với $AC, DC'$ với $AB$. Chứng minh rằng bốn điểm $A'', B'', C''$ và $H$ thẳng hàng.

Câu 5. Trong kỳ thi chọn đội tuyển học sinh giỏi toán của một tỉnh có 20 em tham gia. Mỗi học sinh phải thi 2 vòng, mỗi vòng được gọi là một bài thi. Điểm của mỗi bài thi được cho là một số tự nhiên từ 1 đến 10. Phương thức chọn đội tuyển là so sánh kết quả điểm của từng bài thi tương ứng (vòng 1, vòng 2 ) giữa các thí sinh. Thí sinh A gọi là so sánh được với thí sinh B nếu điểm mỗi bài thi của A không nhỏ hơn điểm mỗi bài thi tương ứng của B. Biết rằng không có hai thí sinh nào có cùng cặp điểm số tương ứng. Chứng minh rằng có thể chọn được ba thí sinh A, B, C sao cho A so sánh được với B và B so sánh được với C.

_____________ HẾT _____________

- Thí sinh không được sử dụng tài liệu.

- Giám thị không giải thích gì thêm.

Họ và tên thí sinh:.................................. Số báo danh:....................

Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 30-09-2012 - 12:22

[E. Galois]

Câu 1. Chứng minh rằng $\forall m \in \mathbb{R}$, phương trình sau luôn có nghiệm thực:
$$m^3sin^4x – 2m^3sin^2x + sinx + m^3 – m = 0$$.

Câu 2. Cho ba số thực dương $a, b, c$ thỏa mãn: $ab + bc + ca = 3abc$. Tìm giá trị nhỏ nhất của biểu thức:
\[P = \left( {\frac{a}{b} - \frac{1}{b} + \frac{1}{{ab}}} \right)\left( {\frac{b}{c} - \frac{1}{c} + \frac{1}{{bc}}} \right)\left( {\frac{c}{a} - \frac{1}{a} + \frac{1}{{ca}}} \right)\].

Câu 3. Chứng minh rằng với mọi số nguyên dương $n$ thì
\[{S_n} = C_{2n + 1}^0{.2^{2n}} + C_{2n + 1}^2{.2^{2n - 2}}.3 + C_{2n + 1}^4{.2^{2n - 4}}{.3^2} + ... + C_{2n + 1}^{2n}{.3^n}\]
là tổng của hai số chính phương liên tiếp.

Câu 4. Cho 3 điểm $A, B, C$ phân biệt và thẳng hàng (theo thứ tự đó). Gọi $d$ và $\Delta$ lần lượt là các đường thẳng vuông góc với đường thẳng $AC$ tại $A$ và $C$; $M$ là một điểm di động trên $\Delta$ . Từ $M$ kẻ các tiếp tuyến $MD, ME$ đến đường tròn đường kính $AB$ với $D, E$ là các tiếp điểm. Các tiếp tuyến đó cắt $d$ tương ứng tại các điểm $P, Q$. Gọi $R$ và $S$ lần lượt là giao điểm của $d$ với các đường thẳng $BD$ và $BE$.
a) Chứng minh rằng đường tròn ngoại tiếp tam giác $BRS$ luôn đi qua hai điểm cố định.
b) Xác định vị trí của điểm $M$ trên $\Delta$ để tam giác $MPQ$ có chu vi nhỏ nhất.

Câu 5 . Cho đa thức $f(x)$ với hệ số thực, có bậc không nhỏ hơn 1 và đồng thời thoả mãn hai điều kiện sau:
a. Phương trình $f(x) = 0$ không có nghiệm bội.
b. $f(x).f(y) \le {\left[ {f\left( {\frac{{x + y}}{2}} \right)} \right]^2},\forall x,y \in \mathbb{R}$.
Chứng minh rằng phương trình $f(x) = 0$ có duy nhất một nghiệm thực.

[perfectstrong]

Nhắm nổi mỗi bài này
Ngày 1:
Bài 4:

\[
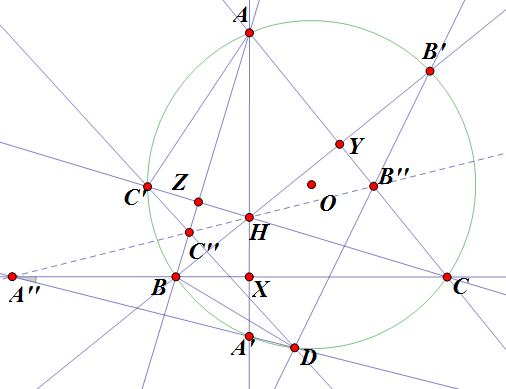
\begin{array}{rcl}
\left( {C''H;BC} \right) &\equiv & \left( {C''H;AB} \right) + \left( {AB;BC} \right)\left( {\bmod \pi } \right) \\
&\equiv &\left( {AB;DC'} \right) + \left( {AB;BC} \right)\left( {\bmod \pi } \right) \\
&\equiv &\left( {C'D;C'A} \right) + \left( {C'A;AB} \right) + \left( {AB;AC} \right)\left( {\bmod \pi } \right) \\
&\equiv &\left( {BD;BA} \right) - \left( {AH;AB} \right) + \left( {AB;AC} \right)\left( {\bmod \pi } \right) \\
&\equiv &\left( {BD;BC} \right) + \left( {AB;AH} \right)\left( {\bmod \pi } \right) \\
&\equiv &\left( {BD;BC} \right) + \left( {DB;DA'} \right)\left( {\bmod \pi } \right) \\
&\equiv &- \left( {A''D;BC} \right) \equiv \left( {A''H;BC} \right)\left( {\bmod \pi } \right) \\
\end{array}
\]
Suy ra $A'';C'';H$ thẳng hàng. Tương tự, $B'';A'';H$ thẳng hàng nên ta có đpcm.
=======================
Điểm $D$ trong bài này là điểm Anti-Steiner thì phải

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 30-09-2012 - 21:05

[WhjteShadow]

Sau khi đổi biến $ab+bc+ca=q\leq 3,abc=r\leq 1$ thì ta có:
$$P=r^2-qr+q^2-4q+7-r$$
Ta sẽ chứng minh $P\geq 1$ hay là:
$$r^2-qr+q^2-4q+6-r\geq 0$$
$$\Leftrightarrow r^2+q^2+6\geq qr+4q+r$$
Nhưng điều này đúng khi ta cộng 4 bất đẳng thức hiển nhiên the0 $AM-GM$:
$$\frac{2}{3}q^2+6\geq 4q\,\, , \,\,r^2+\frac{1}{9}q^2\geq \frac{2}{3}qr $$
$$\frac{1}{9}q^2\geq \frac{1}{3}qr\,\, , \,\,\frac{1}{9}q^2\geq r$$
Vậy $Min_P=1$.Dấu bằng xảy ra tại $a=b=c=1$
Trong khi làm bài này em có 1 phát hiện thú vị sau:
$$\left( {\frac{a}{b} - \frac{1}{b} + \frac{1}{{ab}}} \right)\left( {\frac{b}{c} - \frac{1}{c} + \frac{1}{{bc}}} \right)\left( {\frac{c}{a} - \frac{1}{a} + \frac{1}{{ca}}} \right)=(a^2-a+1)(b^2-b+1)(c^2-c+1)$$

[thanh hai nguyen]

theo mình có thể giải bằng đạo hàm (chưa chắc đúng )
đặt 1/a=x,1/b=y,1/c=z => x+y+z = 3.khi đó:
P= (x² - x +1)(y²-y+1)(z²-z+1).
mà x²+1 >=(1/2)(x+1)².tương tự cho y,zsuy ra:
P>= (1/8)(x²+1)(1+y²)(z²+1) >=(1/8)(x+y)²(z²+1) =(1/8)(3-z)²(z²+1)=f(Z).
nếu giả sử x>=y>=z thì 0<z<=1.từ đó khảo sát hàm số.
sorry nha. không biết gõ công thức toán nên bài làm xấu. Mà có sai cũng đừng chửi nha!!!!!!!!. mình ngu toán lắm

[thanh hai nguyen]

câu 1(hệ phương trình)
từ phương trình thứ 2 suy ra: xy+2=1/x => y=1/x²-2/x.
đặt a=1/x,thế vào phương trình thứ nhất sẽ giải ra (chú ý có nhân tử chung 2a-1)

[bongsuababy]

a) Chứng minh quy nạp $a_{n}$ có dạng:
$a_{n}= \left ( n-1 \right )^{2} +1$ (1)
- Với n=1 thì $a_{1}$=1(t/m)
- Giả sử n=k thì $a_{k}= \left ( k-1 \right )^{2} +1$
- Chứng minh với n=k+1 thì:
$a_{k+1}= k^{2} +1$
Thật vậy, ta có:
$a_{k+1}= 2a_{k} - a_{k-1} +2$
Theo tính chất truy hồi thì:
$a_{k-1}= \left ( k-2 \right )^{2}+1$
=> $a_{k+1}=2\left ( k-1 \right )^{2} +2- \left ( k-2 \right )^{2} -1+2$
=> $a_{k+1}= k^{2} +1$
Vậy $a_{n}= \left ( n-1 \right )^{2} +1$
b) Ta có:
$a_{k+2012} = \left ( k+2011 \right )^{2}$
$a_{k+2013} = \left ( k+2012 \right )^{2}$
=> $u_{k}= a_{k+2012}.a_{k+2013} = \left [ \left ( k+1 \right )^{2} +1\right ].\left [ \left ( k+2012 \right )^{2}+1 \right ]$
= $\left [ \left ( k+2011 \right ).\left ( k+2012 \right ) +1 \right ]^{2} +1$
=> $u_{k}$ có dạng $\left ( t-1 \right )^{2} +1$
=> $u_{k}$ cũng là số hạng dãy $a_{n}$

Bài viết đã được chỉnh sửa nội dung bởi bongsuababy: 07-10-2012 - 22:11