Giải:
Giả sử 2 nghiệm của phương trình là ${x_1},{x_2}$. Theo Viete, ta có: $\left\{ \begin{array}{l}
{x_1} + {x_2} = - \dfrac{b}{a}\\
{x_1}{x_2} = \dfrac{c}{a}
\end{array} \right.$
Khi đó: $$P = \dfrac{{\dfrac{{\left( {a - b} \right)\left( {2a - b} \right)}}{{{a^2}}}}}{{\dfrac{{a - b + c}}{a}}} = \dfrac{{\left( {1 - \dfrac{b}{a}} \right)\left( {2 - \dfrac{b}{a}} \right)}}{{1 - \dfrac{b}{a} + \dfrac{c}{a}}} = \dfrac{{\left( {1 + {x_1} + {x_2}} \right)\left( {2 + {x_1} + {x_2}} \right)}}{{1 + {x_1} + {x_2} + {x_1}{x_2}}}$$
$$ = \dfrac{{2\left( {1 + {x_1} + {x_2} + {x_1}{x_2}} \right) + {x_1} + {x_2} + x_1^2 + x_2^2}}{{1 + {x_1} + {x_2} + {x_1}{x_2}}} = 2 + \dfrac{{{x_1} + {x_2} + x_1^2 + x_2^2}}{{1 + {x_1} + {x_2} + {x_1}{x_2}}}$$
Không mất tính tổng quát, giả sử $0 \le {x_1} \le {x_2} \le 1$ $ \Rightarrow x_1^2 \le {x_1}{x_2} \Rightarrow 1 + {x_1} + {x_2} + {x_1}{x_2} \ge 1 + x_1^2 + {x_1} + {x_2}$
$$ \Rightarrow \dfrac{{{x_1} + {x_2} + x_1^2 + x_2^2}}{{1 + {x_1} + {x_2} + {x_1}{x_2}}} \le \dfrac{{{x_1} + {x_2} + x_1^2 + x_2^2}}{{1 + x_1^2 + {x_1} + {x_2}}} \le \dfrac{{{x_1} + {x_2} + x_1^2 + x_2^2}}{{x_1^2 + x_2^2 + {x_1} + {x_2}}} = 1$$
$ \Rightarrow P \le 2 + 1 = 3$. Dấu "=' xảy ra $ \Leftrightarrow {x_1} = {x_2} = 1$
Vậy $\max P = 3 \Leftrightarrow {x_1} = {x_2} = 1$.
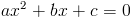 có 2 nghiệm thuộc [0;1].tìm giá trị lớn nhất của biểu thức
có 2 nghiệm thuộc [0;1].tìm giá trị lớn nhất của biểu thức

