Đề bài:
Cho hình tứ diện $ABCD$,gọi $A_{1};B_{1},C_{1};D_{1}$ lần lượt là trọng tâm các mặt đối diện với các đỉnh $A,B,C,D$.Các đường thẳng $AA_{1},BB_{1},CC_{1},DD_{1}$ cắt mặt cầu tứ diện $ABCD$ theo thứ tự tại $A_{2},B_{2},C_{2},D_{2}$.
Chứng minh rằng:
$\frac{AA_{1}}{AA_{2}} =\frac{BB_{1}}{BB_{2}}+\frac{CC_{1}}{CC_{2}}+\frac{DD_{1}}{DD_{2}} \leq \frac{8}{3}$
Toán thủ ra đề nguyenhang28091996
__________________________
- Thời gian bắt đầu tính từ 21:00 ngày 16/11/2012
- Toán thủ ra đề không phải làm bài
bài này hình như đề bị sai!theo như đính chính lại đề của
nguyenhang28091996 thì đề như sau:
Đề bài:
Cho hình tứ diện $ABCD$,gọi $A_{1};B_{1},C_{1};D_{1}$ lần lượt là trọng tâm các mặt đối diện với các đỉnh $A,B,C,D$.Các đường thẳng $AA_{1},BB_{1},CC_{1},DD_{1}$ cắt mặt cầu tứ diện $ABCD$ theo thứ tự tại $A_{2},B_{2},C_{2},D_{2}$.
Chứng minh rằng:
$\frac{AA_{1}}{AA_{2}} +\frac{BB_{1}}{BB_{2}}+\frac{CC_{1}}{CC_{2}}+\frac{DD_{1}}{DD_{2}} \leq \frac{8}{3}$
do vậy, bài giải của em như sau:
trước tiên, ta tìm công thức tính $AA_1^{2}$
gọi $H$ là trung điểm $BA_1$
ta có: $AA_1^{2}=\frac{2AH^{2}+2AK^{2}-HK^{2}}{4}$
$\quad K$ là điểm nào?$\Rightarrow 4AA_1^{2}=2AH^{2}+2AK^{2}-HK^{2}$
Định lý gì đây?$\Rightarrow 4AA_1^{2}=2\frac{2AB^{2}+2AA_1^{2}-BA_1^{2}}{4}+2.\frac{2b^{2}+2c^{2}-y^2}{4}-HK^{2}$
$\Rightarrow 8AA_1^{2}=2a^{2}+2AA_1^{2}-BA_1^{2}+2b^{2}+2c^{2}-y^{2}-2HK^{2}$
do $BA_1=HK=\frac{2}{3}BK$,
nên: $6AA_1^{2}=2a^{2}+2b^{2}+2c^{2}-y^{2}-3\frac{4}{9}BK^{2}$
$\Rightarrow 6AA_1^{2}=2a^{2}+2b^{2}+2c^{2}-y^{2}-\frac{1}{3}(2x^{2}+2z^{2}-y^{2}) $
$\Rightarrow 18AA_1^{2}=6a^{2}+6b^{2}+6c^{2}-2x^{2}-2y^{2}-2z^{2} $
$\Rightarrow 9AA_1^{2}=3a^{2}+3b^{2}+3c^{2}-x^{2}-y^{2}-x^{2}$
$\Rightarrow AA_1^{2}=\frac{1}{3}(a^{2}+b^{2}+c^{2})-\frac{1}{9}(x^{2}+y^{2}+z^{2})$
trở lại bài toán!
ta có:$AA_1.AA_2=BA_1.A_1B'$
$= \frac{2}{3}BM.(A_1M+MB') $
$= \frac{2}{3}BM(\frac{1}{3}BM+MB') $
$=\frac{2}{9}BM^{2}+\frac{2}{3}BM.MB' $
$= \frac{2}{9}BM^{2}+\frac{2}{3}MC.MD $
$= \frac{2}{9}(\frac{x^{2}+z^2}{2}-\frac{y^{2}}{4})+\frac{2}{3}.\frac{1}{4}y^{2} $
$= \frac{1}{9}(x^{2}+y^{2}+z^{2})$
suy ra:$\frac{AA_1}{AA_2}$
$=1-\frac{AA_1.AA_2}{AA_1^{2}+AA_1.AA_2} $
$= 1-\frac{1}{3}(\frac{x^{2}+y^{2}+z^{2}}{a^{2}+b^{2}+c^{2}})$
tương tự:
$\frac{BB_1}{BB_2}= 1-\frac{1}{3}(\frac{b^{2}+c^{2}+y^{2}}{a^{2}+z^{2}+x^{2}}) $
$\frac{CC_1}{CC_2}= 1-\frac{1}{3}(\frac{a^{2}+c^{2}+z^{2}}{x^{2}+b^{2}+y^{2}}) $
$\frac{DD_1}{DD_2}= 1-\frac{1}{3}(\frac{a^{2}+b^{2}+x^{2}}{z^{2}+c^{2}+y^{2}})$
do đó:
$S=\frac{AA_1}{AA_2}+\frac{BB_1}{BB_2}+\frac{CC_1}{CC_2}+\frac{DD_1}{DD_2}=4-\frac{1}{3}(\frac{x^{2}+y^{2}+z^{2}}{a^{2}+b^{2}+c^{2}}+\frac{b^{2}+c^{2}+y^{2}}{a^{2}+z^{2}+x^{2}}+\frac{a^{2}+c^{2}+z^{2}}{x^{2}+b^{2}+y^{2}}+\frac{a^{2}+b^{2}+x^{2}}{z^{2}+c^{2}+y^{2}})$
ta thấy:$((a^{2}+b^{2}+c^{2})+(a^{2}+z^{2}+x^{2})+(x^{2}+b^{2}+y^{2})+(z^{2}+c^{2}+y^{2}))\geq 4\sqrt[4]{(a^{2}+b^{2}+c^{2}).(a^{2}+z^{2}+x^{2}).(x^{2}+b^{2}+y^{2}).(z^{2}+c^{2}+y^{2})}$
và: $\frac{1}{a^{2}+b^{2}+c^{2}}+\frac{1}{a^{2}+z^{2}+x^{2}}+\frac{1}{x^{2}+b^{2}+y^{2}}+\frac{1}{z^{2}+c^{2}+y^{2}}\geq 4\frac{1}{\sqrt[4]{(a^{2}+b^{2}+c^{2}).(a^{2}+z^{2}+x^{2}).(x^{2}+b^{2}+y^{2}).(z^{2}+c^{2}+y^{2})}}$
suy ra:$((a^{2}+b^{2}+c^{2})+(a^{2}+z^{2}+x^{2})+(x^{2}+b^{2}+y^{2})+(z^{2}+c^{2}+y^{2})).(\frac{1}{a^{2}+b^{2}+c^{2}}+\frac{1}{a^{2}+z^{2}+x^{2}}+\frac{1}{x^{2}+b^{2}+y^{2}}+\frac{1}{z^{2}+c^{2}+y^{2}})\geq 16$
$\Leftrightarrow \frac{x^{2}+y^{2}+z^{2}}{a^{2}+b^{2}+c^{2}}+\frac{b^{2}+c^{2}+y^{2}}{a^{2}+z^{2}+x^{2}}+\frac{a^{2}+c^{2}+z^{2}}{x^{2}+b^{2}+y^{2}}+\frac{a^{2}+b^{2}+x^{2}}{z^{2}+c^{2}+y^{2}}\geq 4$
Vậy $S\leq 4-\frac{1}{3}.4= \frac{8}{3}$
đẳng thức xảy ra khi và chỉ khi:$a=b=c=x=y=z$$\Leftrightarrow$ tứ diện $ABCD$ là tứ diện đều!
 hinh.bmp 634.55K
266 Số lần tải
hinh.bmp 634.55K
266 Số lần tải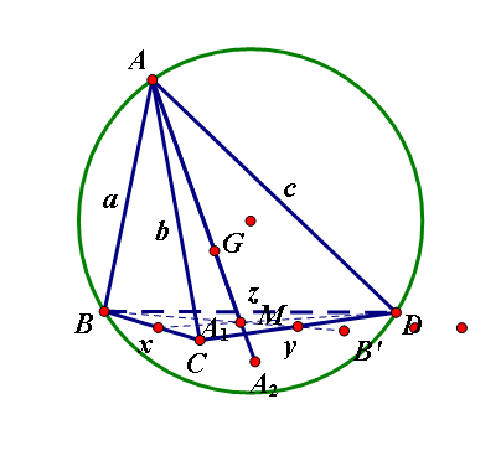
________________________________
Bài làm: $d=1$$S=\left\lfloor\dfrac{52-0}{2}\right\rfloor+3\times 1+0+0=29$
Bài viết đã được chỉnh sửa nội dung bởi hxthanh: 29-11-2012 - 21:21
Chấm điểm!

 Chủ đề bị khóa
Chủ đề bị khóa












