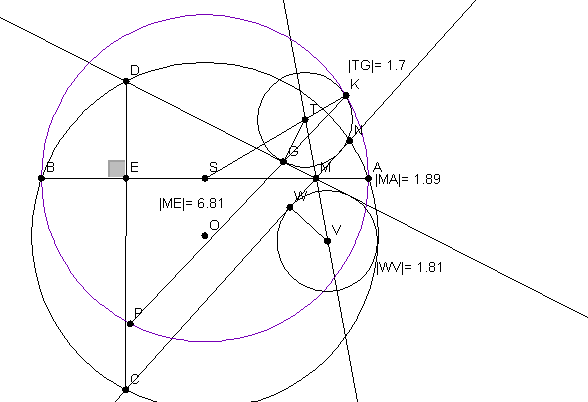
Chứng minh rằng: $\frac{1}{r}= \frac{1}{MA}+\frac{1}{ME}$
#1
 Đã gửi 28-12-2012 - 16:18
Đã gửi 28-12-2012 - 16:18

Bài 2: Cho tam giác ABC không cân tại A, M là trung điểm của BC. Điểm I thoả mãn điều kiện IB = IC. Đường tròn (I, IA) theo thứ tự lại cắt AB, AC tại P, Q. PQ cắt BC tại K. AM lại cắt (I, IA) tại L. Chứng minh rằng KL tiếp xúc với (I, IA).
- cool hunter và Sagittarius912 thích
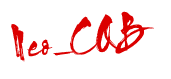
#2
 Đã gửi 29-12-2012 - 10:47
Đã gửi 29-12-2012 - 10:47

Bài 2: Cho tam giác ABC không cân tại A, M là trung điểm của BC. Điểm I thoả mãn điều kiện IB = IC. Đường tròn (I, IA) theo thứ tự lại cắt AB, AC tại P, Q. PQ cắt BC tại K. AM lại cắt (I, IA) tại L. Chứng minh rằng KL tiếp xúc với (I, IA).

$P_{B/(I)}=P_{C/(I)}\Rightarrow BE.BA=CQ.CA$
mà $\frac{KP}{KQ}.\frac{CQ}{CA}.\frac{BA}{BP}=1$
nên $\frac{KP}{KQ}=\left ( \frac{AC}{AB} \right )^2$
mặt khác $\frac{PL}{LQ}=\frac{sinMAB}{sinMAC}=\frac{AM.\frac{sinAMB}{AB}}{AM.\frac{sinAMC}{AC}}=\frac{AC}{AB}$
do đó $\frac{KP}{KQ}=\left ( \frac{PL}{LQ} \right )^2$
từ K kẻ tiếp tuyến $KL'$ của $(I)$ ( $L'$ thuộc cung $PQ$ chứa L )
thì $\frac{KP}{KQ}=\left ( \frac{PL'}{L'Q} \right )^2$
do đó $L \equiv L'$ hay ta có đpcm
- perfectstrong, cool hunter, tran thanh binh dv class và 2 người khác yêu thích
Thế giới này là một sai lầm của tạo hóa…
Cảm xúc là một sai lầm của con người…
Niềm tin cũng là một sai lầm…là cách tự xác ngu xuẩn nhất…
#3
 Đã gửi 29-12-2012 - 15:49
Đã gửi 29-12-2012 - 15:49

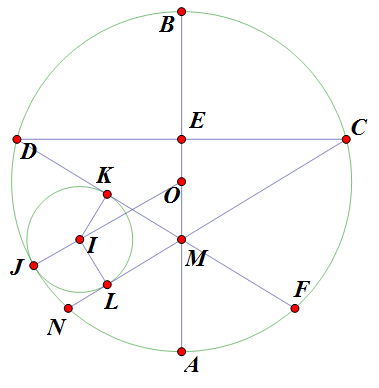
Gọi $F$ là giao điểm thứ hai của đường tròn ngoại tiếp $ABC$ và đường tròn tâm $I$. Vì $I$ nằm trên trung trực của $BC$ nên dễ thấy $AF\parallel BC$ và hai điểm $A, F$ đối xứng với nhau qua $IM$.
$\angle PKB = \angle ACB - \angle AQP = \angle AFB - \angle AFP = \angle PFB$, tứ giác $PFKB$ nội tiếp. Do đó $\angle FKC = \angle APF = \angle AQF$, tứ giác $FKCQ$ cũng nội tiếp dẫn đến $\angle KFQ = \angle ACB = \angle CAF$, điều này có nghĩa là $KF$ là tiếp tuyến từ $K$ tới đường tròn tâm $I$.
Tiếp thấy $\angle ALF = \angle AQF = \angle MKF$, tứ giác $FKLM$ nội tiếp nên $\angle FLK = \angle FMK = \angle AMB = \angle MAF = \angle LFK$, tam giác $KLF$ là tam giác cân, $KL = KF$ dẫn đến $KL$ là tiếp tuyến thứ hai từ $K$ tới đường tròn tâm $I$.
Bài viết đã được chỉnh sửa nội dung bởi khongcanten: 29-12-2012 - 15:59
- perfectstrong, tran thanh binh dv class và baoquoc thích
#4
 Đã gửi 29-12-2012 - 15:57
Đã gửi 29-12-2012 - 15:57

- tran thanh binh dv class yêu thích
#5
 Đã gửi 29-12-2012 - 21:17
Đã gửi 29-12-2012 - 21:17

Bạn vẽ hình sai thì phải? Đề cho $AB$ là đường kính đường tròn ban đầu luôn cơ mà? Có cách vẽ chính xác đường tròn $(I)$ luôn.tran thanh binh dv class thử xem lại đề bài bài 1 xem sao. Vì $D$ có thể có hai vị trí không tương đương nên $r$ có thể có hai giá trị cũng không tương đương. Vì thế cần phải xác định chính xác hơn vị trí của $D$. Tuy vậy, theo như bài ra thì cả hai giá trị có thể của $r$ xem ra đều không thỏa mãn đẳng thức $1/r = 1/MA + 1/ME$.
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 29-12-2012 - 21:19
- tran thanh binh dv class yêu thích
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh