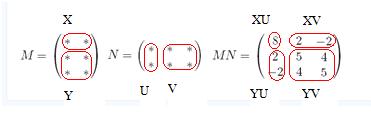$MN=\begin{bmatrix} 8 & 2 & -2\\ 2 & 5 & 4\\ -2 & 4 & 5 \end{bmatrix}$ Tìm NM?
#1
 Đã gửi 10-01-2013 - 02:14
Đã gửi 10-01-2013 - 02:14

Tìm NM?
- cuong148 và YeuEm Zayta thích
#2
 Đã gửi 01-02-2013 - 08:39
Đã gửi 01-02-2013 - 08:39

Anh Đức post lời giải lên được không ạ.Cho M là ma trận cấp 3x2 và N là ma trận cấp 2x3 thỏa $MN=\begin{bmatrix} 8 & 2 & -2\\ 2 & 5 & 4\\ -2 & 4 & 5 \end{bmatrix}$
Tìm NM?
Em chỉ thấy mỗi Trace và det là không đổi.Nhưng thế thì vẫn thiếu dữ kiện.
Không biết từ cái đối xứng của MN thu thêm đưọc cái gì không.@@.Mong anh gợi ý.em nghĩ mấy ngày rồi.
#3
 Đã gửi 01-02-2013 - 09:50
Đã gửi 01-02-2013 - 09:50

Bài này là đề Olympic của nước ngoài hình như là lâu lắm rồi. Nhưng năm 2009 thì ĐH Quy Nhơn lấy nó làm đề dự tuyển năm đó.
Dưới đây là lời giải của mình. hi.
....................
Ta dể dàng tính được rằng
$(MN)^{2}=9(MN)$
$rank(MN)=2$
Ta có:
$2=rank(MN)=rank(\frac{1}{9}(MN)^{2})=rank(MNMN \leq rank(NM)$
Mà $NM \in M_{2}(\mathbb{K})$ nên $rank(NM)=2$
Suy ra $NM$ khả nghịch.
Ta có:
$(NM)^{2}=NMNM=N.\frac{1}{9}(MN)^{2}.M=\frac{1}{9}(NM)^{3}$
Suy ra $NM=9I_{2}$ vì $NM$khả nghịch
.......................
Trong quá trình chứng minh có sử dụng kết quả sau:
"$\forall (A, B, C) \in M_{n,p}(\mathbb{K}) \times M_{p,q}(\mathbb{K}) \times M_{q,r}(\mathbb{K}), rank(ABC) \leq rank(B)$"
Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 17-03-2014 - 07:16
- cuong148 yêu thích
#4
 Đã gửi 01-02-2013 - 10:01
Đã gửi 01-02-2013 - 10:01

Vì $det(MN)=det(NM)=0$.nhưng theo bài anh thì $det(NM)=81$
Có chỗ không ổn ở $(MN)^2$ vì rank của nó phải là 1.
Anh nghĩ ra được cái $(MN)^2=9MN$ thật tuyệt.@@.
Liệu rằng khi người ta cho $A^n=mA$ thì có tính được A???
À còn 1 điều lạ lùng nữa.9 lại chính là giá trị riêng của A.
Bài viết đã được chỉnh sửa nội dung bởi cuong148: 01-02-2013 - 10:11
#5
 Đã gửi 01-02-2013 - 10:10
Đã gửi 01-02-2013 - 10:10

#6
 Đã gửi 01-02-2013 - 10:15
Đã gửi 01-02-2013 - 10:15

Em là cường anh ạ.Tại sao $\det MN=\det NM$vậy Thắng?????
Vậy là nó không đúng khi 2 cái đó không cùng cấp.
............
@cuong 148
Hi. Anh nhớ nhầm tên. Xin lỗi nha!
Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 01-02-2013 - 11:28
#7
 Đã gửi 01-02-2013 - 14:36
Đã gửi 01-02-2013 - 14:36

Dể dàng kiểm tra được rằng $(AB)^{2}=9(AB)$
Ta có thể viết:
$(BA)^{3}=B.(AB)^{2}.A=9B(AB)A=9(BA)^{2}$
Suy ra $(BA)^{2}(BA-9I_{2})=O$
Nếu $f$ là đa thức tối thiểu của $BA$ thì $f$ là ước của $x^{2}(x-9)$ và $Deg(f)\leq 2$.
(1) Nếu $f=x$ thì $BA=O$ suy ra $AB=O$ vì $O=A(BA)B=(AB)^{2}=9AB$, điều này vô lý.
(2) Nếu $f=x^{2}$ thì $(BA)^{2}=O$ kéo theo $Tr(AB)=Tr(BA)=0$, vô lý
(3) Nếu $f=x(x-9)$ thì $Tr(AB)=Tr(BA)=9$, vô lý.
(4) Nếu $f=x-9$ ta có $BA-9I_{2}=O$. Vậy $BA=9I_{2}$. Đây là kết quả mong muốn.
...............
Nhận xét: Ý tưởng là tìm đa thức tối thiểu f của $BA$. Có 4 khả năng của f thì 3 khả năng đầu là vô lý. Vậy chỉ còn khả năng cuối cùng. Có gì không ổn không ta??
Chổ (2) và (3) có thể sẽ có thắc mắc. Gợi ý là chúng ta sử dụng kết quả sau:
Cho A là ma trận vuông cấp 2 thì đa thức đặc trưng của A là
$f(x)=x^{2}-Tr(A)x+det(A)$
Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 17-03-2014 - 07:13
- cuong148, letrongvan và YeuEm Zayta thích
#8
 Đã gửi 01-02-2013 - 23:22
Đã gửi 01-02-2013 - 23:22

(1) Nếu $f=x$ thì $BA=O$ suy ra $AB=O$ vì $O=A(BA)B=(AB)^{2}=9AB$, điều này vô lý.
(2) Nếu $f=x^{2}$ thì $(BA)^{2}=O$ kéo theo $Tr(AB)=Tr(BA)=0$, vô lý
(3) Nếu $f=x(x-9)$ thì $Tr(AB)=Tr(BA)=9$, vô lý.
(4) Nếu $f=x-9$ ta có $BA-9I_{2}=O$. Vậy $BA=9I_{2}$. Đây là kết quả mong muốn.
...............
Nhận xét: Ý tưởng là tìm đa thức tối thiểu f của $BA$. Có 4 khả năng của f thì 3 khả năng đầu là vô lý. Vậy chỉ còn khả năng cuối cùng. Có gì không ổn không ta??
Nên đổi xét cái 4 lên thay thế cái 2 thì hợp lí hơn.
Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 02-02-2013 - 09:21
#9
 Đã gửi 02-02-2013 - 09:28
Đã gửi 02-02-2013 - 09:28

#10
 Đã gửi 21-03-2013 - 21:57
Đã gửi 21-03-2013 - 21:57

Ta có:
$(NM)^{2}=NMNM=N.\frac{1}{9}(MN)^{2}.M=\frac{1}{9}(NM)^{3}$
Suy ra $NM=9I_{2}$ vì $NM$khả nghịch
.......................
Trong quá trình chứng minh có sử dụng kết quả sau:
"$\forall (A, B, C) \in M_{n,p}(\mathbb{K}) \times M_{p,q}(\mathbb{K}) \times M_{q,r}(\mathbb{K}), rank(ABC) \leq rank(B)$"
Cái này em thấy sai rồi đại ca, $(NM)^{2}=\frac{1}{9}.(NM).(MN).(NM)$ chứ anh! các cái trên thì công nhận,hi
Bài viết đã được chỉnh sửa nội dung bởi letrongvan: 21-03-2013 - 21:59
Tào Tháo
#11
 Đã gửi 22-03-2013 - 01:03
Đã gửi 22-03-2013 - 01:03

#12
 Đã gửi 22-03-2013 - 02:26
Đã gửi 22-03-2013 - 02:26

Tào Tháo
#13
 Đã gửi 22-03-2013 - 08:12
Đã gửi 22-03-2013 - 08:12

#14
 Đã gửi 23-07-2013 - 12:22
Đã gửi 23-07-2013 - 12:22

Sáng nay tiếp cận ý tưởng khác cho bài này. Ý tưởng lấy từ một bài khác trên AoPS. Nhưng cũng phải mất khoảng hơn một giờ đồng hồ để nhận thấy cái đặc biệt của bài toán chúng ta đang xét. Bài này đúng là đẹp thật.
.........................................................
Ta viết M, N dưới dạng ma trận khối.
$M=\begin{pmatrix} X\\ Y \end{pmatrix}$ và $N=\begin{pmatrix} U & V \end{pmatrix}$
Trong đó $X\in M_{1\times 2}(\mathbb{R}),Y\in M_{2\times 2}(\mathbb{R}),U\in M_{2\times 1}(\mathbb{R}),V\in M_{2\times 2}(\mathbb{R})$
Ta có
$MN=\begin{pmatrix} XU & XV\\ UX & YV \end{pmatrix}=\begin{pmatrix} 8 & 2 & -2\\ 2 & 5 & 4\\ -2 & 4 & 5 \end{pmatrix}$
$NM=(UX+VY)=UX+VY$
Suy ra $\left\{\begin{matrix} XU=(8)\\ XV=\begin{pmatrix} 2 & -2 \end{pmatrix}\\ YU=\begin{pmatrix} 2\\ -2 \end{pmatrix}\\ YV=\begin{pmatrix} 5 & 4\\ 4 & 5 \end{pmatrix} \end{matrix}\right.$
Nhận xét rằng $YU.XV=\begin{pmatrix} 4 & -4\\ -4 & 4 \end{pmatrix}$
Suy ra
$YV+YUXV=9I_{2}\Leftrightarrow Y(I_2+UX)V=9I_2$
Từ đây ta suy ra $Y,V$ khả nghịch và
$\left ( (I_2+UX)V \right ).Y=9I_2\Leftrightarrow VY+UXVY=9I_2$
Mặt khác ta cũng có nhận xét rằng $YU.YV.XV=\begin{pmatrix} 4 & -4\\ -4 & 4 \end{pmatrix}$
Suy ra $YUYVXV=YUXV$
Vì $Y,V$ khả nghịch nên ta suy ra $UYVX=UX$
Vậy $NM=UX+VY=UXVY+VY=9I_2$
............................................................
Anh em góp ý thêm nha!
Trong chủ đề này bài toán của ta đã có 3 hướng tiếp cận. Tuy nhiên xem ra cách tiếp cận đầu tiên có lẻ là nhẹ nhàng nhất.
Bài viết đã được chỉnh sửa nội dung bởi vo van duc: 23-07-2013 - 12:22
- phudinhgioihan, YeuEm Zayta và maitram thích
#15
 Đã gửi 27-03-2014 - 09:37
Đã gửi 27-03-2014 - 09:37

Mặt khác ta cũng có nhận xét rằng $YU.YV.XV=\begin{pmatrix} 4 & -4\\ -4 & 4 \end{pmatrix}$
A ơi, chỗ này phép nhân đâu có nghĩa. (2x2) (2x1) (2x2)...
Success is getting what you want
Happiness is wanting what you get
$\LARGE { \wp \theta \eta \alpha \iota -\wp \mu \varsigma \kappa}$
#16
 Đã gửi 27-03-2014 - 23:55
Đã gửi 27-03-2014 - 23:55

A ơi, chỗ này phép nhân đâu có nghĩa. (2x2) (2x1) (2x2)...
$YUXVYV$ anh Đức viết nhầm đấy bạn.
OLP TOÁN SV TRÊN FACEBOOK: http://www.facebook....5/?notif_t=like 
#17
 Đã gửi 14-06-2014 - 13:06
Đã gửi 14-06-2014 - 13:06

0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh