Chủ đề này có 7 trả lời

[ntuan5]

1/ Giải phương trình: $x^3+3x^2-\sqrt[3]{2x+1}=-2x-1$.

2/ Có $2013$ đồng xu, mỗi đồng xu có hai mặt xanh đỏ. Xếp các đồng xu trên bảng sao cho các mặt xanh ngửa lên. Thực hiện lật 4 đồng xu bất kì tùy ý ( có thể đổi mặt xanh thành đỏ thành xanh). Hỏi có thể nhận được kết quả mà tất cả các đồng xu mặt đỏ ngửa lên không?

3/Tìm tất cả hàm $f: Q->Q$ thỏa mãn:
$$f(x+y)=f(x)+f(y)+xy$$

4/a/ Tìm các số nguyên tố thỏa: $(p-1)!+1 \vdots p^2$
b/ CMR tồn tại các số nguyên thỏa:
$$\sum_{1\le i_{1} \le ...\le i_{p-2}\le p-1} \vdots p^2$$

5/ Cho các số thực thỏa mãn: $a,b,c \ge -1$ và$2(a+b+c)+3(ab+bc+ac)+3abc=0$. CMR:
$$\sum \frac{bc+b+c+1}{(a+1)^3(c+2b+3)} \ge 1$$

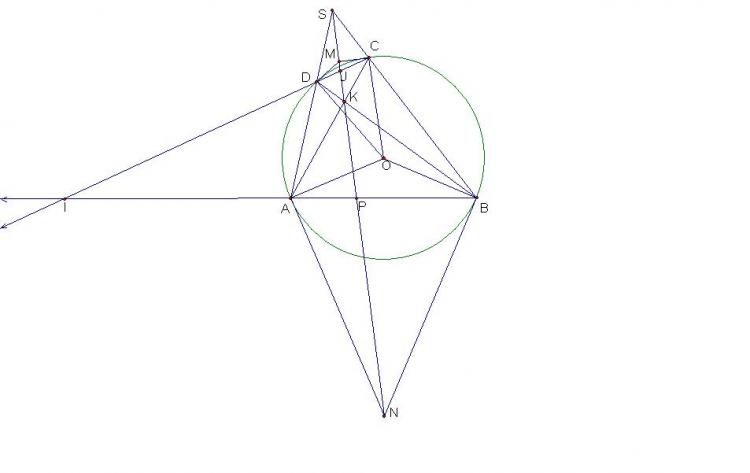
6/ Cho tam giác SAB, đường tròn $(O)$ đi qua A và B cắt các cạnh SB, SA tại C và D. Hai tiếp tuyến với $(O)$ tại A và B cắt nhau tại M, hai tiếp tuyến với $(O)$ tại C;D cắt nhau tại N, AC cắt BD tại K. CMR: 4 điểm M,N,S,K thẳng hàng.

[banhgaongonngon]

1/ Giải phương trình: $x^3+3x^2-\sqrt[3]{2x+1}=-2x-1$.

$x^{3}+3x^{2}+3x+1+x+1=2x+1+\sqrt[3]{2x+1} \Leftrightarrow (x+1)^{3}+(x+1)=\left ( \sqrt[3]{2x+1} \right )^{3}+\sqrt[3]{2x+1} \Leftrightarrow x+1=\sqrt[3]{2x+1} \Leftrightarrow x^{3}+3x^{2}+x=0$

[ilovemath97]

Bài 2: Ta kí hiệu các mặt xanh là 1, mặt đỏ là -1, vậy thì ở trạng thái ban đầu các màu xanh đều ngửa lên nên tích sẽ là 1. Để ý cứ mỗi thao tác lật 4 đồng xu thì tích này ko đổi( đây là đại lượng bất biến). Nên ta có thao tác bao nhiêu lần đi nữa thì tích vẫn sẽ là 1. thế mà nếu xảy ra trạng thái 2013 xu toàn mặt đỏ thì tích sẽ lại là -1, trái với suy luận ở trên. Vậy ta ko bao h nhận đc kết quả 2013 xu toàn mặt đỏ

Bài viết đã được chỉnh sửa nội dung bởi ilovemath97: 24-02-2013 - 16:31

[N H Tu prince]

3/Tìm tất cả hàm $f: Q->Q$ thỏa mãn:
$$f(x+y)=f(x)+f(y)+xy$$

Đặt $g(t)=f(t)-\frac{t^2}{2}=>f(t)=g(t)+\frac{t^2}{2}$ thay vào pt ta được:
$g(x+y)+\frac{(x+y)^2}{2}=g(x)+g(y)+xy+\frac{x^2}{2}+\frac{y^2}{2}$
$=>g(x+y)=g(x)+g(y)=>g(x)=kx,k\in \mathbb{R}=>f(x)=kx+\frac{x^2}{2},k\in \mathbb{R}$

Bài viết đã được chỉnh sửa nội dung bởi hoangngocbao1997: 24-02-2013 - 17:21

[ilovemath97]

bài 6 hình học: Kéo dài $CD$, nó cắt $AB$ tại $I$
Gọi $J,P$ lần lượt là giao điểm của $SK$ với $CD$ và $AB$

Ta có đường đối cực của $M$ là $CD$ qua $I$, nên đường đối cực của $I$ qua $M$

Ta sẽ chứng minh $SK$ chính là đường đối cực của $I$ để suy ra $S,K,M$ thẳng hàng

Thật vậy, có $(IPAB)=-1$ nên đường đối cực của $I$ qua $P$

Qua phép chiếu xuyên tâm $S$ ta có $(IJDC)=-1$ nên đường đối cực của $I$ qua $J$

Do đó $PJ$ chính là đường đối cực của $I$ hay $SK$ chính là đường đối cực của $I$

Như thế ta đã hoàn tất chứng minh $S,K,M$ thẳng hàng

Và vì điểm $M,N$ có vai trò giống nhau trong đường tròn, nên hoàn toàn tương tự, ta cũng đi đến $S,K,N$ thẳng hàng

Vậy, $S,K,M,N$ thẳng hàng(đpcm) và đặc biệt 4 điểm ấy nằm trên đường đối cực của $I$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi ilovemath97: 24-02-2013 - 17:43

[ntuan5]

Bài hình mình làm giống hệt, tiếc là mò cái c/m cực đối cực mất thời gian quá. Bài số khá khó chịu.

[Sagittarius912]

1/ Giải phương trình: $x^3+3x^2-\sqrt[3]{2x+1}=-2x-1$.

Đặt $\sqrt[3]{2x+1}=y+1$
khi đó ta có hệ
$\left\{\begin{matrix} x^{3}+3x^{2}+2x-y=0\\ y^{3}+3y^{2}+3y-2x=0 \end{matrix}\right.$
Trừ 2 vế của pt trên ta có
$x^{3}-y^{3}+3(x^{2}-y^{2})+4(x-y)=0\Rightarrow ...$

[Sagittarius912]

5/ Cho các số thực thỏa mãn: $a,b,c \ge -1$ và$2(a+b+c)+3(ab+bc+ac)+3abc=0$. CMR:
$$\sum \frac{bc+b+c+1}{(a+1)^3(c+2b+3)} \ge 1$$

Đặt

$a+1=x$

$b+1=y$

$c+1=z$

$\Rightarrow x,y,z \ge 0$

Ta có

$xyz=(a+1)(b+1)(c+1)=abc+1+(a+b+c)+(ab+bc+ca)$

nên

$2(a+b+c)+3(ab+bc+ac)+3abc=0$

$\Leftrightarrow 3xyz-(a+b+c+1+1+1)=0$

$\Leftrightarrow x+y+z=3xyz$

$\Leftrightarrow \frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=3$ (1)

BĐT cần chứng minh là

$\sum \frac{bc+b+c+1}{(a+1)^3(c+2b+3)} \ge 1$

$\Leftrightarrow \sum \frac{(b+1)(c+1)}{(a+1)^3[c+1+2(b+1)]} \ge 1$

$\Leftrightarrow \sum \frac{yz}{x^{3}(y+2z)} \ge 1$

$\Leftrightarrow \sum \frac{yz}{x^{2}(yx+2zx)} \ge 1$ (2)

Lại đặt tiếp

$\frac{1}{xy}=m$

$\frac{1}{yz}=n$

$\frac{1}{zx}=p$

Khi đó từ (1) ta có

$m+n+p=3$

$x^{2}=\frac{n}{mp}$

$y^{2}=\frac{p}{mn}$

$z^{2}=\frac{m}{np}$

(1) được viết lại thành

$\sum \frac{m^{2}p^{2}}{n^{2}(p+2m)}\ge 1$

Sử dụng Cauchy-Schwarz ta có

$\sum \frac{m^{2}p^{2}}{n^{2}(p+2m)}=\sum \frac{m^{4}p^{4}}{m^{2}n^{2}p^{2}(p+2m)}\geq \frac{(m^{2}n^{2}+n^{2}p^{2}+p^{2}m^{2})^{2}}{3.m^{2}n^{2}n^{2}(m+n+p)}$

Mặt khác ta có

$(m^{2}n^{2}+n^{2}p^{2}+p^{2}m^{2})\geq mnp(m+n+p)$

$\Rightarrow (m^{2}n^{2}+n^{2}p^{2}+p^{2}m^{2})^{2}\geq m^{2}n^{2}p^{2}(m+n+p)^{2}=3m^{2}n^{2}p^{2}(m+n+p)$

$\Rightarrow \frac{(m^{2}n^{2}+n^{2}p^{2}+p^{2}m^{2})^{2}}{3.m^{2}n^{2}n^{2}(m+n+p)} \geq 1$

$\Rightarrow$ đ.p.c.m

Dấu = xảy ra khi $m=n=p=1$ $\Leftrightarrow a=b=c=0$

Bài viết đã được chỉnh sửa nội dung bởi doandat97: 25-02-2013 - 01:33