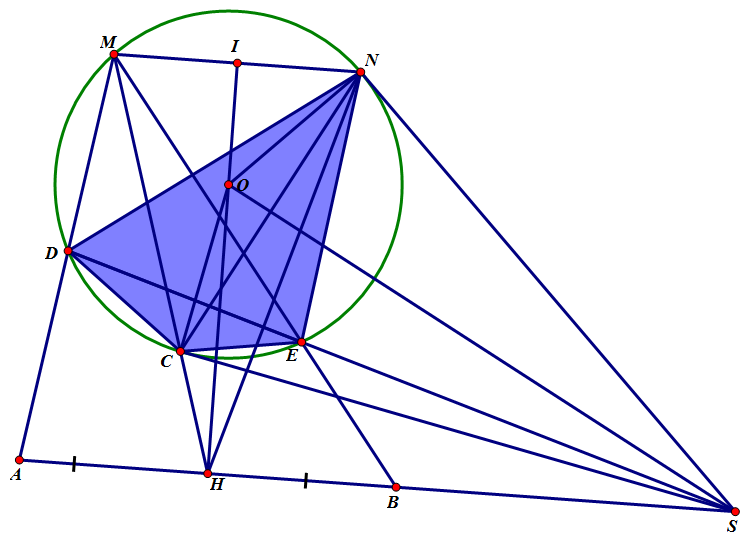
Cho đường tròn $(O)$ và đường thẳng $d$. Gọi $H$ là hình chiếu của $O$ lên $d$. Cho 2 điểm $A,B \in d$ sao cho $HA =HB$. Lấy $M$ bất kì trên $(O)$. $MH,MA,MB$ lần lượt cắt $(O)$ tại $C,D,E$. Gọi $S$ là giao điểm của d và $DE$. Chứng minh $SC$ là tiếp tuyến của đường tròn $(O)$.
#1
 Đã gửi 01-06-2013 - 15:17
Đã gửi 01-06-2013 - 15:17

$P_{G}(\sigma_{1},\sigma_{2},\cdots,\sigma_{n})=\frac{1}{|G|}\sum_{\tau\in G}ind(\tau)$
#2
 Đã gửi 01-06-2013 - 16:00
Đã gửi 01-06-2013 - 16:00

Cho đường tròn $(O)$ và đường thẳng $d$. Gọi $H$ là hình chiếu của $O$ lên $d$. Cho 2 điểm $A,B \in d$ sao cho $HA =HB$. Lấy $M$ bất kì trên $(O)$. $MH,MA,MB$ lần lượt cắt $(O)$ tại $C,D,E$. Gọi $S$ là giao điểm của d và $DE$. Chứng minh $SC$ là tiếp tuyến của đường tròn $(O)$.
Qua $M$ vẽ đường thẳng song song với $d$,Cắt $(O)$ tại $N$,cắt $OH$ tại $I$.
Vì $HA=HB$ và $MN//AB$ nên $M(AB,HN)=-1$,Chiếu chùm điều hòa lên $(O)$ ta có tứ giác $DCEN$
điều hòa.Do đó tiếp tuyến tại $C$ và $N$ đồng quy trên $DE$.(1)
Mặt khác ta có $\widehat{MCN}=\widehat{ION}$ nên $\widehat{NCH}=\widehat{NOH}$.Suy ra 4 điểm
$N,O,C,H$ thuộc một đường tròn.
Gọi $S'$ là giao hai tiếp tuyến tại $C,N$ thì ta có $O,C,S',N$ đồng viên.Suy ra $O,C,N,H,S'$ đồng
viên.Suy ra $\widehat{OHS'}=\widehat{OCS'}=90^{\circ}$.Nên $S'\in AB$.
Lại có theo (1) thì $S'\in DE$.Vậy $S'$ trùng $S$.Vậy ta có DPCM.
- perfectstrong, Stranger411, hoangkkk và 1 người khác yêu thích
#3
 Đã gửi 01-06-2013 - 16:36
Đã gửi 01-06-2013 - 16:36

Bài toán khá hay đó bạn:
Qua $M$ vẽ đường thẳng song song với $d$,Cắt $(O)$ tại $N$,cắt $OH$ tại $I$.
Vì $HA=HB$ và $MN//AB$ nên $M(AB,HN)=-1$,Chiếu chùm điều hòa lên $(O)$ ta có tứ giác $DCEN$
Kí hiệu mà bạn dùng chỗ nào là thế nào vậy ?
mình xem lại lí thuyết về chùm điều hòa mà không thấy.
$P_{G}(\sigma_{1},\sigma_{2},\cdots,\sigma_{n})=\frac{1}{|G|}\sum_{\tau\in G}ind(\tau)$
#4
 Đã gửi 01-06-2013 - 17:23
Đã gửi 01-06-2013 - 17:23

Kí hiệu mà bạn dùng chỗ nào là thế nào vậy ?
mình xem lại lí thuyết về chùm điều hòa mà không thấy.
Có nghĩa là $MA,MB,MH,MN$ là một chùm điều hòa ấy bạn.Cái này trong tài liệu chuyên toán hình học 10 có mà bạn.
#5
 Đã gửi 01-06-2013 - 17:28
Đã gửi 01-06-2013 - 17:28

Qua $M$ vẽ đường thẳng song song với $d$,Cắt $(O)$ tại $N$,cắt $OH$ tại $I$.
Vì $HA=HB$ và $MN//AB$ nên $M(AB,HN)=-1$
Theo mình thấy chỗ này nên chứng minh lại bổ đề sau:
Bổ đề 1: Cho $a,b,c,d$ là chùm đường thẳng tâm $O$. Đường thẳng $\delta$ không đi qua $O$, cắt $a,b,c,d$ tại $A,B,C,D$. Đường thẳng $\delta'$ không đi qua $O$, cắt $a,b,c$ tại $A',B',C'$. Khi đó $\delta' // d$ thì $(ABCD)=(A'B'C')$.
Áp dụng bổ đề trên thì $M(ABHN)= (ABH) = -1$.
Bài viết đã được chỉnh sửa nội dung bởi Stranger411: 01-06-2013 - 17:34
- hoangkkk và nguyenthehoan thích
$P_{G}(\sigma_{1},\sigma_{2},\cdots,\sigma_{n})=\frac{1}{|G|}\sum_{\tau\in G}ind(\tau)$
#6
 Đã gửi 01-06-2013 - 17:31
Đã gửi 01-06-2013 - 17:31

Theo mình thấy chỗ này nên chứng minh lại 2 bổ đề như sau:
Bổ đề 1: Cho $a,b,c,d$ là chùm đường thẳng tâm $O$. Đường thẳng $\delta$ không đi qua $O$, cắt $a,b,c,d$ tại $A,B,C,D$. Đường thẳng $\delta'$ không đi qua $O$, cắt $a,b,c$ tại $A',B',C'$. Khi đó $\delta' // d$ thì $(ABCD)=(A'B'C')$.
Bổ đề 2: Xét 2 chùm $O(ABCO')$ và $O'(ABCO)$. Khi đó $A,B,C$ thẳng hàng thì $O(ABCO') = O'(ABCO)$Áp dụng 2 bổ đề thì $M(ABHN)= N(ABHM) = (ABH) = -1$.
Cái này thi được dùng luôn mà bạn!!!
#7
 Đã gửi 01-06-2013 - 21:52
Đã gửi 01-06-2013 - 21:52

Đúng là cái NguyenTheHoan nói là được dùng
#8
 Đã gửi 01-06-2013 - 22:01
Đã gửi 01-06-2013 - 22:01

Cách của nguyenthehoan đúng như chưa tổng quát đâu ![]() Một cách khác
Một cách khác ![]()
Lời giải 2:
Gọi $F$ là giao điểm còn lại của $HD$ và $(O)$. $FC$ cắt $d$ tại $B'$. Ta chứng minh $B' \equiv B$.
Thật vậy, đường thẳng qua $M$ song song với $d$ cắt $(O)$ tại $J$ khác $M$. Dễ thấy $J,M$ đối xứng qua $OH$. (*)
Ta lại có:\[
\left( {HB';HJ} \right) \equiv \left( {JM;JH} \right) \equiv - \left( {MJ;MH} \right) \equiv \left( {MC;MJ} \right) \equiv \left( {FC;FJ} \right) \equiv \left( {FB';FJ} \right)\left( {\bmod \pi } \right)
\]
Từ đây suy ra $J,F,H,B'$ đồng viên. Nên\[
\left( {B'H;B'J} \right) \equiv \left( {FH;FJ} \right) \equiv \left( {FD;FJ} \right) \equiv \left( {MD;MJ} \right) \equiv \left( {AH;AM} \right)\left( {\bmod \pi } \right)
\]
Từ (*) suy ra $B',A$ đối xứng quay $OH$. Do đó $B' \equiv B \Rightarrow F,C,B$ thẳng hàng.
Gọi $S'$ là giao điểm của tiếp tuyến tại $C$ của $(O)$ và $DE$.
Áp dụng định lý Pascal cho bộ 6 điểm $(C;C;M;E;D;F)$ suy ra $S',H,B$ thẳng hàng.
Điều này đồng nghĩa với $SC$ là tiếp tuyến của $(O)$.
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 01-06-2013 - 22:02
- Trần Đức Anh @@, Stranger411, hoangkkk và 3 người khác yêu thích
$$\text{LOVE}\left( x \right)|_{x = \alpha}^\Omega = + \infty $$
I'm still there everywhere.
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: hình học

|
Chứng minh PQ.CB=DC.QN và O là trung điểm của PQ.Bắt đầu bởi nonamebroy, Hôm qua, 10:24 |
|

|
|

|
Chứng minh tứ giác MAOB nội tiếp đường tròn.Bắt đầu bởi Phuockq, 07-04-2024 |
|

|
|

|
Toán thi Học sinh giỏi và Olympic →
Hình học →
Chứng minh B,M,N,C đồng viênBắt đầu bởi VGNam, 22-02-2024 |
|

|
|

|
Chứng minh ba điểm E, F, H thẳng hàng.Bắt đầu bởi Saturina, 16-02-2024 |
|

|
|

|
Toán thi Học sinh giỏi và Olympic →
Hình học →
a) Chứng minh rằng K thuộc đường tròn đường kính BC . b) Chứng minh rằng IMC KGJ 45oBắt đầu bởi Saturina, 16-02-2024 |
|

|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh