Naix

Trong bài viết mà bạn dẫn chỉ dẫn lại và bổ đề không chứng minh và lời giải bài đó thôi. Minh muốn hỏi về cách chứng minh bổ đề ấy. Cảm ơn bạn

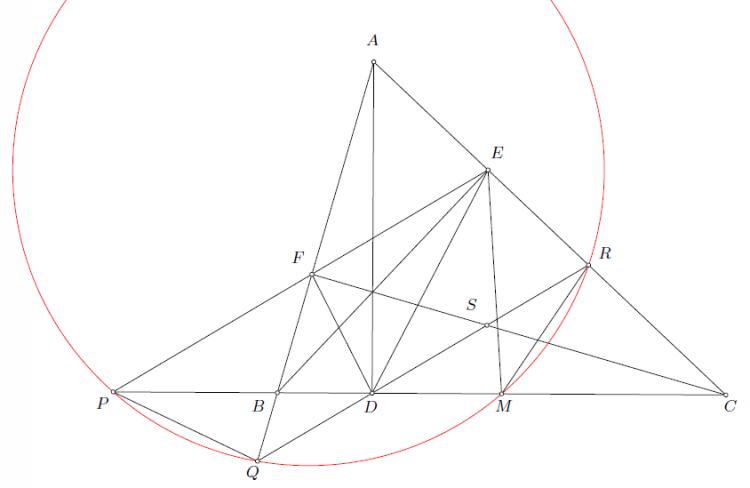
Thực ra bài này dùng bổ đề trên là không cần thiết và phức tạp, có thể biến đổi góc gọn hơn như sau (bạn tự nhìn hình ở trên)

\[\angle LBQ+\angle LQB=\angle KBA+\angle LKC=\angle KBA+\angle LKQ+\angle QKC\] Với chú ý rằng $\angle QKC=\angle QPC=\angle BAK,$ từ đó \[ \angle LBQ+\angle LQB=\angle KBA+\angle KAB+\angle LKQ=\angle BKQ\] Do đó $\angle BKQ+\angle BMQ=180^{\circ}$ suy ra đpcm.

Đường tròn (I) nội tiếp tam giác ABC tiếp  xúc BC, CA,AB tại D, E, F.Vẽ đường kính EH,FK.HK cắt BC tại P;M là trung điểm BC. CMR:$\widehat{IPM}=90^{\circ}$

 

 

Gọi $N$ là trung điểm của $HK.$

Ta có \[\angle IBC=\angle IFD=\angle DHK,\ \angle ICB=\angle IED=\angle DKH \Rightarrow \triangle BIC \sim \triangle HDK\]

Với chú ý rằng $M, N$ lần lượt là trung điểm $BC, HK$ suy ra $\triangle DNH \sim \triangle IMB \Rightarrow \angle IMB=\angle DNH.$

Dễ thấy $\angle INP=\angle IDP=90^{\circ}$ suy ra $INDP$ nội tiếp, thành thử \[ \angle IMB=\angle DNH =\angle DNP=\angle DIP \Rightarrow \angle MIP=90^{\circ}\]

Bài 22 (Đề thi vào chuyên toán THPT chuyên Vĩnh Phúc 2013-2014):

Cho tam giác $ABC$ nhọn $(AB<AC).$ Gọi $D,E,F$ lần lượt là chân các đường cao hạ từ $A,B,C.$ Gọi $P=BC\cap EF.$ Đường thẳng qua $D$ song song với $EF$ cắt $AB,AC,CF$ lần lượt tại $Q,R,S.$ Chứng minh rằng: 

 a) Tứ giác $BQCR$ nội tiếp.

 b) $D$ là trung điểm của $QS.$

 c) $(PQR)$ chia đôi $BC.$

 

 

a, Vì $EF \parallel RQ$ nên $\angle BQR=\angle AFE=\angle RCB$ suy ra $BQCR$ nội tiếp.

 

b, Dễ thấy $EB, EC$ lần lượt là phân giác trong và phân giác ngoài đỉnh $E$ của tam giác $EDP,$ do đó 

\[\frac{BD}{BP}=\frac{ED}{EP}=\frac{CD}{CP}\]

Chú ý rằng $QS \parallel PF$ nên theo Thales $\frac{DQ}{PF}=\frac{BD}{BP}=\frac{CD}{CP}=\frac{DS}{PF},$ thành thử $DQ=DS.$

 

c, Gọi $M$ là trung điểm của $BC,$ ta có $EMDF$ nội tiếp, từ đó $\triangle PDF \sim \triangle EDM \mbox{ (g.g)}$ suy ra $DP.DM=DE.DF$

Ta có $\angle DQF=\angle AFE =\angle DFQ$ suy ra $DQ=DF,$ tương tự $DE=DR.$

Bởi vậy $DP.DM=DE.DF=DQ.DR$ suy ra $PQMR$ nội tiếp hay $(PQR)$ đi qua $M.$

 

Mình đề nghị bài tiếp theo cũng là do mình chế, khá phù hợp với các bạn cấp 2 ôn thi:

Bài 26: Cho tam giác $ABC$ nội tiếp $(O)$. Một đường tròn $(K)$ qua $B,C$ cắt $AB,AC$ tại $E,F$. Một đường thẳng $d$ qua $A$ sao cho $d$ cắt $(O),(AEF)$ lần lượt lại $M,N$. Chứng minh rằng: $KM=KN$.

 

 

Gọi $I$ là tâm đường tròn ngoại tiếp tam giác $AEF.$

Ta có $\angle OAC+\angle AFE=\angle OAC+\angle ABC=90^{\circ}$ suy ra $OA \perp EF,$ tương tự cũng có $IA \perp BC.$

 Theo tính chất đường nối tâm thì $IK \perp EF, OK \perp BC$ do đó $AIKO$ là một hình bình hành, bởi vậy 

\[IN=IA=OK,\ IK=OA=OM\]

 Chú ý rằng $\triangle ENF \sim \triangle BMC \mbox{ (g.g)}$ nên sử dụng biến đổi góc thu được $\angle NIK =\angle KOM,$ thành thử $\triangle NIK =\triangle KOM \mbox{ (c.g.c)}$ suy ra $KM=KN.$

Cho tứ giác $ABCD$ nội tiếp đường tròn $(O), AB$ cắt $CD$ tại $E, AD$ cắt $BC$ tại $F.$ Lấy $M$ thuộc $(O), EM, FM$ cắt $(O)$ lần lượt tại $I, J.$ Chứng minh $AC, BD, IJ$ đồng quy.

Bài toán 3: Cho hàm số $f(x)$ khả vi hai lần trên $R$ với $f''$ liên tục trên $[0,1]$ sao cho : $\displaystyle \int_{0}^{1}f(x)dx=2 \displaystyle \int_{\dfrac{1}{4}}^{\dfrac{3}{4}}f(x)dx$ Chứng minh rằng tồn tại $x_0$ thuộc $(0, 1)$ sao cho : $f''(x_0)=0$.


P/s : Bài này phải dùng Lagrange để giải nhưng mình chưa biết chọn hàm số phù hợp, mong các bạn thảo luận bài toán này.