pnhungqt

Mình giải ngắn thôi nhé.
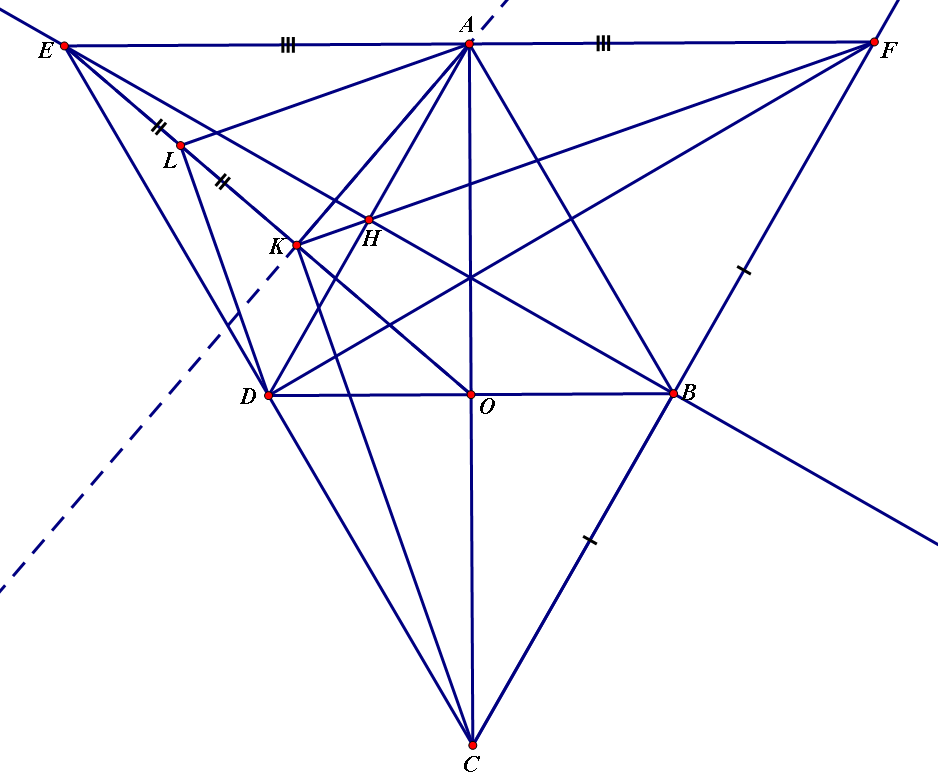
Dễ thấy CEF là tam giác đều và A, D, B là trung điểm các cạnh của nó. Nối KC.
Ta có $\Delta AKO\sim \Delta EAO \Rightarrow \frac{KO}{AO}=\frac{KA}{AE}\Rightarrow \frac{KO}{KA}=\frac{AO}{AE}=\frac{OC}{AF}$ (1)
Mà $\widehat{EAK}=\widehat{KOA}$ (cùng phụ góc $\widehat{KAO}$)
$\Rightarrow \widehat{KOC}=\widehat{KAF}$ (2)
Từ (1) và (2) ta có $\Delta KOC\sim \Delta KAF \Rightarrow \widehat{CKO}=\widehat{FKA}$
Do đó $\widehat{CKF}=\widehat{CKO} + \widehat{OKF}=\widehat{FKA} + \widehat{OKF}=\widehat{OKA}=90^{\circ}$
Mặt khác dễ thấy $AL\parallel FK, DL\parallel CK\Rightarrow \widehat{ALD}=\widehat{CKF}=90^{\circ}$
Do đó $AL\perp LD\Rightarrow FK\perp LD$

Bài toán 2.
Chứng minh với mọi số thực dương $a,b,c$ thoả mãn $a+b+c=3$ ta luôn có:
$$\frac{a^2(b+c)}{bc}+\frac{b^2(a+c)}{ac}+\frac{c^2(a+b)}{ab}\geq 6$$

Cách khác:
Ta có: $(b+c)^{2}\geq 4bc\Rightarrow \frac{b+c}{bc}\geq \frac{4}{b+c}\Rightarrow \frac{a^{2}(b+c)}{bc}\geq \frac{4a^{2}}{b+c}$
Vậy nên $\frac{a^2(b+c)}{bc}+\frac{b^2(a+c)}{ac}+\frac{c^2(a+b)}{ab}\geq\frac{4a^{2}}{b+c}+\frac{4b^{2}}{a+c}+\frac{4c^{2}}{b+a}$
Mà theo BĐT Cauchy-Schwarz ta có $\frac{4a^{2}}{b+c}+\frac{4b^{2}}{a+c}+\frac{4c^{2}}{b+a}\geq \frac{(2a+2b+2c)^{2}}{2a+2b+2c}= 2(a+b+c)=6$
Vậy BĐT được chứng minh
Dấu đẳng thức xảy ra khi a=b=c=1

Bài 122 : (Đề thi Trường Sư Phạm Thực Hành Tp.HCM năm 2012 - 2013)
Cho ∆ ABC vuông tại A ( AB < AC ), có đường cao AH và O là trung điểm BC. Đường tròn tâm I đường kính AH cắt AB, AC lần lượt tại M và N.
1) Chứng minh rằng :

a) AM.AB = AN.AC

b) Tứ giác BMNC nội tiếp.

2) Gọi D là giao điểm của OA và MN. Chứng minh rằng :
a) Tứ giác ODIH nội tiếp.

b) $\frac{1}{{AD}} = \frac{1}{{HB}} + \frac{1}{{HC}}$

3) Gọi P là giao điểm của đường thẳng MN và đường thẳng BC. Đường thẳng AP cắt đường tròn đường kính AH tại điểm K ( khác A ). Tính góc ∠BKC.
4) Cho AB = 6, AC = 8. Hãy tính bán kính của đường tròn ngoại tiếp tam giác BMN.

2)b)
Vì AH là đường kính đường tròn tâm I nên:$\widehat{AMH}=\widehat{ANH}=90^{\circ}$$\Rightarrow MH\perp AB;HN\perp AC$
Tam giác AHC vuông tại H có HN là đường cao nên: $\frac{1}{HN^{2}}=\frac{1}{AH^{2}}+\frac{1}{HC^{2}}$
Tam giác AHB vuông tại H có HM là đường cao nên: $\frac{1}{HM^{2}}=\frac{1}{AH^{2}}+\frac{1}{HB^{2}}$
Do đó$\frac{1}{HN^{2}}+\frac{1}{HM^{2}}=\frac{2}{AH^{2}}+\frac{1}{HC^{2}}+\frac{1}{HB^{2}}$ (1)
Mặt khác tứ giác AMHN có $\widehat{AMH}=\widehat{ANH}=\widehat{BAC}=\widehat{MAN}=90^{\circ}$ nên là hình chữ nhật, do đó MH=AN; NH=AM (2)
Lại có Tam giác ABC vuông tại A có AH là đường cao nên: $AH^{2}=HB.HC$ (3)
Từ (1)(2)(3) ta có: $\frac{1}{AN^{2}}+\frac{1}{AM^{2}}=\frac{2}{HB.HC}+\frac{1}{HC^{2}}+\frac{1}{HB^{2}}=(\frac{1}{HB}+\frac{1}{HC})^{2}$
Mặt khác tam giác AMN có AD vuông góc với MN (theo câu trên) nên $\frac{1}{AD^{2}}=\frac{1}{AM^{2}}+\frac{1}{AN^{2}}$
Vậy $\frac{1}{AD^{2}}=(\frac{1}{HB}+\frac{1}{HC})^{2}$ hay$\frac{1}{AD}=\frac{1}{HB}+\frac{1}{HC}$
3)
Tứ giác BMNC nội tiếp nên $\widehat{MBC}=\widehat{MNA}$ (cùng bù với góc MNC)
Tứ giác KMNA nội tiếp nên $\widehat{PKM}=\widehat{MNA}$ (cùng bù với góc KMN)
Do đó $\widehat{MBC}=\widehat{PKM}$ $\Rightarrow \widehat{PKM}+\widehat{PBM}=\widehat{MBC}+\widehat{PBM}=180^{\circ}$
Cho nên Tứ giác BPKM nội tiếp, suy ra $\widehat{PKB}=\widehat{PMB}$ (cùng chắn cung PB)
Lại có Tứ giác BMNC nội tiếp nên $\widehat{PMB}=\widehat{NCB}$ (cùng bù với góc BMN)
Do đó $\widehat{PKB}=\widehat{NCB}$ hay $\widehat{PKB}=\widehat{ACB}$$\Rightarrow \widehat{ACB}+\widehat{AKB}=\widehat{PKB}+\widehat{AKB}=180^{\circ}$
Cho nên Tứ giác BKAC nội tiếp, suy ra $\widehat{BKC}=\widehat{BAC}=90^{\circ}$ (cùng chắn cung BC)
Vậy $\widehat{BKC}=90^{\circ}$
4) Do tứ giác BMNC nội tiếp nên đường tròn ngoại tiếp tam giác BMN cũng là đường tròn ngoại tiếp tứ giác BMNC. Cho nên bán kính đường tròn ngoại tiếp tam giác BMN cũng là bán kính đường tròn ngoại tiếp tứ giác BMNC.
Gọi S là tâm đường tròn ngoại tiếp tứ giác BMNC thì S cũng là tâm đường tròn ngoại tiếp tam giác BMN.
Vì S là tâm đường tròn ngoại tiếp tứ giác BMNC mà O là trung điểm của BC nên $SO\perp BC$
Lại có $AH\perp BC$ nên $SO\parallel AH\Rightarrow SO\parallel AI$ (4)
Mặt khác AMHN là hình chữ nhật có I là trung điểm của AH nên I là trung điểm của MN do đó $SI\perp MN$ (Vì S là tâm đường tròn ngoại tiếp tứ giác BMNC) mà theo câu 2)a) ta có $AO\perp MN$
Do đó $SI\parallel AO$ (5)
Từ (4)(5) ta có AISO là hình bình hành $\Rightarrow SI=AO$
Vậy Áp dụng định lí Pythagore ta có
$SN^{2}=SI^{2}+IN^{2}=AI^{2}+AO^{2}=(\frac{AH}{2})^{2}+(\frac{BC}{2})^{2}=\frac{BC^{2}+AH^{2}}{4}$
Mặt khác tam giác ABC vuông tại A có AH là đường cao, AB=6, AC=8 nên:
$BC^{2}=AB^{2}+AC^{2}=6^{2}+8^{2}=100; AH^{2}=\frac{AB^{2}.AC^{2}}{BC^{2}}=\frac{6^{2}.8^{2}}{100}=\frac{576}{25}$
Vậy $SN^{2}=\frac{BC^{2}+AH^{2}}{4}=\frac{769}{25}$$\Rightarrow SN=\frac{\sqrt{769}}{5}$
Vậy bán kính đường tròn ngoại tiếp tam giác BMN là $\frac{\sqrt{769}}{5}$

Bài178 choa,b,c>0 a² +b² +c²=3. Tìm min P

P=$\frac{a^3{}}{\sqrt[3]{a+3b}}+\frac{b^3{}}{\sqrt[3]{b+3c}}+\frac{c^3{}}{\sqrt[3]{c+3a}}$

Lời giải:
Ta có Theo BĐT Cauchy:
$\sqrt[3]{16}.\sqrt[3]{a+3b}=\sqrt[3]{4.4.(a+3b)}\leq \frac{a+3b+8}{3}\Leftrightarrow \sqrt[3]{a+3b}\leq \frac{a+3b+8}{3\sqrt[3]{16}}$$\Leftrightarrow \frac{a^{3}}{\sqrt[3]{a+3b}}\geq \frac{3\sqrt[3]{16}.a^{3}}{a+3b+8}=\frac{3\sqrt[3]{16}.a^{4}}{a^{2}+3ab+8a}$
Tương tự ta cũng có các BĐT:$\frac{b^{3}}{\sqrt[3]{b+3c}}\geq \frac{3\sqrt[3]{16}.b^{4}}{b^{2}+3bc+8b}$ và $\frac{c^{3}}{\sqrt[3]{c+3a}}\geq \frac{3\sqrt[3]{16}.c^{4}}{c^{2}+3ca+8c}$
Vậy theo BĐT Cauchy-Schwarz ta có:
$P=\sum \frac{a^{3}}{\sqrt[3]{a+3b}}\geq \sum \frac{3\sqrt[3]{16}.a^{4}}{a^{2}+3ab+8a}\geq 3\sqrt[3]{16}.\frac{(a^{2}+b^{2}+c^{2})^{2}}{a^{2}+b^{2}+c^{2}+3(ab+bc+ca)+8(a+b+c)}$
Mặt khác áp dụng BĐT Cauchy-Schwarz cho các bộ 3 số ta có:
$3(ab+bc+ca)\leq 3(a^{2}+b^{2}+c^{2})$
$8(a+b+c)\leq 8\sqrt{(1^{2}+1^{2}+1^{2})(a^{2}+b^{2}+c^{2})}=8\sqrt{3.3}=24$
Vậy $P\geq 3\sqrt[3]{16}.\frac{(a^{2}+b^{2}+c^{2})^{2}}{4(a^{2}+b^{2}+c^{2})+24}=\frac{3\sqrt[3]{16}.9}{4.3+24}\doteq \frac{3\sqrt[3]{2}}{2}$
Dấu đẳng thức xảy ra khi và chỉ khi $a=b=c=1$
Vậy $Min P=\frac{3\sqrt[3]{2}}{2}$ tại $a=b=c=1$

Bài 116:
Cho đường tròn (O;R) và tam giác cân ABC (AB=AC>R) có ba đỉnh nằm trên đường tròn đó. Kẻ đường kính AI. Gọi M là điểm bất kỳ trên cung nhỏ AC.Mx là tia đối của tia MC.Trên tia đối MB lấy một điểm D sao cho MD=MC
a/ Chứng minh rằng tia MA là tia phân giác của góc BMx
b/ Gọi K là giao điểm thứ 2 của đường thằng DC với đường tròn (O;R).Từ giác MIDK là hình gì?
c/ Tìm quỹ tích của D khi M di động trên cung nhỏ AC

Lời giải:

a/ Ta có:
$\widehat{AMB}=\widehat{ACB}$ ( cùng chắn cung AB của (O))mà $\widehat{ABC}=\widehat{ACB}$ (tam giác ABC cân tại A)
$\Rightarrow \widehat{AMB}=\widehat{ABC}$
Lại có: $\widehat{AMx}+\widehat{AMC}=180^{\circ}$ (2 góc kề bù); $\widehat{ABC}+\widehat{AMC}=180^{\circ}$ (ABCM nội tiếp)
Do đó $\widehat{AMx}=\widehat{ABC}$
Vậy $\widehat{AMB}=\widehat{AMx}$ nên MA là tia phân giác góc BMx
b/(ở đây là MIKD mới phải)
Ta có tam giác MCD cân tại M (MC=MD) nên $\widehat{MDC}=\widehat{MDK}=\widehat{MCK}$
Mà $\widehat{MCK}=\widehat{MIK}$ (cùng chắn cung KM)
Do đó :$\widehat{MDK}=\widehat{MIK}$ (1)
Mặt khác tam giác ABC cân tại A nội tiếp đường tròn (O) nên AO là tia phân giác góc BAC mà AI là đường kính nên AI là tia phân giác góc BAC. Do đó $\widehat{BAI}=\widehat{CAI}$
Suy ra cung BI và cung CI bằng nhau $\Rightarrow \widehat{BMI}=\widehat{IKC}$
Lại có: $\widehat{BMI}+\widehat{DMI}=180^{\circ}$ (2 góc kề bù); $\widehat{IKC}+\widehat{IKD}=180^{\circ}$ (2 góc kề bù).
$\Rightarrow \widehat{IMD}=\widehat{IKD}$ (2)
Từ (1) và (2) ta có tứ giác MIKD có các góc đối bằng nhau nên là hình bình hành.
c/
Phần thuận: Nối AD.
Ta có do M chuyển động trên cung nhỏ AC nên:
$\widehat{AMC}=\widehat{AMB}+\widehat{BMC};\widehat{AMD}=\widehat{AMx}+\widehat{DMx}$
Mà $\widehat{AMx}=\widehat{AMB}$ (theo câu a) và $\widehat{DMx}=\widehat{BMC}$ (đối đỉnh)
$\Rightarrow \widehat{AMC}=\widehat{AMD}$
Mặt khác $\Delta AMD$ và $\Delta AMC$ có chung cạnh AM và MC=MD
$\Rightarrow \Delta AMD=\Delta AMC \Rightarrow AD=AC$
Vậy D luôn cách điểm A một khoảng bằng AC cố định nên khi M chuyển động trên cung nhỏ AC thì D chuyển động trên đường tròn tâm A bán kính AC.
Mặt khác khi M tới C thì $M\equiv C\equiv D$
khi M tới A thì B, A, D thẳng hàng (do B, M, D thẳng hàng) nên nếu gọi giao điểm của AB và đường tròn tâm A bán kính AC là H thì $D\equiv H$
Vậy khi M chuyển động trên cung nhỏ AC thì D chuyển động trên cung HC của đường tròn tâm A bán kính AC.
Phần đảọ Gọi giao điểm cùa BM với đường tròn tâm A bán kính AC trên cung HC là D' ta chứng minh $$D\equiv D'$$ bằng cách chứng minh $MD'=MD=MC$
Thật vậy nối AD' ta có tam giác ABD' cân tại A $\Rightarrow \widehat{ABD'}=\widehat{AD'B}\Rightarrow \widehat{AD'M}=\widehat{ABM}$
Mà $\widehat{ACM}=\widehat{ABM}$ (cùng chắn cung AM) $\Rightarrow \widehat{AD'M}=\widehat{ACM}$
Ta cũng có tam giác ACD' cân tại A $\Rightarrow \widehat{ACD'}=\widehat{AD'C}$
mà M nằm trên cung nhỏ AC nên $\widehat{ACD'}=\widehat{ACM}+\widehat{MCD'}$ và $\widehat{AD'C}=\widehat{AD'M}+\widehat{MD'C}$
Do đó $\widehat{MCD'}=\widehat{MD'C}$ suy ra tam giác MCD' cân tại M nên MD'=MC=MD $\Rightarrow D\equiv D'$ (do D và D' cùng nằm trên BM)
Kết Luận: Quỹ tích điểm D khi M chuyển động trên cung nhỏ AC là cung HC của đường tròn tâm A bán kính AC

Bài 379: Giúp mình bài tập này với
Cho $\sqrt{a^{2}+b^{2}}+\sqrt{b^{2}+c^{2}}+\sqrt{c^{2}+a^{2}}=\sqrt{2012}$.

Chứng minh rằng :
$\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\geq \frac{1}{2}\sqrt{\frac{2012}{2}}$

Mình có cách khác: Bài này thì a, b, c phải dương
Đặt $x=\sqrt{a^{2}+b^{2}}; y=\sqrt{b^{2}+c^{2}}; z=\sqrt{c^{2}+a^{2}}$$(x,y,z\geq 0)$
Khi đó: $x+y+z=\sqrt{2012}$
Ta có: $b^{2}+c^{2}\geq 2bc \Rightarrow 2(b^{2}+c^{2})\geq (b+c)^{2}$$\Rightarrow2y^{2}\geq(b+c)^{2}\Rightarrow y\sqrt{2}\geq b+c$
Lại có $x^{2}+z^{2}-y^{2}=a^{2}+b^{2}+c^{2}+a^{2}-b^{2}-c^{2}=2a^{2}$$\Rightarrow a^{2}=\frac{x^{2}+z^{2}-y^{2}}{2}$
Do đó $\frac{a^{2}}{b+c}\geq \frac{x^{2}+z^{2}-y^{2}}{2\sqrt{2}y}$
$\Leftrightarrow \frac{a^{2}}{b+c}\geq\frac{1}{2\sqrt{2}}(\frac{x^{2}}{y}+\frac{z^{2}}{y}-y)=\frac{1}{2\sqrt{2}}(\frac{x^{2}}{y}+y+\frac{z^{2}}{y}+y-3y)$
$\Leftrightarrow \frac{a^{2}}{b+c}\geq\frac{1}{2\sqrt{2}}(2x+2z-3y)$ (theo BĐT Cauchy)
Tương tự ta có:$\frac{b^{2}}{c+a}\geq\frac{1}{2\sqrt{2}}(2x+2y-3z)$ và $\frac{c^{2}}{a+b}\geq\frac{1}{2\sqrt{2}}(2y+2z-3x)$
Cộng theo vế các bất đẳng thức trên ta có:
$\frac{a^{2}}{b+c}+\frac{b^{2}}{c+a}+\frac{c^{2}}{a+b}\geq\frac{1}{2\sqrt{2}}(x+y+z)=\frac{1}{2}\sqrt{\frac{2012}{2}}$
Dấu đẳng thức xảy ra khi và chỉ khi:$x=y=z=\frac{\sqrt{2012}}{3}\Rightarrow a=b=c\frac{\sqrt{1006}}{3}$

Nối BE, BF, CE, CF.
TH 1: E nằm giữa A và F
Lấy G đối xứng với E qua AB, H đối xứng với E qua AC, I đối xứng với F qua BC. Nối BG, BI, CI, CH, FG, FH, EI.
Vì G đối xứng với E qua AB nên $\angle GBE = 2\angle ABE$,
vì I đối xứng với F qua BC nên $\angle FBI = 2\angle CBF$.
Mà $\angle ABE = \angle CBF$ (gt) nên $\angle GBE = \angle FBI$.
Do đó: $\angle GBE +\angle EBF = \angle FBI +\angle EBF$.
Hay: $\angle GBF = \angle EBI$ (1)
Lại có : BG=BE (G đối xứng với E qua AB) (2)
BF=BI (I đối xứng với F qua BC) (3)
Từ (1), (2), (3) ta có $\bigtriangleup BGF =\bigtriangleup BEI$ (c.g.c)
Suy ra: FG = EI (4)
Vì G đối xứng với E qua AB nên $\angle GAE = 2\angle BAE = 2\angle BAD$,
vì H đối xứng với E qua AC nên $\angle HAE = 2\angle CAE = 2\angle CAD$.
Mà $\angle BAD = \angle CAD$(do AD là phân giác) nên $\angle GAE = \angle HAE$.
Hay: $\angle GAF = \angle HAF$.
Lại có : AG=AE (G đối xứng với E qua AB)
AH=AE (H đối xứng với E qua AC)
Nên AG=AH
Mà $\bigtriangleup AGF, \bigtriangleup AHF$ có chung cạnh AF
Do đó: $\bigtriangleup AGF =\bigtriangleup AHF$ (c.g.c)
Suy ra: FG=FH (5)
Từ (4), (5) ta có: EI=FH (6)
Ta cũng có: CH=CE (H đối xứng với E qua AC) (7)
CF=CI (I đối xứng với F qua BC) (8)
Từ (6), (7), (8) ta có $\bigtriangleup EIC =\bigtriangleup HFC$ (c.c.c)
Suy ra $\angle HCF = \angle ECI$
$\Rightarrow \angle HEC + \angle ECF = \angle FCI + \angle ECF \Rightarrow \angle HEC = \angle FCI$
Mà $\angle HEC = 2\angle ACE$ (H đối xứng với E qua AC)
$\angle FCI = 2\angle BCF$ (I đối xứng với F qua BC)
Do đó ta suy ra: $\angle ACE = \angle BCF$ (đpcm)
TH 2: F nằm giữa A và E
Ta có:$\angle ABE = \angle CBF$
$\Rightarrow \angle ABF + \angle EBF = \angle CBE + \angle EBF$
$\Rightarrow \angle ABF = \angle CBE$
Đến đây chứng minh như trường hợp 1, ta cũng có điều phải chứng minh
Vậy $\angle ACE = \angle BCF$