Mới có bản Scan thôi, các bạn dùng tạm ![]()
Stranger411
Giới thiệu
.♥ ღ ♥______.♥ ღ ♥
♥______♥__♥______.♥
♥____ღ__I__ღ_____♥
♥.____LOVE____.♥
♥_................._♥
♥_______♥
ღ ♥ ღ
♥
Thống kê
- Nhóm: Thành viên
- Bài viết: 85
- Lượt xem: 5045
- Danh hiệu: Hạ sĩ
- Tuổi: 27 tuổi
- Ngày sinh: Tháng mười một 4, 1996
-
Giới tính
 Nam
Nam
-
Đến từ
Somewhere ...
Công cụ người dùng
Lần ghé thăm cuối
IMO shortlist 2012 - Problems + Solution
09-08-2013 - 15:20
Mở rộng Problem 4 - IMO 2013
08-08-2013 - 14:40
1 bài mở rộng của thầy Quang Hùng trong GGTH lần 5
Cho tam giác $ABC$, đường tròn $(I)$ đi qua $B,C$ cắt CA,AB tại $N,M$ khác $B,C$.
Đặt $H = BN \cap CM$. Gọi $d$ là đường thẳng qua $I$ vuông góc với $AH$. Lấy $W$ bất kì trên $d$.
$WK,WL$ là đường kính của đường tròn ngoại tiếp các tam giác $WBM,WCN$.
Chứng minh $K,H,L$ thẳng hàng.

Chứng minh ba đường tròn đồng quy
27-07-2013 - 13:22
Cho tứ giác toàn phần $ABCDEF$. Chứng minh các đường tròn đướng kính $AC,BD,EF$ đồng quy tại 2 điểm.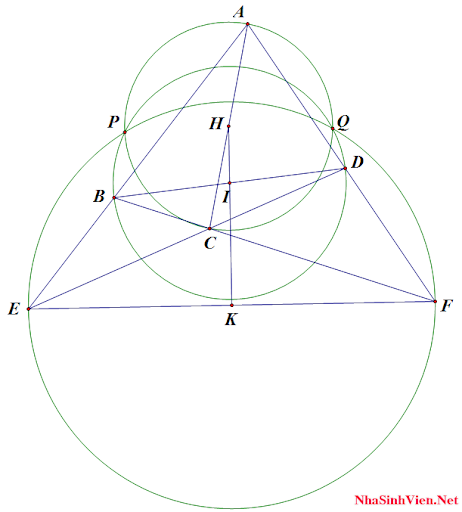
Chứng minh 3 điểm cùng thuộc một đường vuông góc với $OE'$
03-06-2013 - 23:15
Cho tam giác $ABC$ có $O$ là tâm đường tròn ngoại tiếp, $E$ là tâm đường tròn Euler. Lấy $E'$ thỏa $\widehat{E'BA}=\widehat{EBC}$ và $\widehat{E'AB}=\widehat{EAC}$. Trung trực $OA$ cắt $BC$ tại $A'$. Các điểm $B',C'$ được xác định tương tự. Chứng minh $A',B',C'$ cùng thuộc 1 đường thẳng vuông góc với $OE'$
Chứng minh tiếp tuyến
01-06-2013 - 15:17
Cho đường tròn $(O)$ và đường thẳng $d$. Gọi $H$ là hình chiếu của $O$ lên $d$. Cho 2 điểm $A,B \in d$ sao cho $HA =HB$. Lấy $M$ bất kì trên $(O)$. $MH,MA,MB$ lần lượt cắt $(O)$ tại $C,D,E$. Gọi $S$ là giao điểm của d và $DE$. Chứng minh $SC$ là tiếp tuyến của đường tròn $(O)$.
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Chủ đề: Stranger411



 Tìm kiếm
Tìm kiếm









