liverpool29

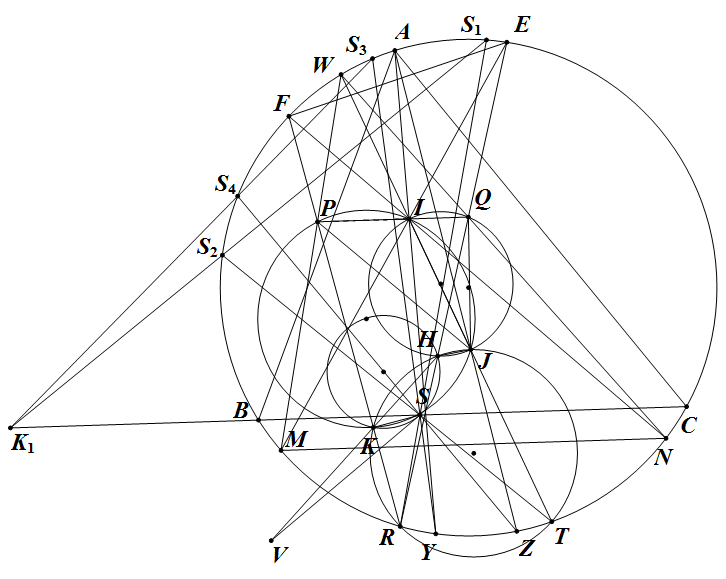
Một mở rộng của bài 6: (xuất phát từ bài mở rộng số 6 của thầy Hùng trong "Lời giải và bình luận VMO 2016")

Cho $\Delta ABC$ nội tiếp $(O)$, có $I,J$ là hai điểm đẳng giác. $AI,AJ$ cắt $(O)$ lần lượt tại $Y,Z$.

$M,N$ thuộc cung $BC$ không chứa $A$ của $(O)$ sao cho $MN \parallel BC$. $IJ$ cắt $(O)$ tại $W,T$ ($W$ thuộc cung chứa $A$).

$d$ là đường thẳng qua $I$ và song song $BC$.

$WM,WN$ cắt $d$ lần lượt tại $P,Q$.

$MI,NI$ cắt $(O)$ lần lượt tại $E,F$.

$FP,EQ$ cắt nhau tại $R$.

$EQ$ cắt $(IJQ)$ tại $H$, $FP$ cắt $(IJP)$ tại $K$.

$a)$ Chứng minh rằng $H,K,R,T,J$ đồng viên.

$b)$ $HK$ đi qua một điểm cố định khi $M,N$ di động. Gọi điểm đó là $V$.

$c)$ Gọi $S$ là điểm thuộc $BC$ sao cho $VH.VK=VS^2$.

$RS,TS$ cắt $(O)$ tại $S_1,S_2$.

$YS,ZS$ cắt $(O)$ tại $S_3,S_4$.

Chứng minh rằng $S_1S_2,S_3S_4,BC$ đồng quy.

 

P/s: Mình xin lỗi, kết luận của câu c đúng với mọi S thuộc BC. Mình sẽ cố gắng làm lại.

Câu hình b chỉ cần để ý $KG \parallel EM, HG \parallel NF, PQ \parallel BC$ và $P,I,Q$ thẳng hàng; biến đổi góc ta có đccm.

Câu 4:
Ta có : $a^2+b^2+c^2=(a+b+c)(a^2+b^2+c^2)=a^3+b^3+c^3+a^2b+b^2 c+c^2a+ab^2+bc^2+ca^2$
Mă t khác theo $AM-GM$:
$a^3+ab^2 \ge 2a^2b; b^3+ bc^2 \ge 2b^2c; c^3+ca^2 \ge 2c^2a$
Suy ra : $a^2+b^2+c^2 \ge 3(a^2b+b^2c+c^2a)$
Suy ra $F \ge 14(a^2+b^2+c^2)+\dfrac{3(ab+bc+ca)}{a^2+b^2+c^2} =14(a^2+b^2+c^2)+\dfrac{3-3(a^2+b^2+c^2)}{a^2+b^2+c^2} (1)$
Đặt $k=a^2+b^2+c^2$
$(1) \Leftrightarrow 14k+\dfrac{\dfrac{3}{2} -\dfrac{3}{2} k}{k}$, với $k \ge \dfrac{1}{3}$
Đến đây dùng Cauchy điểm rơi, hi vọng là ra