dễ dàng ta chứng minh được :GD.GN=GE.GF=GM.GA=> AMNI nội tiếp => NMA=90 độ ,=> N,H,M thằng hàng => H là trực tâm tam giác ANG=> ĐPCM
- yeutoan11, nthoangcute và locnguyen2207 thích
 Bí mật
Bí mật
 Gửi bởi haichau97
trong 03-08-2012 - 15:14
Gửi bởi haichau97
trong 03-08-2012 - 15:14
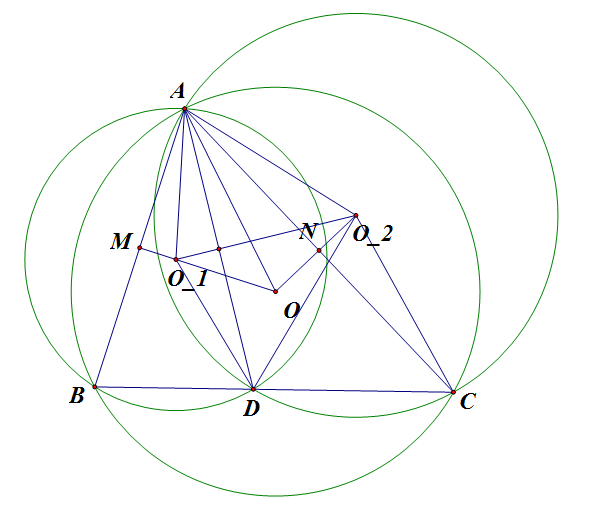
dễ dàng ta chứng minh được :GD.GN=GE.GF=GM.GA=> AMNI nội tiếp => NMA=90 độ ,=> N,H,M thằng hàng => H là trực tâm tam giác ANG=> ĐPCM
 Gửi bởi haichau97
trong 28-07-2012 - 12:19
Gửi bởi haichau97
trong 28-07-2012 - 12:19
 Gửi bởi haichau97
trong 27-07-2012 - 15:52
Gửi bởi haichau97
trong 27-07-2012 - 15:52
 Gửi bởi haichau97
trong 27-07-2012 - 14:56
Gửi bởi haichau97
trong 27-07-2012 - 14:56
 Gửi bởi haichau97
trong 26-07-2012 - 15:15
Gửi bởi haichau97
trong 26-07-2012 - 15:15
 Gửi bởi haichau97
trong 22-07-2012 - 22:29
Gửi bởi haichau97
trong 22-07-2012 - 22:29
:hì ,mình nhầm $\Leftrightarrow 3a^{4}+1\geq 4\begin{vmatrix} a^{3} \end{vmatrix}\geq 4a^{3}$ (luôn đúng vì nếu $a<0 VT>0;VP<0$ ,nếu $a$ dương hiển nhiên đúng ^^)Lỡ a<0 thì sao $\sqrt[4]{x^{12}}= x^{3}$ được hả bạn?
 Gửi bởi haichau97
trong 19-07-2012 - 22:15
Gửi bởi haichau97
trong 19-07-2012 - 22:15
 Gửi bởi haichau97
trong 19-07-2012 - 09:14
Gửi bởi haichau97
trong 19-07-2012 - 09:14
 Gửi bởi haichau97
trong 12-07-2012 - 16:48
Gửi bởi haichau97
trong 12-07-2012 - 16:48
 Gửi bởi haichau97
trong 10-07-2012 - 08:53
Gửi bởi haichau97
trong 10-07-2012 - 08:53
:hì ,ảnh mình có trong topic này rồi ,trang 19 , 2 bức cuối cùngBạn post ảnh bạn được k?Thích xem ảnh bạn hơn

 Gửi bởi haichau97
trong 09-07-2012 - 20:43
Gửi bởi haichau97
trong 09-07-2012 - 20:43
 Gửi bởi haichau97
trong 28-06-2012 - 21:25
Gửi bởi haichau97
trong 28-06-2012 - 21:25
 Gửi bởi haichau97
trong 28-06-2012 - 21:01
Gửi bởi haichau97
trong 28-06-2012 - 21:01
 Gửi bởi haichau97
trong 18-06-2012 - 15:11
Gửi bởi haichau97
trong 18-06-2012 - 15:11
Thấy chú Quân hãm lắm !
Mũi to, môi dày, không biết giống thể loại gì !!!
:haahhaha ,hình ông quân đây ư ,chắc giống thể loài thời nguyên thủy của loài người Việt hầy ,heheheThấy chú Quân hãm lắm !
Mũi to, môi dày, không biết giống thể loại gì !!!
 Gửi bởi haichau97
trong 16-06-2012 - 20:41
Gửi bởi haichau97
trong 16-06-2012 - 20:41

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học

 Tìm kiếm
Tìm kiếm