- etucgnaohtn và Rias Gremory thích
CaptainAmerica
Thống kê
- Nhóm: Thành viên
- Bài viết: 64
- Lượt xem: 4397
- Danh hiệu: Hạ sĩ
- Tuổi: 27 tuổi
- Ngày sinh: Tháng tư 10, 1997
-
Giới tính
 Không khai báo
Không khai báo
-
Đến từ
THPT Chuyên Nguyễn Bỉnh Khiêm
-
Sở thích
Ma \m/
Công cụ người dùng
Lần ghé thăm cuối
#377449 Con người có thể đọc và làm toán trong tình trạng vô thức
 Gửi bởi CaptainAmerica
trong 14-12-2012 - 00:19
Gửi bởi CaptainAmerica
trong 14-12-2012 - 00:19
#362963 Tính tỉ số khoảng cách từ $M$ đến $AB$; $AC$....
 Gửi bởi CaptainAmerica
trong 19-10-2012 - 11:17
Gửi bởi CaptainAmerica
trong 19-10-2012 - 11:17
Cho $\Delta ABC$ trung tuyến $AM$, phân giác $AD$ và $AN$ đối xứng $AM$ qua $AD$ ( $N \in BC$ ). Tính các tỉ số:
a) khoảng cách từ $M$ đến $AB$; $AC$.b) $\frac{NB}{NC}$
- BoFaKe yêu thích
#341890 Dựng ngũ giác đều nội tiếp đường tròn
 Gửi bởi CaptainAmerica
trong 30-07-2012 - 14:51
Gửi bởi CaptainAmerica
trong 30-07-2012 - 14:51
- hamdvk yêu thích
#327887 Cho tam giác ABC ngoại tiếp đường tròn (O)
 Gửi bởi CaptainAmerica
trong 22-06-2012 - 10:44
Gửi bởi CaptainAmerica
trong 22-06-2012 - 10:44
 Lời giải:
Lời giải:a)$\Delta MOB = \Delta NOB$ ( c.g.c )
$\Rightarrow ON=OM$
Mà $O$ $\in$ pg $\widehat{CBA}$
$\Rightarrow ON \perp BN;OM\perp BC$
$\Rightarrow BM; BN$ là các tiếp tuyến của (O)
$\Rightarrow$ N,M $\in (O)$
Tượg tự ta suy ra đpcm
b) Nhờ câu a ta cm dễ dàng $ANOP$ nội tiếp đtròn đk AO
Câu c bạn xem lại coi có sai đề ko nhé!
Vì $\Delta ABC$ cô định nên chỉ dựng được 1 đ.tròn nội tiếp nên 3 điểm nằm trên đtròn cũng phải cố định! Nó không thể chạy đc.. Khiến thức về cực trị hình học mình hơi kém nên có gì sai sót bạn chỉnh sửa dùm
- perfectstrong và akaipro thích
#327072 Tìm nghiệm nguyên dương của pt: $x!+y!=(x+y)!$
 Gửi bởi CaptainAmerica
trong 19-06-2012 - 20:39
Gửi bởi CaptainAmerica
trong 19-06-2012 - 20:39
(ký hiệu x! là tích các số tự nhiên từ 1 đến x....)
- ahead325 yêu thích
#323277 Làm sao để tự học toán THCS?
 Gửi bởi CaptainAmerica
trong 07-06-2012 - 23:43
Gửi bởi CaptainAmerica
trong 07-06-2012 - 23:43
- L Lawliet yêu thích
#323268 "Điều khác biệt giữa con trai và con gái sau khi chia tay"
 Gửi bởi CaptainAmerica
trong 07-06-2012 - 23:27
Gửi bởi CaptainAmerica
trong 07-06-2012 - 23:27
- chuot nhoc yêu thích
#323216 ĐỀ THI TUYỂN SINH VÀO TRƯỜNG TRUNG HỌC PHỔ THÔNG CHUYÊN ĐHSPHN 2012 V2
 Gửi bởi CaptainAmerica
trong 07-06-2012 - 20:12
Gửi bởi CaptainAmerica
trong 07-06-2012 - 20:12
Tớ làm hơi tắt nhéCâu 5 (3đ):
Cho hình vuông ABCD nội tiếp đường tròn $\left ( O \right )$. Điểm M thuộc cung nhỏ CD của $\left ( O \right )$, M khác C và D. MA cắt DB, DC theo thứ tự tại X ,Z ; MB cắt CA, CD tại Y,T; CX cắt DY tại K.
a, CMR : $\widehat{MXT}=\widehat{TXC}$, $\widehat{MYZ}=\widehat{ZYD}$ và $\widehat{CKD}=135^\circ$.
b, CMR :$\frac{KX}{MX}+\frac{KY}{MY}+\frac{ZT}{CD} =1$.
C, Gọi I là giao điểm của MK và CD. CMR : XT, YZ, OI cùng đi qua tâm đường tròn ngoại tiếp tam giác KZT.
--------------------------------------Hết------------------------------------
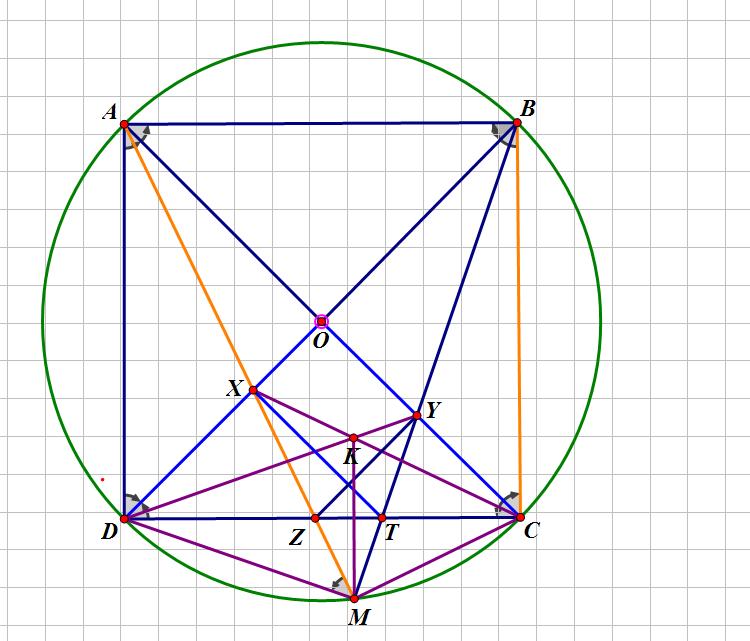
Ta có: $\widehat{AMB}=\widehat{BDC}=45^{\circ}$ ( Cùng chắn các cung có sđ = $90^{\circ}$
$\Rightarrow DXTM$ nt
$\Rightarrow \widehat{CDM}=\widehat{TXM}$
và $\widehat{TXD}=90^{\circ}$
Ta cm được $XTCB$ nt
$\Rightarrow \widehat{CBT}=\widehat{CXT}$
Mà $\widehat{CDM}=\widehat{CBM}$ ( cùng chắn cung )
Suy ra: $\widehat{TXM}=\widehat{TXC}$
Chứng minh tương tự ta được $\widehat{MYZ}=\widehat{ZYD}$
Chứng minh được: $K$ và $M$ đối xưng nhau qua BC ( 2 $\Delta$ Cân 2 bên ấy )
$\Rightarrow \widehat{DMC}=\widehat{DKC}$
Mà $\widehat{DMC}=135^{\circ}$ (chắn $\frac{3}{4}$ đường tròn )
$\Rightarrow$ đpcm @@
Câu b tí nữa ăn cơm xong làm
------------------------------------------------------------------------------------------
A có người làm dùm rồi! Khỏe quá
- perfectstrong và L Lawliet thích
#322483 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 21:30
Gửi bởi CaptainAmerica
trong 04-06-2012 - 21:30
Định lý:
Cho $\Delta ABC$ nội tiếp $(O,R)$. Gọi $x,y,z$ lần lượt là khoảng cách từ $O$ đến $BC,AC,AB$. Gọi $r$ là bán kính đường tròn nội tiếp $\Delta ABC$. Ta có:
a)Nếu$\Delta ABC$ nhọn thì công thức Carnot là $x+y+z=R+r$.
b)Nếu $\widehat{A}> 90^{\circ}$ thì công thức carno là $y+z-x=R+r$
Chứng minh:
a)Nếu $\Delta ABC$ nhọn
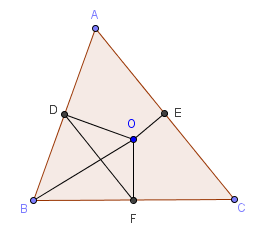
Gọi $F, E, D$ lần lượt là trung điểm của $BC,CA,AB$. Như vậy ta có
$OF=x, OE=y, OD=z$. Đặt$BC=a, AC=b, AB=c$.
Áp đụng bất đẳng thức Ptolemy cho tứ giác nội tiếp $OFBD$ ta có:
$OB.DF=OF.BD+FB.OD$hay $R.\frac{b}{2}=z.\frac{a}{2}+x.\frac{c}{2}$
Tương tự ta có $R.\frac{c}{2}=y.\frac{a}{2}+x.\frac{b}{2}$và $R.\frac{a}{2}=y.\frac{c}{2}+z.\frac{b}{2}$
ta lại có $r(\frac{b}{2}+\frac{a}{2}+\frac{c}{2})=S_{ABC}=S_{OBC}+S_{AOC}+S_{ABO}=x.\frac{a}{2}+y.\frac{b}{2}+z.\frac{c}{2}$
Cộng bốn biểu thức trên lại ta có
$(r+R)(\frac{a+b+c}{2})=(x+y+z)(\frac{a+b+c}{2})\Rightarrow$ đpcm.
b)Nếu $\widehat{A}> 90^{\circ}$ chứng minh tương tự.
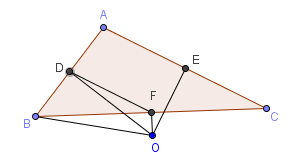
Viết dưới dạng lượng giác, công thức Carnot chính là hệ thức $cos A+cosB+cosC=1+\frac{r}{R}$. Chú ý hệ thức này đúng với mọi tam giác.
- HyunRi, CaptainCuong và Tea Coffee thích
#322344 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 11:00
Gửi bởi CaptainAmerica
trong 04-06-2012 - 11:00
Định lí: Cho $\Delta ABC$ và ba điểm $M,N,P$ lần lượt nằm trên $BC,CA,AB$. Khi đó các đường tròn ngoại tiếp các $\Delta$ APN,BPM và CMN đồng quy.
Chứng minh:

Gọi $S$ là giao điểm của $(BPM)$ và $(CMN)$.Ta sẽ chứng minh S nằm trên $(APN)$.
Thật vậy:
$(SN,SP)\equiv (SN,SM)+(SM,SP)\equiv (CN,CM)+(BM,BP)\equiv (CA,CB)+(BC,BA )\equiv (CA,BA)\equiv (AN,AP)(mod\pi )$
$\Rightarrow$ đpcm.
- Mylovemath, HyunRi, CaptainCuong và 1 người khác yêu thích
#322341 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:54
Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:54
Định lý:
Cho lục giác $ABCDEF$ ngoại tiếp $(O)$. Chứng minh rằng ba đường chéo lớn $AD, BE, CF$ đồng quy.
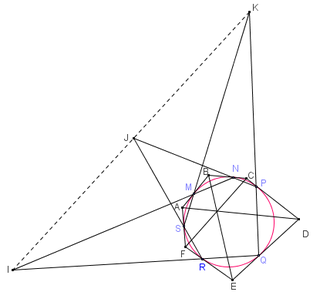
Chứng minh:
Ta kí hiệu các tiếp điểm của $(O)$ trên $AB,BC,CD,DE,EF,FA$ lần lượt là $M,N,P,Q,R,S$. Xét cực và đối cực đối với $(O)$. Gọi $K,I,J$ lần lượt là giao điểm của các cặp đường thẳng $(SM,PQ)$ ,$(MN,QR)$,$(NP,RS)$. Vì $SM$ và $PQ$ là đường đối cực của $A$ và $D$ nên $AD$ là đường đối cực của $K$. Tương tự $BE$ và $FC$ lần lượt là đường đối cực của $I$ và $J$.
Dùng định lí Pascal cho lục giác nội tiếp $MNPQRS$ ta có $I,J,K$ thẳng hàng. Nên ta có các đường đối cực của $I,J,K$ (lần lượt là $BE,CF,AD$) cùng đi qua cực của đường thẳng này (đường thẳng đi qua $I,J,K$) nên $AD,BE,CF$ đồng quy (đpcm).
Tương tự ngược lại có thế chứng minh định lí pascal thông qua Brianchon và cực đối cực
- HyunRi, CaptainCuong và Tea Coffee thích
#322336 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:45
Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:45
Định lý:
Cho 6 điểm $A,B,C,D,E,F$ cùng thuộc một đường tròn. Khi đó các giao điểm của các cặp cạnh $AB$ và $DE$, $BC$ và $EF$, $CD$ và $FA$ thẳng hàng.
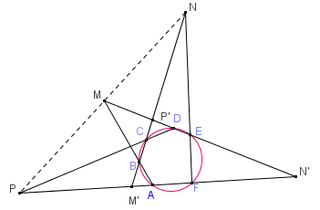
Chứng minh:
Gọi $P,M,N$ lần lượt là giao điểm của $AF$ và $CD$, $AB$ và $DE$, $BC$ và $EF$. Gọi $P', M', N'$ lần lượt là giao điểm của $BC$ và $DE$, $BC$ và $AF$, $DE$ và $AF$.
Áp dụng định lí Menelaus cho $\Delta P'M'N'$ với cát tuyến $PCD$:
$\frac{CP'}{CM'}.\frac{DN'}{DP'}.\frac{PM'}{PN'}=1$
$\Leftrightarrow \frac{PM'}{PN'}=\frac{CM'}{CP'}.\frac{DP'}{DN'}$
Tương tự ta có:
$\frac{NP'}{NM'}=\frac{FN'}{FM'}.\frac{EP'}{EN'}$và$\frac{MN'}{MP'}=\frac{AN'}{AM'}.\frac{BM'}{BP'}$
Nhân các biểu thức trên lại kết hợp với các biểu thức phương tích sau:
$BM'.CM'=AM'.FM'$
$EN'.DN'=FN'.AN'$
$CP'.BP'=DP'.EP'$
Ta có :
$\frac{NP'}{NM'}.\frac{MN'}{MP'}.\frac{PM'}{PN'}=1$
Áp dụng định lí Menelaus đảo ta có đpcm.
- macdangdung, HyunRi, CaptainCuong và 1 người khác yêu thích
#322327 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:39
Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:39
Định lý:
Cho tứ giác $ABCD$. Khi đó có $AC.BD \leq AB.CD + AD.BC$
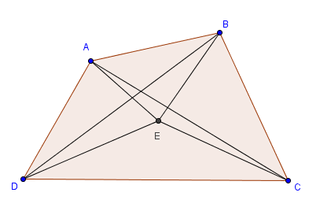
Chứng minh:
Lấy $E$ nằm trong tứ giác $ABCD$ sao cho
$\widehat{EDC}=\widehat{ADB}$và $\widehat{ECD}=\widehat{ABD}$
Khi đó$\Delta ABD \sim \Delta ECD \Rightarrow \frac{AB}{BD}=\frac{EC}{DC} \Leftrightarrow AB.DC=EC.BD$
Hơn nữa $\Delta ADE \sim \Delta BDC (c.g.c) \Rightarrow \frac{AD}{AE}=\frac{BD}{BC} \Leftrightarrow AD.CB=BD.AE$
Vậy $\Rightarrow AB.CD+BC.AD=BD(EA+EC)\geq BD.AC$(đpcm).
- HyunRi, CaptainCuong và Tea Coffee thích
#322322 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:33
Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:33
Định lí Với tứ giác nội tiếp $ABCD$ thì:
$AB.CD+AD.BC=AC.BD$
Chứng minh:

Lấy điểm $E$ thuộc $AC$ sao cho $\widehat{DEC}=\widehat{ADB}$
$\Rightarrow \Delta ADB \sim \Delta DEC$
$\Rightarrow \frac{AD}{DE}=\frac{BD}{DC}=\frac{AB}{EC}$
Tương tự $\Delta ADE\sim \Delta BDC \Rightarrow AE.BD=AD.BC$$\Rightarrow AD.BC+AB.CD=BD(EA+EC)=BD.AC$ (đpcm
- HyunRi, KimAnh126, CaptainCuong và 1 người khác yêu thích
#322318 Một số định lý và khái niệm hình học mang tên các nhà Toán học
 Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:25
Gửi bởi CaptainAmerica
trong 04-06-2012 - 10:25
Ở phần này tớ chỉ dùng hình xạ ảnh để dẫn dắt đến kết quả còn nội dung định lí và cách chứng minh thì hoàn toàn phù hợp với kiến thức hình THCS!
Ta có kết quả sau liên quan đến hình xạ ảnh: Các đường thẳng song song với nhau thì gặp nhau tại một điểm ở vô cực và ngược lại .
Vận dụng vào định lí Pappus ở trên , cho các điểm $A,B,C$ ra vô cực thì theo kết quả về hình xạ ảnh ta có
$YM//ZN$ ( Vì $YM,ZN$ cùng đi qua một điểm $(A)$ ở vô cực )Tương tự thì :$XN//YP$,$XM//ZP$.
Và khi ấy $M,N,P$ vẫn thẳng hàng. Ta phát biểu lại được một định lí đơn giản và hữu dụng sau đây:
Định lí:Trên mặt phẳng cho ba điểm $X,Y,Z$ thẳng hàng và ba điểm $M,N,P$ thỏa mãn XN//YP,YM//ZN,XM//ZP.
Khi đó ta cũng có M,N,P thẳng hàng.
Chứng minh:

Trường hợp $MP//XYZ$ thì đơn giản,bạn đọc tự chứng minh.
Ta sẽ xét khi $MP$ không song song với $XYZ$.
Gọi $S$ là giao điểm của $MP$ với $XYZ$.
Đường thẳng qua $X$ song song với $YP$ cắt $MP$ ở $N'$. Bài toán sẽ được gải quyết nếu ta chứng minh được rằng $ZN' // YM$ (Vì khi ấy $N'\equiv N$.
Thật vậy,chú ý $YP//XN'$, $ZP//XM$ nên theo Thales ta có:
$\frac{SY}{SZ}=\frac{SY}{SX}.\frac{SX}{SZ}=\frac{SP}{SN'}.\frac{SM}{SP}=\frac{SM}{SN'}$
Đến đây theo Thales đảo ta suy ra $ZN' //YM$.
$\Rightarrow$ đpcm
- N H Tu prince, CaptainCuong và Tea Coffee thích
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Likes: CaptainAmerica


 Tìm kiếm
Tìm kiếm










