pcfamily

Chọn hai đoạn thẳng có độ dài bất kỳ từ 0m đến 1m. Tính xác suất sao cho tỷ số độ dài của hai đoạn thẳng đó nằm trong khoảng $(\frac{1}{2},2)$.

Cho $ab+bc+ca=abc$. Chứng minh rằng:
$\frac{a}{a+bc}+\frac{b}{b+ca}+\frac{c}{c+ab}\leq \frac{a+b+c}{4}$

Bài này của Mỹ $2004$, hình như là $+3$ chứ không phải $+2$

Đúng rồi ạ, đề đúng thì em làm được rồi

Cho $a,b,c$ dương và $a+b+c=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$. Chứng minh rằng:

 

$\sum  \sqrt{a^2+3}\leq 2(a+b+c)$

Cho $a,b,c>0;a+b+c=1$. Chứng minh rằng:

 

$\sum \sqrt{\frac{a^3}{a^3+(1-a)^3}}\geq 1$

cho a,b,c >0 . CM:

$\sum \frac{a}{b+c}\geq \sum \frac{ a}{ a+b}$

* Bổ đề: BĐT hoán vị:

 Cho 2 dãy số thực $a_{1}\geq a_{2}\geq a_{1}$ và $b_{1}\geq b_{2}\geq b_{3}$

Ta có bđt: $a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}\geq a_{1}b_{i_{1}}+a_{2}b_{i_{2}}+a_{3}b_{i_{3}}$

Với $b_{i_{1}},b_{i_{2}},b_{i_{3}}$ là các hoán vị tuỳ ý của $b_{1},b_{2},b_{3}$

Chứng minh: $VT-VP=a_{1}(b_{1}-b_{i_{1}})+a_{2}(b_{2}-b_{i_{2}})+a_{3}(b_{3}-b_{i_{3}})$

$=(a_{1}-a_{2})(b_{1}-b_{i_1})+(a_{2}-a_{3})(b_{1}+b_{2}-b_{i_1}-b_{i_{2}})+a_{3}(b_{1}+b_{2}+b_{3}-b_{i_{1}}-b_{i_{2}}-b_{i_{3}})$

$\geq 0\Rightarrow DPCM$

Trở lại bài toán:

Không mất tính tổng quát, giả sử $a\geq b\geq c$

nên $\frac{1}{b+c}\geq \frac{1}{c+a}\geq \frac{1}{a+b}$

Áp dụng BĐT hoán vị có ĐPCM

 

 

 

Xét $\frac{x}{y}-\frac{z(x+y)}{y(y+z)}=\frac{xy+xz-xz-zy}{y(y+z)}=\frac{x-z}{y+z}$

Tương tự, bđt tương đương:

$\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\geq \frac{z}{y+z}+\frac{x}{z+x}+\frac{y}{x+y}$

Không mất tính tổng quát, giả sử $x\geq y\geq z$

 nên $\frac{1}{y+z}\geq \frac{1}{z+x}\geq \frac{1}{x+y}$

Áp dụng bất đẳng thức hoán vị có ĐPCM.

Cho a,b,c dương thỏa mãn ab+ac+bc=3,  $a\geq c$ tìm giá trị nhỏ nhất của 

P= $\frac{1}{\left ( a+1 \right )^{2}}+\frac{2}{\left ( 1+b \right )^{2}}+\frac{3}{\left ( 1+c \right )^{2}}$

$a\geq c\Rightarrow \frac{1}{(c+1)^2}\geq \frac{1}{(a+1)^2}$

$\Rightarrow P\geq \frac{2}{(1+a)^2}+\frac{2}{(1+b)^2}+\frac{2}{(1+c)^2}$

Áp dụng bđt: $\frac{1}{(a+1)^{2}}+\frac{1}{(b+1)^{2}}\geq \frac{1}{1+ab}$

Tương tự, cộng lại được:

$P\geq \frac{1}{1+ab}+\frac{1}{1+bc}+\frac{1}{1+ca}\geq \frac{9}{ab+bc+ca+3}=\frac{3}{2}$

Đẳng thức xảy ra tại $a=b=c=1$

Cho $\Delta ABC,BC=a,CA=b,AB=c$ và $M$ là điểm nằm trong tam giác. Gọi $H,I,K$ là hình chiếu của $M$ lên $BC,CA,AB$

a) CMR: $\frac{a}{MH}\overrightarrow{MH}+\frac{b}{MI}\overrightarrow{MI}+\frac{c}{MK}\overrightarrow{MK}=\overrightarrow{0}$

b) CMR $M$ là trọng tâm $\Delta HIK$ khi và chỉ khi $a^2\overrightarrow{MA}+b^2\overrightarrow{MB}+c^2\overrightarrow{MC}=\overrightarrow{0}$

Câu a/ là trường hợp riêng của định lý con nhím. Bạn xem thêm ở đây 

 

b/ Với mọi điểm $M$ trong tam giác $ABC$ ta có:

Mượn anh Perfectstrong cái hình

 

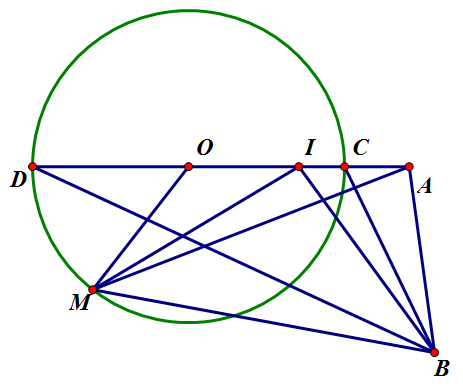
Vẽ đường thẳng $OA$ giao $(O)$ tại $C,D$ và $C$ nằm giữa $O,A$
Trên đoạn $OC$ lấy $I$ sao cho $R={\sqrt 2}OI \Rightarrow \dfrac{OI}{OM}=\dfrac{1}{\sqrt 2}=\dfrac{OM}{OA}$           
 $\Rightarrow \vartriangle OMI \sim \vartriangle OAM (c.g.c) \Rightarrow MA=\sqrt 2 MI$
$\Rightarrow MA+\sqrt 2 MB=\sqrt 2(MI+MB) \geq \sqrt 2 IB$
Dấu bằng xảy ra khi $M=IB\bigcap (O)$

Vậy $Min(MA+\sqrt{2}MB)=IB \Leftrightarrow M=IB\bigcap (O)$

 

P/s: Bạn này chắc ở Phú Xuyên thi sáng nay hở

Bất đẳng thức đã mở hàng

 

b) Cho x,y,z $\geq$ 0; x+y+z=1.

CMR : 4(1-a)(1-b)(1-c)$\leq$ a+b+2c

Đã có ở đây: http://diendantoanho...lant41-a1-b1-c/

Hệ này không phải hệ đẳng cấp, mình cũng có theo dõi màn cãi nhau của hai bạn nhưng không tiện xen vào

Mình có một thắc mắc muốn thỉnh giáo 

VD1.1.9 trang 9, quyển "Sáng tạo bất đẳng thức" của anh PKH như thế này:

Cho các số thực a,b,c thỏa mãn $a^2+b^2+c^2=3$. Chứng minh bất đẳng thức sau:

$|a|+|b|+|c|-abc\leq4$

 

LỜI GIẢI: Áp dụng trực tiếp bđt AM-GM:

$a^2b^2c^2\leq (\frac{a^2+b^2+c^2}{3})^3=1\Rightarrow -abc\leq 1$

$(|a|+|b|+|c|)^2\leq 3(a^2+b^2+c^2)=9\Rightarrow |a|+|b|+|c|\leq 3$

Cộng lại ta được ĐPCM. Sau đó tác giả có một nhận xét ở dưới:

" Bạn đọc thử làm bài toán trên nếu ta bỏ đi các đấu giá trị tuyệt đối, tìm max của $a+b+c-abc$. Đây là một bài toán rất thú vị và không dễ. "

 

Rất tò mò với dòng nhận xét này, mình đang không hiểu vì sao khi bỏ dấu GTTĐ đi bài toán lại thay đổi, bạn nào có lời giải thì làm ơn đăng lên cho mình và mọi người tham khảo. Thân