$\left\{\begin{matrix} \frac{1}{3x}+\frac{2x}{3y} = (x+\sqrt{y})/(2x^2+y) & \\ 2x(1+y)=(2+\sqrt{y})(\sqrt{2x+1}) & \end{matrix}\right.$
- leduylinh1998 yêu thích
 Nam
Nam
 Gửi bởi 899225
trong 12-12-2014 - 22:07
Gửi bởi 899225
trong 12-12-2014 - 22:07
$\left\{\begin{matrix} \frac{1}{3x}+\frac{2x}{3y} = (x+\sqrt{y})/(2x^2+y) & \\ 2x(1+y)=(2+\sqrt{y})(\sqrt{2x+1}) & \end{matrix}\right.$
 Gửi bởi 899225
trong 17-09-2014 - 16:23
Gửi bởi 899225
trong 17-09-2014 - 16:23
Lâu lâu vô chém phát:
BĐT<=>$+\frac{1}{1+\frac{z}{y}}+\frac{1}{1+\frac{x}{z}}$ (1)
Dễ thấy $\frac{z}{y}*\frac{x}{z}\geq 1$ vì $x\geq y$
Nhớ đến BĐT:$\frac{1}{1+a^2}+\frac{1}{1+b^2}\geq \frac{2}{1+ab}$ vs ab=1
=>(1)$\geq \frac{1}{2+\frac{3y}{x}}+\frac{2}{1+\frac{x}{y}}$
Đăt x/y=t; 1=<t<=4 => (1)$\geq \frac{2}{1+t}+\frac{t}{2t+3}$
Từ đây đạo hàm => (1)$\geq \frac{33}{34}$
(Chỗ đạo hàm hơi oải )
 Gửi bởi 899225
trong 08-03-2013 - 21:11
Gửi bởi 899225
trong 08-03-2013 - 21:11
 Gửi bởi 899225
trong 23-09-2012 - 20:25
Gửi bởi 899225
trong 23-09-2012 - 20:25

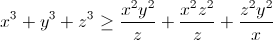

 Gửi bởi 899225
trong 23-09-2012 - 18:35
Gửi bởi 899225
trong 23-09-2012 - 18:35
 Gửi bởi 899225
trong 22-09-2012 - 23:37
Gửi bởi 899225
trong 22-09-2012 - 23:37
 Gửi bởi 899225
trong 22-09-2012 - 23:33
Gửi bởi 899225
trong 22-09-2012 - 23:33
 Gửi bởi 899225
trong 14-09-2012 - 15:59
Gửi bởi 899225
trong 14-09-2012 - 15:59
 Gửi bởi 899225
trong 14-09-2012 - 13:45
Gửi bởi 899225
trong 14-09-2012 - 13:45
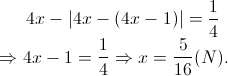
 Gửi bởi 899225
trong 13-09-2012 - 21:06
Gửi bởi 899225
trong 13-09-2012 - 21:06
 Gửi bởi 899225
trong 13-09-2012 - 20:08
Gửi bởi 899225
trong 13-09-2012 - 20:08
 Gửi bởi 899225
trong 11-09-2012 - 23:26
Gửi bởi 899225
trong 11-09-2012 - 23:26

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học

 Tìm kiếm
Tìm kiếm