Primary

phải đề OLP 30 tháng 4 ko vậy bạn

Đúng vậy, thấy bài này tính hay hay post lên
Cái này không cần dùng tích phân cũng được

Cho a, b, c là 3 cạnh của tam giác. Chứng minh rằng:$$\sum \frac{\sqrt{b+c-a}}{\sqrt{b}+\sqrt{c}-\sqrt{a}}\leq 3$$

Giải:

$\frac{x^2-x-6}{(x^2-9)(x+1)}\leq 0$

$\Leftrightarrow \frac{(x-3)(x+2)}{(x-3)(x+3)(x+1)}\leq 0$ (1)

$x-3=0 \Leftrightarrow x=3$
$x+2=0 \Leftrightarrow x=-2$
$x-3=0 \Leftrightarrow x=3$
$x+3=0 \Leftrightarrow x=-3$
$x+1=0 \Leftrightarrow x=-1$

Bảng xét dấu:
.............
..............


Cho em hỏi tại sao ở chỗ (1) ta không triệt tiêu cái (x-3) luôn vậy?

Nhưng em nghĩ là dù x lớn hơn hay nhỏ hơn 3 thì trên chia dưới cũng bằng 1 thôi. Không hiểu thiệt.

Vì ta chưa biết $x>3$ hay không. Mình nghĩ thế ^^. Không biết đúng không!

Vấn đề thực chất là x=3 thì đa VP vô nghĩa
Nên có thể triệt tiêu sau khi xét x khác 3

Bài toán: Cho đường tròn $\left ( O;2,5 \right )$. Chứng minh rằng trong $10$ điểm nằm bên trong đường tròn thì tồn tại $2$ điểm có khoảng cách nhỏ hơn $2$.

Em chỉ biết thế này:
Gọi $d(X_i,X_{i+1})$ là khoảng cách giữa 2 điểm $X_i,X_{i+1}$
Chu vi đường tròn $C=2.2,5\pi =5\pi$ $\Rightarrow$ khoảng cách trung bình giữa 2 điểm $X_i,X_{i+1}$ là $d(X_i,X_{i+1})=\frac{\pi }{2}<2$
Nếu khoảng cách giữa 2 điểm $X_i,X_{i+1}$ là $d(X_i,X_{i+1})$>2 suy ra có ít nhất 2 điểm trong 10 điểm có khoảng cách $d(X_k,X_{k+1})$<2 với $k\neq i$
Do đó ta có điều phải chứng minh.

Mình xin góp 1 bài:
Bài 8: Tìm GTNN của $\sum (\frac{a}{b-c})^2$, với $a\neq b\neq c$

Bài toán 7: Cho $x, y, z \geq 0$, tìm min của $P$ thỏa mãn:
$$P=(\sum_{sym} {xy})(\sum_{sym} \frac{1}{x^2+y^2})$$

Theo bất đẳng thức Cauchy-Schwarz:
$P\geq (\sum xy)(\sum \frac{1}{2(x+y)^2})\Leftrightarrow 2P\geq (xy+yz+zx)[\frac{1}{(x+y)^2}+\frac{1}{(y+z)^2}+\frac{1}{(z+x)^2}]$
Vế phải chính là bất đẳng thức Iran năm 1996: https://phudinhgioihan.wordpress.com/
Đến đây $2P\geq \frac{9}{4}\Leftrightarrow P\geq \frac{9}{8}$
Dấu "=" xảy ra $\Leftrightarrow x=y=z>0$

Thế $x=-1$ thì sao?Max $t=3$ mà.?

Mình cũng không rõ nữa cứ thế giá trị x =-1 hoặc x=2 vào là được vì x thuộc [-1;2], cái này thầy cô không ai dạy hết

• Giải phương trình nghiệm nguyên dương: .

Biểu diễn liên phân số của là:
,
biểu diễn này có chu kì r=1 lẻ, do đó nghiệm của phương trình là 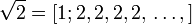() với n có dạng , các giản phân ở vị trí lẻ.
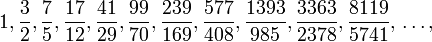Dãy giản phân của : . Chú ý dãy số trên được bắt đầu với số thứ tự bằng 0.
Lấy các phân số ở vị trí lẻ ta được nghiệm nguyên dương của phương trình là: (3,2) (17,12), (99,70), (577,408), (3363,2378), ... và tất nhiên cả nghiệm tầm thường là (1,0).
Đây là phương trình Pell như bạn nói

Gọi các chiều cao tương ứng tỉ lệ với $3:4:5$ là $h_1;h_2;h_3$
Ta có:$\dfrac{h_1}{3}=\dfrac{h_2}{4}=\dfrac{h_3}{5}$
Gọi các cạnh tương ứng với các đường cao là $a,b,c$,vá giả sử tỉ lệ theo$x:y:z$
Ta có $\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}$
Nhân về theo vế,ta được:
$\dfrac{ah_1}{3x}=\dfrac{bh_2}{4x}=\dfrac{ch_1}{5x}$
Vì $ah_1=bh_2=ch_3$(cùng bằng $2S_{\Delta}$)
Như vậy thì $3x=4y=5z$
Để $x:y:z$ tối giản thì $3x=4y=5z=LCM(3;4;5)=60$
Từ đây suy ra $x:y:z=20:15:12$

Hình như $h_a+h_b,h_b+h_c,h_c+h_a$ tỉ lệ với 3,4,5 thì phải

Cho hàm số: y = x⁴ + 2mx² + 9
Tìm m để hàm số cắt trục hoành tại 4 điểm phân biệt

Đặt $t=x^2,t\geq 0$$\Rightarrow y=t^2+2mt+9$
Hàm số y cắt trục hoành tại 4 điểm phân biệt $\Leftrightarrow t^2+2mt+9=0$ có 2 nghiệm dương phân biệt $\Leftrightarrow \Delta '=m^2-36> 0\Leftrightarrow m> 6\vee m< -6$

Bài toán [Tham Lang]
Cho các số thực $a,b,c,d$. Tìm GTNN của biểu thức :
$$P=(a-b+1)^2+(b-4)^2+(2c-d+7)^2+(d+3)^2+(a-4b+3c-6d+9)^2$$

Em có cách này:
$$P=(a-b+1)^2+(b-4)^2+(2c-d+7)^2+(d+3)^2+(a-4b+3c-6d+10-1)^2$$$\geq (-1)^2\Leftrightarrow P\geq 1$
$\Rightarrow MinP=1$ khi $a=3;b=4;c=-5;d=-3$
Hình như bài toán này không mang đến 1 lời giải đẹp

Tìm các giá trị của tham số $m$ sao cho hệ phương trình sau có nghiệm:
$$\left\{\begin{matrix} x^2+3xz+z^2=1 (1)\\ 3y^2+3yz+z^2=4 (2) \\ x^2-xy+y^2=m (3)\end{matrix}\right.$$

Xét x=y=z=0 không phải là nghiệm của hệ
*Nếu x=0 hệ trở thành $\left\{\begin{matrix}z^2=1 & & \\ 3y^2+3yz+z^2=4 & & \\ y^2=m & & \end{matrix}\right.$ $\Rightarrow m=\frac{3\pm \sqrt{5}}{2}$
*Nếu y=0 hệ trở thành $\left\{\begin{matrix}x^2+3xz+z^2=1 & & & \\ z^2=4 & & & \\ x^2=m & & & \end{matrix}\right.$ $\Rightarrow m=15\pm 6\sqrt{6}$
*Nếu z=0 hệ trở thành $\left\{\begin{matrix}x^2=1 & & & \\ 3y^2=4 & & & \\ x^2-xy+y^2=m & & & \end{matrix}\right.$ $\Rightarrow m=\frac{7\pm 2\sqrt{3}}{4}$
*Nếu x,y,z khác 0
Đặt $x=ay,x=bz\Rightarrow x=ay=bz$ $(a,b\neq 0)$
$\Rightarrow y=\frac{bz}{a},x^2=axy$ hay $y^2=\frac{b^2z^2}{a^2},xy=\frac{x^2}{a}$
$(1)\Leftrightarrow bz^2+3bz.\frac{bz}{a}+z^2=1\Leftrightarrow z^2=\frac{a}{ab^2+a+3b^2}$
$\Rightarrow y^2=\frac{b^2}{a(ab^2+a+3b^2)},x^2=\frac{a^2b^2}{ab^2+a+3b^2}$
$(2)\Leftrightarrow \frac{3b^2}{a(ab^2+a+3b^2)}+\frac{3b.a}{a(ab^2+a+3b^2)}+\frac{a}{ab^2+a+3b^2}=4$ $\Leftrightarrow 3b^2+3ab-4a^2b^2-12ab^2-3a^2=0$ (*)
Ta có $(1)\Leftrightarrow \frac{a^2b^2}{ab^2+a+3b^2}+\frac{a}{ab62+a+3b^2}+\frac{3ab^2}{ab^2+a+3b^2}=1\Leftrightarrow (ab^2-b^2)(a+3)=0\Leftrightarrow a=1\vee a=-3,(b\neq 0)$
Với a=1 thay vào (*) ta được $-13b^2+3b-3=0$ (Vô nghiệm)
Với a=-3 thay vào (*) ta được $b^2-3b-9=0\Leftrightarrow b=\frac{3\pm 3\sqrt{5}}{2}$
Khi đó $x=-3y$ và thay vào (1) ta được $z^2=1\Leftrightarrow z=\pm 1$
Nếu $b=\frac{3+3\sqrt{5}}{2}$ thì:
* z=1$\Rightarrow y=-\frac{1+\sqrt{5}}{2}\Rightarrow x=\frac{3+3\sqrt{5}}{2}$
$(3)\Leftrightarrow m=\frac{39+13\sqrt{5}}{2}$
* z=-1$\Rightarrow y=\frac{1+\sqrt{5}}{2}\Rightarrow x=-\frac{3+3\sqrt{5}}{2}$
$(3)\Leftrightarrow m=\frac{39+13\sqrt{5}}{2}$
Nếu $b=\frac{3-3\sqrt{5}}{2}$ thì
* z=1 $\Rightarrow y=\frac{-1+\sqrt{5}}{2}\Rightarrow x=\frac{3-3\sqrt{5}}{2}$
$(3)\Leftrightarrow \frac{39-13\sqrt{5}}{2}$
* z=-1 $\Rightarrow y=\frac{1-\sqrt{5}}{2}\Rightarrow x=\frac{-3+3\sqrt{5}}{2}$
$(3)\Leftrightarrow m=\frac{39-13\sqrt{5}}{2}$
Thử lại m thỏa yêu cầu bài toán
Vậy $m\in \left \{ \frac{39\pm 13\sqrt{5}}{2};\frac{3\pm \sqrt{5}}{2};15\pm 6\sqrt{6};\frac{7\pm 2\sqrt{3}}{4} \right \}$ thì hệ có nghiệm

Thầy thanh nói đúng đó, cái này hiển nhiên là sai khi ta chọn khéo phần lẻ của $x$
$x=[x]+\{x\}$
Nên $[nx]=[n[x]+n\{x\}]=n[x]+[n\{x\}]$
Đến đây lựa chọn cẩn thận ta sẽ chọn được $\{x\}\geq \dfrac{2}{n}$ (với $n\geq 3$) mà vẫn đảm bảo được $\{x\}<1$ khi ấy $[n\{x\}]\geq 2$ nên BDT của bạn đã bị sai

Lúc đầu nhìn vào thử mọi số thấy đúng nhưng chứng minh không được và thử như nguyenta98 thì kết quả lại sai. Vậy chẳng lẽ chỉ có duy nhất 1 cách hay sao ???

Chứng minh với mọi số $a,b,c \in \mathbb{R^{+}}$,ta luôn có:
$\dfrac{x}{y+2z}+\dfrac{y}{z+2x}+\dfrac{z}{x+2y} \ge 1$
________
Không khó đâu

Theo bất đẳng thức Cauchy-Schwarz
$\sum \frac{x}{y+2z}=\sum \frac{x^2}{xy+2xz}\geq \frac{(x+y+z)^2}{3(xy+yz+xz)}\geq \frac{(x+y+z)^2}{3(x^2+y^2+z^2)}\geq 1$ ??

@: Primary
Em chứng minh cái "dễ thấy" này đi.
$n\lfloor x\rfloor\le\lfloor nx\rfloor\le n\lfloor x\rfloor+1,\;\forall n\in\mathbb N^*$

*Với mọi số thực x, y thì:
$[x+y]=[[x]+[y]+\left \{ x \right \}+\left \{ y \right \}]=[x]+[y]+[\left \{ x \right \}+\left \{ y \right \}]$
Vì $0\leq \left \{ x \right \},\left \{ y \right \}<1$ nên
$\Rightarrow [x]+[y]\leq [x+y]\leq [x+y]+1$ (*)
1) Chứng minh: $n[x]\leq [nx]$
Áp dụng (*) ta có : $n[x]=[x]+...+[x]\leq [x+x]+[x]+...+[x]\leq ...\leq [x+...+x]=n[x]\Leftrightarrow n[x]\leq [nx]$
Do đó (1) được chứng minh
2) Chứng minh $[nx]\leq n[x]+1$
*Nếu $n=2k, k\in \mathbb{N}$:
$[nx]=[kx+kx]\leq [kx]+[kx]+1=2[kx]+1\leq [2kx]+1\Leftrightarrow [nx]\leq n[x]+1$
*Nếu $n=2k+1,k\in \mathbb{N}$: (phần này cứng như đá)