nhatquangsin

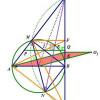
Cho tam giác $ABC$ nội tiếp $\left ( O \right )$. Đường cao $BE,CF$ cắt nhau tại $H$. $EF$ cắt $AH$ tại $M$. Gọi $I$ là tâm đường tròn ngoại tiếp $AEHF$. CMR: $CM \perp BI$

 

@mod: lần sau nhớ gõ latex nhé

Áp dụng định lý Brokard cho tứ giác AEHF nội tiếp ta có đpcm

Ta có thể xét không mất tính tổng quát các số $x,y,z$ là số tự nhiên.

Ta có $a^2\equiv 0;1(mod\ 4)$. Là $1$ nếu $a$ lẻ, và là $0$ nếu $a$ chẵn

Nếu cả $x,y$ là số lẻ thì khi đó $a^2+b^2+c^2\equiv 2;3 (mod\ 4)$ và $x^2y^2\equiv 1 (mod\ 4)$ (vô lý).

Nếu trong hai số $x,y$ có một số lẻ và một số chẵn thì $x^2+y^2+z^2\equiv 1;2 (mod\ 4)$ và $x^2y^2\equiv 0 (mod\ 4)$ (vô lý)

Từ đó suy ra cả $x,y$ đều chẵn, nên $z$ chẵn.

Đặt $x=2x_1;y=2y_1;z=2z_1$ ta có phương trình $x_1^2+y_1^2+z_1^2=4x_1^2y_1^2$

Lập luận tương tự thì ta cũng có $z_1;y_1;z_1$ là các số chẵn.

Lập lại quy trình như vậy thì ta sẽ có $x,y,z$ là các lũy thừa của $2$ với số mũ vô hạn, điều này vô lý.

Suy ra $z=y=x=0$

Cho $x=y=0$ ta được $2f(0)=[f(0)]^2\Leftrightarrow \begin{bmatrix} f(0)=0\\ f(0)=2 \end{bmatrix}$

Xét trường hợp $f(0)=0$. Cho $x=0$ ta được $f(-y)=-f(y)$ với mọi $y\in \mathbb{R}$. Thay $y$ bằng $-y$ ta có: $f(x+y)-f(xy)=f(x)+f(y)-f(x)f(y),\forall x,y\in \mathbb{R}$.

Từ đó ta có $f(x+y)+f(x-y)=2f(x),\forall x,y\in \mathbb{R}$. Cho $x=y$ ta có $f(2x)=2f(x),\forall x\in \mathbb{R}$. Do đó $f(x+y)+f(x-y)=f(2x),\forall x,y\in \mathbb{R}$.

Đặt $u=x+y,y=x-y$ ta có $f(u)+f(v)=f(u+v),\forall u,v\in \mathbb{R}$. Hay $f(x)+f(y)=f(x+y),\forall x,y\in \mathbb{R}$.$\rightarrow f(x)=ax,\forall x\in \mathbb{R}$, $a$ là một hằng số.

Mà ta cũng có $f(xy)=f(x).f(y),\forall x,y\in \mathbb{R}$. Từ đó suy ra $\begin{bmatrix} f(x)\equiv 0\\ f(x)=x,\forall x\in \mathbb{R} \end{bmatrix}$.

Thử lại thỏa mãn.

Xét trường hợp $f(0)=2$. Cho $x=0$ ta có $f(y)=f(-y),\forall y\in \mathbb{R}$.

Thay $y=-y$ ta có $f(x+y)+f(xy)=f(x)-f(y)+f(x)f(y),\forall x,y\in \mathbb{R}$

Do đó suy ra $f(x+y)=f(x-y),\forall x,y\in \mathbb{R}$. Chọn $x=y=\frac{u}{2}$ thì ta có $f(u)=2,\forall u\in \mathbb{R}$. Hay $f(x)=2,\forall x\in \mathbb{R}$. Thế lại thỏa mãn.

Vậy các hàm thỏa mãn là $f(x)\equiv 0;f(x)\equiv 2;f(x)\equiv x$.

Em xin bổ sung một chút bài làm:

Ta xây dựng $70$ thành phố có đường đến $A$, $70$ thành phố có đường từ $A$ đến và xây dựng các đỉnh còn lại tương tự $A$. Ngoài ra ở mỗi thành phố trong $70$ có đường từ $A$ đến thì ta cũng xây dựng các đường đến $70$ thành phố có đường đến $A$ với mỗi một đỉnh như vậy.

Xét đồ thì $210$ đỉnh.

Gọi $A$ là thành phố có nhiều đường đi nhất. Khi đó ta xét các trường hợp sau:

-Hai thành phố $B$ và $C$ có đường đi từ $A$ đến: không thể có đường giữa hai thành phố.$(1)$

-Hai thành phố $B$ và $C$ cùng có đường đến $A$: không thể có đường giữa hai thành phố.$(2)$

-Hai thành phố $B$ và $C$ có đường từ $A$ đến $B$ và từ $C$ đến $A$ thì có đường từ $B$ đến $C$ và không có đường ngược lại.

Đặt số thành phố có đường từ $A$ đến là $a$, số thành phố có đường đến $A$ là $b$, các thành phố không có đường đến $A$ cũng không có đường từ $A$ là $c$.

Khi đó ta có $a+b+c=209$.

Theo $(1)$ và $(2)$ thì các thành phố có đường từ $A$ đến và từ $A$ đi sẽ không có đường nối tới nhau. Xét đồ thị $210$ đỉnh thì $A$ là đỉnh có bậc cao nhất là $a+b$. Do đó số thành phố không liên quan đến $A$ phải có số đỉnh nhỏ hơn hoặc bằng $a+b$. Gọi $S_1$ là số đường đi của các thành phố này thì vì có $c$ thành phố như vậy nên $S_1\leq c(a+b)$.

Gọi $S_2$ là số đường tới $A$ thì $S_2=a+b$. Gọi $S_3$ là số đường giữa các thành phố còn lại thì vì trong $a$ thành phố có đường từ $A$ và $b$ thành phố có đường đến $A$ có thể có đường nối nhau nên số đường lớn nhất có thể là $ab$.

Vậy số đường đi là $S=S_1+S_2+S_3\leq ab+a+b+(a+b)c=ab+c(a+1)+c(b+1)\leq \frac{(a+b+c+1)^2}{3}=14700$

Dấu = xảy ra khi $a=b=c+1$ tức ta cần xây dựng $70$ thành phố có đường từ $A$ đến các đỉnh, $70$ thành phố có đường đến $A$ và các đỉnh còn lại xây dựng tương tự điểm $A$.