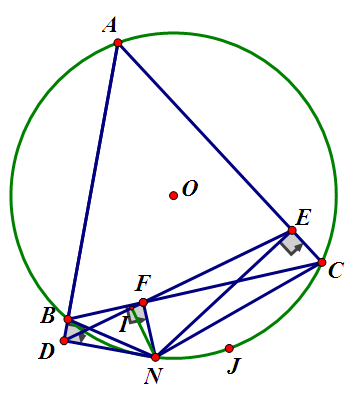
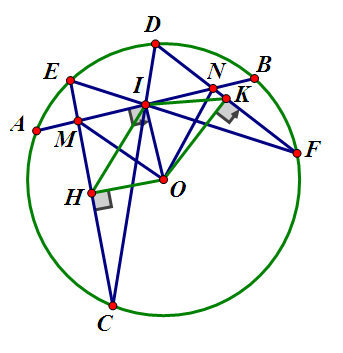
Từ N hạ $NF\bot BC$ tại F; $NI\bot DE$ tại $I$
$\Rightarrow D,I,F,E$ thẳng hàng
Dễ dàng chứng minh được $\widehat{NDF}=\widehat{NBF}$
$\widehat{NEF}=\widehat{NCF}$
$\Rightarrow \triangle NDE \sim \triangle NBC(g.g)$
$\Rightarrow \frac{DE}{MI}=\frac{BC}{MF}$
hay $\Rightarrow \frac{MF}{MI}=\frac{BC}{DE}\geq 1$
$\Rightarrow DE\leq BC$
Dấu = xảy ra $\Leftrightarrow N\equiv J$( AJ là đường kính của (O))


 Tìm kiếm
Tìm kiếm Nữ
Nữ