malx

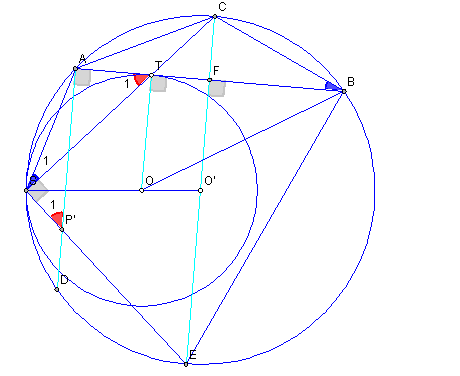
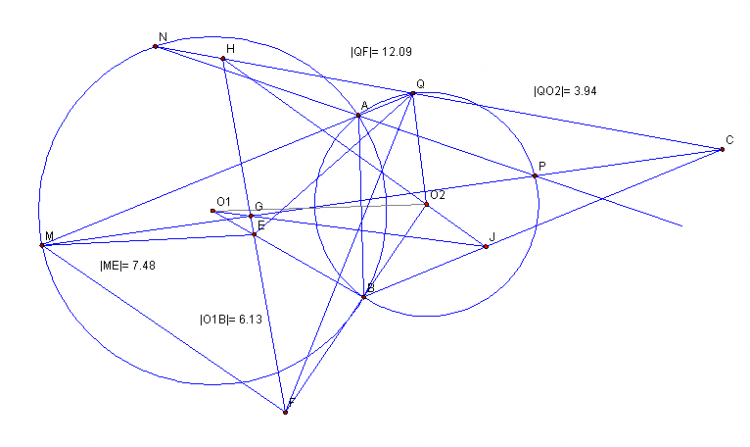
Ta sẽ đảo bài toán một chút như sau: Để $AT$ cắt $(O’)$ tại $C, CO’$ cắt lại đ.t. này tại $E$, đường thẳng qua $A$ vuông góc với $AB$ cắt $SE$ tại $P’$. Ta sẽ cm $P’, O, B$ thẳng hàng, như thế $P’\equiv P$ và ta có đ.p.c.m. Để cm điều này chỉ cần chỉ ra là $TO/AP’ = BT/BA$ (*). Gọi $r, R$ là bán kính $(O), (O’)$.

Trước hết dễ thấy $C$ là trung điểm cung nhỏ $AB$, cũng như $AC^{2} = CB^{2} = CT. CS$. Theo định lý sin trong $\Delta ATS$ có: $AP’/sin ASP’ = AP’ / cos S_{1} = AT/sin S_{1}$

Vì thế $AP’ = \frac{AS.cos S_{1}}{sin S_{1}}$ và như thế

$ \frac{TO}{AP’} = \frac{TO.tg S_{1}}{AT} = \frac{r.CF}{AT.FB}$

$= \frac{r.CF.2R}{AT.FB.2R} = \frac{r.CB^{2}}{2R.AT.FB} = \frac{ST.CB^{2}}{2SC.AT.FB} = \frac{ST.CT.CS}{2SC.AT.FB}$

$= \frac{ST.CT}{AT.AB} = \frac{AT.TB}{AT.AB} = \frac{TB}{AB}$

Đây chính là (*) và lời giải hoàn tất.

Ủng họ bạn #haitienbg#:

Bài 1, Hình bên phải

Gọi giao điểm của đt $(DEF)$ với $AD, BC$ là $H, G$. Dễ thấy $GH\parallel AC$. Do $\Delta ADE$ là tam giác cân nên $DE\parallel HF$, tương tự như thế có $EB\parallel GF$.

Trước hết thấy $\overarc{HF} = \overarc{HF}$ (nhỏ) $ =\overarc{BF}$ (nhỏ) nên $BF = FH$ hay $MF$ là trung trực của $BH$.

Lại có $\overarc{HGD} = \overarc{EBF} = \overarc{BDG}$, vì thế $\overarc{DEB} = \overarc{GF}$ (nhỏ) hay $GD\parallel BH$, $DGHB$ là hình thang cân nên các đường tréo $DH, BG$ và đường trung trực chung $MF$ của hai đáy đồng qui.

Bài 2, Hình bên trái

Dễ thấy $\angle F_{1} +\angle F_{2} = \angle C_{1} + \angle E_{1}$.

Vì $\angle FAS = \angle FDS$ và $\Delta ASB\sim\Delta DSC$ nên có $sin F_{1} / sin F_{2} = AS/DS = AB/DC = ED/DC = sin C_{1} / sin E_{1}$.

Do vậy có $F_{1} = C_{1}$ (đpcm), cũng như $F_{2} = E_{1}$

Một cách chứng minh khác cho Dao's circle:

Gọi $K, L, M$ là giao điểm của các đường trung trực của $AG, BG, CG$ (xem hình vẽ), tâm của các đường tròn được nói tới là $A_{1}, A_{2}, B_{1}, B_{2}, C_{1},C_{2}$. Do tứ giác $A’MC’G$ là tứ giác nội tiếp nên $\angle DGC’ = \angle A’MC’$ hay là $\angle AGE + \angle EGC = \angle MA_{2}C_{1} + \angle A_{2}C_{1}M$ (1)

Lưu ý là $\Delta GC’C_{1}\sim \Delta GA’A_{2}$ và vì $E$ là trung điểm của $AC$ nên

$sin AGE/sin EGC = GC/GA = GC’/GA’ = GC_{1}/GA_{2} = MC_{1}/MA_{2} = sin MA_{2}C_{1}/sin\angle A_{2}C_{1}M$ (2)

(1) và (2) cho $\angle AGE = \angle A_{2}C_{1}M$ nhưng dễ thấy $\angle AGE =\angle MKL$ nên tứ giác $KA_{2}C_{1}L$ là tứ giác nội tiếp, do $A_{1}C_{2}\parallel KL$ nên $A_{1}A_{2}C_{1}C_{2}$ là tứ giác nội tiếp.

Làm tương tự như trên hai lần nữa sẽ thấy sáu điểm $A_{1}, A_{2}, B_{1}, B_{2}, C_{1},C_{2}$ quả thực nằm trên một đường tròn.

Gọi $H$ là trực tâm của $\Delta ABC$ với các đường cao $AA’, BB’, CC’$, giao điểm của $(O)$ với đường tròn đường kính $AA_{1}$ với tâm $D$ là $G, GH$ cắt đường tròn $(D)$ tại $K$. Dễ thấy $A’$ nằm trên $(D)$, ta có $HG. HK = HA. HA’ = HB. HB’ = HC. HC’$ nên cả hai đường tròn còn lại, một đường kính $BB_{1}$ tâm $E$, một đường kính $CC_{1}$ tâm $F$, đều đi qua $G$ và $K$.

Tiếp theo, gọi $L$ là trung điểm của $GH$ và $M$ trung điểm $AH$, từ các điều ở trên ta có $HL. HK = HA’. HM$ hay bốn điểm $M, K, A’, L$ nằm trên một đường tròn. Làm tương tự như vậy ta sẽ thu được $K$ nằm trên đường tròn Euler (đi qua $A’, B’, C’, M, ….$)

Post nhầm bài, đề nghị admin xoá giúp.

Trước hết ta chứng minh bổ đề sau: nếu đường tròn đường kính $EF$ với tâm $I$ cắt $(O)$ tại $X, Y$ thì $IX, IY$ là các tiếp tuyến tới $(O)$ với bán kính $R$.

Gọi $H\equiv EF\cap BD, K\equiv AC\cap BD$. Lưu ý $FK$ là polar của $E$ và $EK$ là polar của $F$, vì thế $K$ là trực tâm của $\Delta OEF$ và $OK\perp EF$. Gọi $R$ là chân đường cao từ $F$ tới $OE$, hiển nhiên $R$ nằm trên $(I)$, lại do $FR$ là polar của $E$ nên $OR. OE = R^{2}= OY^{2}$ , điều này có nghĩa là $OY$ là tiếp tuyến tới $(I)$, đồng nghĩa với $IY$ là tiếp tuyến tới $(O)$, tương tự như vậy với $IX$.

Quay lại bài toán. Do $ON\perp BH$ và $OK\perp EF$, lại do $OMKN$ là tứ giác nội tiếp nên $\angle GHN = \angle NOK = \angle NMK$, tức là tứ giác $GHMN$ nội tiếp hay nói cách khác, đường tròn $(GNM)$ đi qua $H$. Lưu ý là ba điểm $M, N, I$ nằm trên đường thẳng Newton-Gauss. Vì $(E, F; G, H) = -1$ nên có $IN. IM = IG. IH = IF^{2}$, nhưng do bổ đề trên nên $IG. IH = IY^{2}$, điều này có nghĩa là $I$ nằm trên trục đẳng phương của $(GNMH)$ và $(O)$, tức $PQ$. Do đó ta có đpcm là $EF, PQ, MN$ đồng qui tại $I$.

_{Để chứng minh (N, D; B, C) = -1 chỉ cần làm như sau: Gọi BF và CG là các đường cao trong tam giác ABC, N' là giao của FG và BC. Vì N'G. N'F = N'B. N'C nên N' nằm trên trục đẳng phương của hai đường tròn (O) và (O1), nghĩa là N' nằm trên XY. Do đó N' trùng N và (N, D; B, C) = -1.}

Rảnh ngồi đọc bài của thầy. Em xin ủng hộ thầy một cách giải khác dùng pole-polar đối với đường tròn $(O)$.

Gọi $G\equiv CE\cap AD, H\equiv CB\cap AE, F\equiv CD\cap AE$. Quan sát tứ giác nội tiếp $CEDA$ thì $GF$ là polar của $P$, vì $PB$ là tiếp tuyến nên $B$ cũng nằm trên polar của $P$, vậy nên ba điểm $G, F, B$ thẳng hàng. Lưu ý là $PO$ là polar của $G$. Tiếp tục quan sát tứ giác nội tiếp $CEBA$ thì thấy điểm $H$ nằm trên polar của $G$. Vậy nên ba điểm $P, H, O$ thẳng hàng và ta có đpcm.

Việc chứng minh $CE$ là phân giác ngoài của $\angle BCA$ là đơn giản, làm như #barcavodich# là được. Để kết thúc bài toán chỉ cần chứng minh tiếp $AE$ là phân giác ngoài của $\angle BAC$, tức là phân giác $\angle CAX$ là đủ.

$YT$ cắt $(O_{1})$ tại điểm thứ hai $H, HA$ cắt $XY$ tại $K$. Dễ thấy $HS\parallel XY$ (so sánh góc qua tiếp tuyến trung của hai đường tròn tại $T$). Do $\angle TCE= \angle SHT = \angle TYE$ nên tứ giác $TEYC$ nội tiếp. Do $\angle TAK = \angle HST = \angle TXK$ nên tứ giác $AXKT$ nội tiếp. Do $\angle ACE = \angle SHA = \angle AKE$ nên tứ giác $AEKC$ nội tiếp.

Gọi $L$ là giao điểm của hai đường tròn $(AXKT)$ và $(TEYC)$. Vì $\angle ELT = \angle TYE = \angle AXT$ nên ba điểm $A, E, L$ thẳng hàng. Vì $\angle TLK = \angle TXK = \angle TYC$ nên ba điểm $L, K, C$ thẳng hàng (phải viết chi tiết vì sợ phép tương tự rồi J). Đến đây dễ thấy $\angle EAX = \angle EKL = \angle CKY = \angle CAE$ nên ta có đpcm: $AE$ là phân giác $\angle CAX$

Nhận xét: $CK$ là phân giác $\angle ACY$ nên có phỏng đoán là bài này có thể giải được bằng hình học cao cấp (spiral similarity, spiral symmetry ? ...). Rất tiếc là do lười chưa học mấy thứ này.

Ừa, thấy vấn đề rồi. Thế thì bài mock này cũng không hay lắm. Cơ bản là chứng duợc được là $HG\parallel O_{1}O_{2}$.

Sử dung bổ để: Trong tam giác $BLK$ với các đường cao $BR, LD, KI$, đường tròn đi qua $L, K$, cắt $BL, BK$ tại $O_{1}, O_{2}$, điểm $J$ di động trên đường cao $BR, JO_{1}$ cắt $KI$ tại $G, JO_{2}$ cắt $LD$ tại $H$ thì $HG\parallel ID\parallel O_{1}O_{2}$ (Xem hình vẽ thứ nhất)

Đề bài của bổ đề này còn dài hơn chứng minh,dùng Menelaus (chỉ cần 1 lần) là sẽ ra ngay.

Quay lại bài chính, việc chứng minh $LD, KI$ (với $D\equiv O_{2}B\cap NQ$ và $I\equiv O_{1}B\cap PM$) là các đường cao, cũng như chứng minh tứ giác $LKO_{2}O_{1}$ là tứ giác nội tiếp là đơn giản - xem hình vẽ thứ hai.

Hoàng ơi, sao lại cãi thầy, thầy bảo sai là phải sai mà lại, còn mốc với meo gì

Gợi ý: Bài này là tổng hợp của hai bài hình rất được biết tới:

1. Đường thẳng Éo le (Euler của tam giác $XYZ$ đi qua $O$. Có nhiều cách chứng minh tính chất này, ngoài các cách sử dung hình học cao cấp hơn có cả cách dùng hình học cơ bản, ngắn gọn

2. Đường $OI$ (với $O$ là tâm ngoại tiếp, $I$ là tâm nội tiếp $\Delta ABC \perp EF$. Cũng có cách chứng minh dùng hình học cơ bản, ngắn gọn.

Bài 5 Cho hai đường tròn (O₁), (O₂) tiếp xúc ngoài nhau tại M. A là điểm thuộc (O₂). AB, AC là tiếp tuyến của (O₁). MB, MC cắt (O₂) tại D, E khác M. Chứng minh DE đi qua trung điểm AB, AC.

Trước hết dễ thấy $CB\parallel DE$ (so sánh góc thông qua tiếp tuyến chung của hai đường tròn tại $M$). Qua $E$ kẻ đường $Ex\parallel AC$ thì có $\angle xEC = \angle ECA = \angle CBM = \angle MDE$ nên $Ex$ là tiếp tuyến của $(O_{2})$ tại $E$.

Giả sử $AM$ cắt $(O_{1})$ tại $F$. Nhận xét thấy tứ giác nội tiếp $FCMB$ có $M$ là giao điểm của $(O_{1})$ với $FA$ mà $A$ lại là giao điểm của hai tiếp tuyến tại $B, C$ nên tứ giác này là tứ giác điều hòa. Chùm điều hòa $M(MCFB)$ cắt $(O_{2})$ cho tứ giác $MEAD$ điều hòa. Chùm điều hòa $E(MADE)$ cắt $AC$ cho $(C, A; N, \infty) = -1$ với $N\equiv ED\cap AC$ nên $N$ phải là trung điểm của $AC$, $ED$ cũng đi qua trung điểm của $AB$.

Bài 4 Cho tam giác ABC đường tròn nội tiếp (I) tiếp xúc BC, CA, AB tại D, E, F.(K) là đường tròn thay đổi đi qua B, C sao cho EF cắt (K) tại P, Q. Chứng minh rằng đường tròn ngoại tiếp tam giác DPQ luôn đi qua điểm cố định khác D.

Gọi giao điểm của $EF$ và $BC$ là $H$. Ta có $(H, D; A, C) = -1$, nếu $M$ là trung điểm của $BC$ thì $M$ có các tính chất sau $MB^{2} = MC^{2} = MD. MH$ (*) , cũng như $HD.HM = HB. HC$ (**). Ta sẽ sử dụng tính chất (**) này.

Lưu ý $HB. HC = HP. HQ$ nên $HP.HQ = HD.HM$, tứ giác $PQMD$ là tứ giác nội tiếp, nói cách khác đường tròn ngoại tiếp $(DPQ)$ luôn đi qua trung điểm $M$ của $BC$.

Bài 1 của bạn tuy hơi nhầm một chút nhưng không sao, đây là một bài hình hay.

Gọi $Lx, Ly$ là phân giác các góc $\angle ALB$ và $\angle ALC$. Đường tròn ngoại tiếp $(ANB)$ cắt $BC$ tại $Q$ thì do $\angle AQB = \angle BNA = \angle yLC$ nên $AQ\parallel Ly$ và $AQ\perp Lx$, tam giác $ALQ$ là tam giác cân, $AQ = AL$

Tương tự như vậy, nếu đường tròn $(AMC)$ cắt $BC$ tại $P$ thì $PL = AL$.

Gọi $r$ là bán kính đường tròn $(O)$. $OC_{2} - OB_{2} = (OC^{2} - r^{2}) - (OB^{2} - r^{2}) = CA.CN - BA.BM = CB.CQ - BP.BC = BC (CQ - BP) = BC (CL + LQ - BL - LP) = BC (LC - LB) = LC^{2} - LB^{2}$.

$LO$ quả thực vuông góc với $BC$