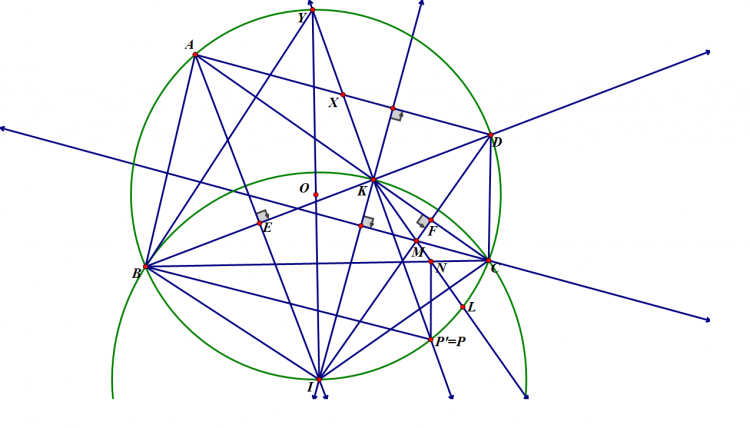
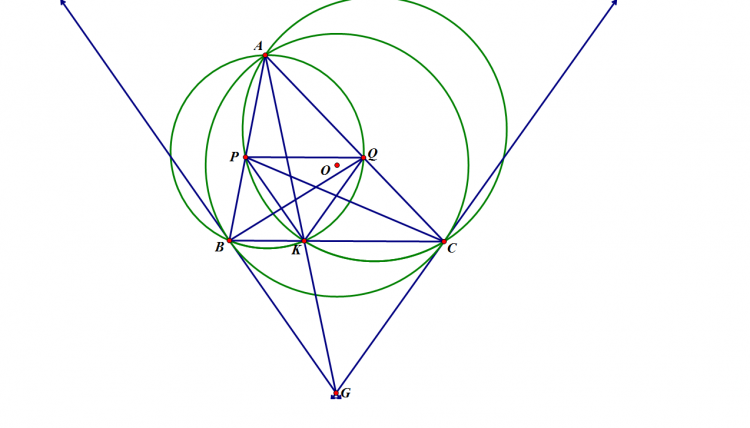
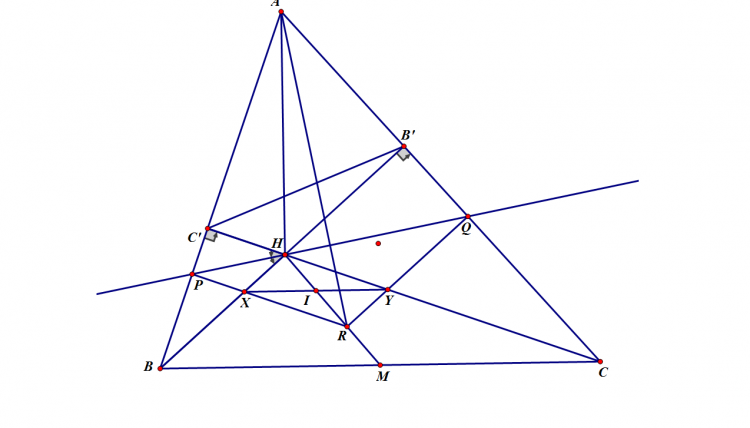
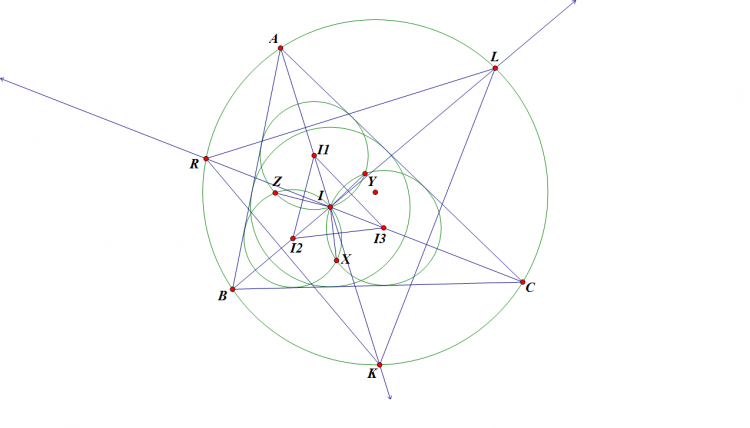
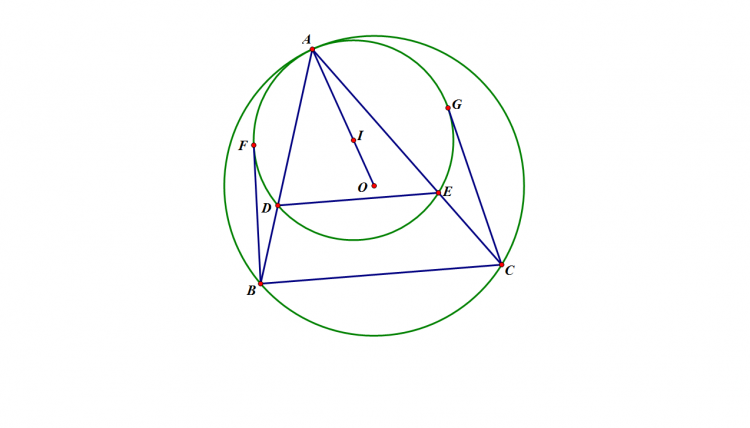
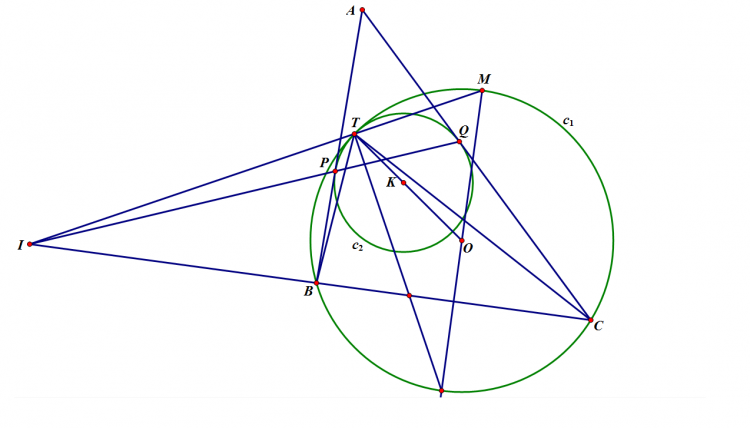
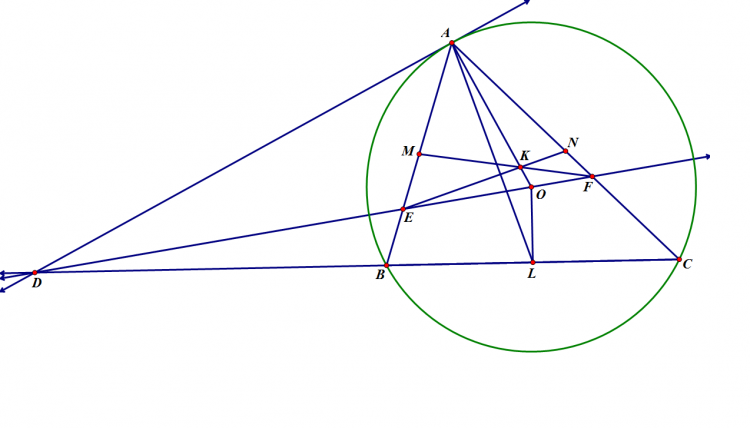
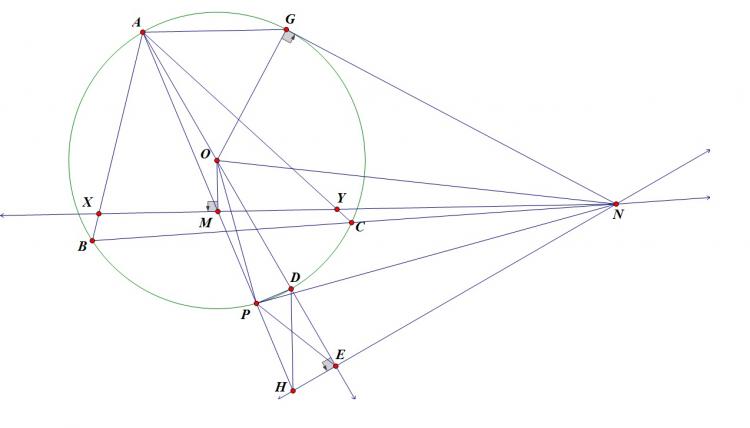
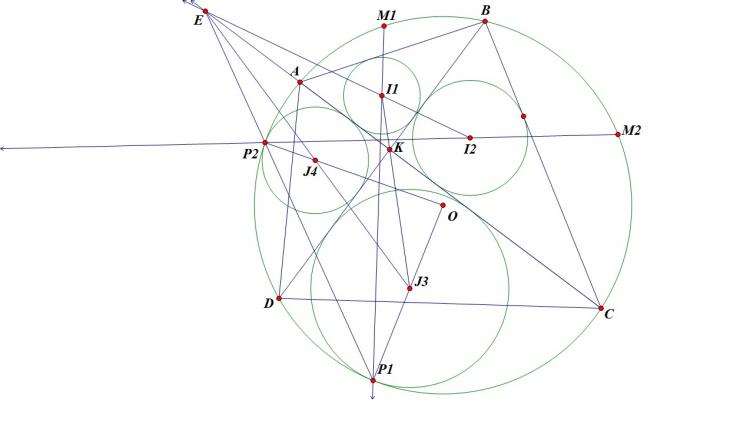
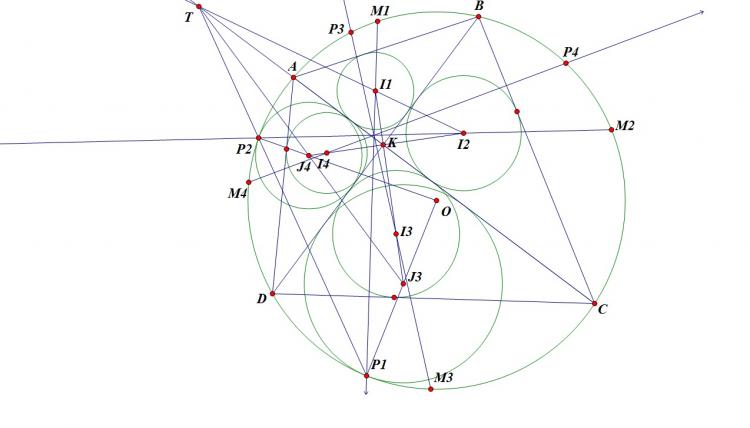
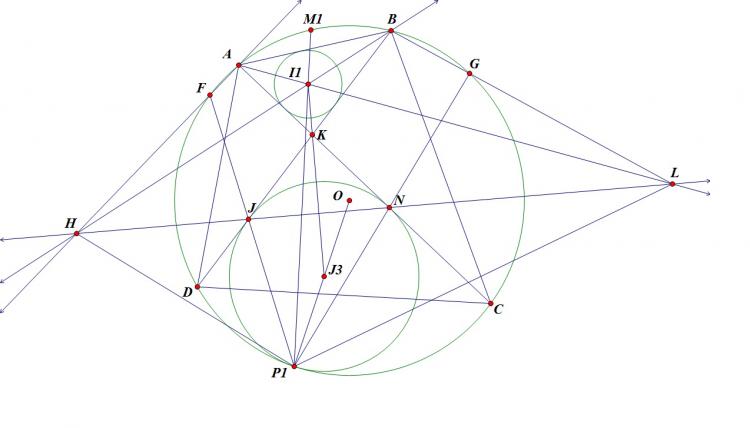
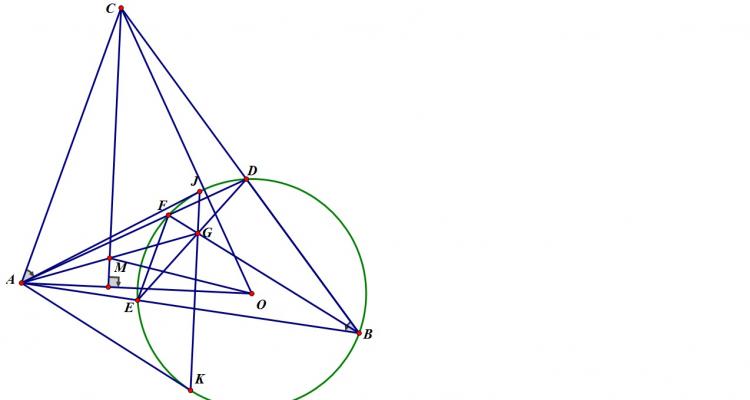
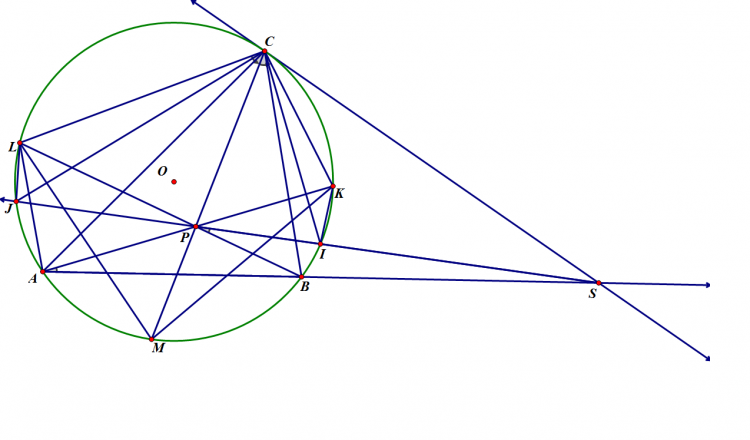
Cho tam giác $ABC$ nội tiếp $(O)$, phân giác trong góc $A$ cắt $(O)$ tại $D$. Một điểm $P$ di chuyển trên đoạn $AD$. $PB$ cắt $AC,(O)$ thứ tự tại $E,M$; $PC$ cắt $AB,(O)$ thứ tự tại $F,N$. $EF$ cắt $MN$ tại $G$; $NE, MF$ cắt nhau tại $L$; $DG$ cắt $(O)$ tại $S$. Chứng minh $SL$ đi qua 1 điểm cố định khi $P$ thay đổi.
- dogsteven yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam











 Gửi bởi
Gửi bởi