dkhanhht98

Tìm đa thức hệ số nguyên $P(x)$ sao cho với mọi số nguyên dương $n$ ta đều có $P(n)$ là ước của $2^n-1$.

Chém bài "dễ thương" nhất cái đã

Gọi $k$ là số các ô còn trống.

Giả sử $k \geq 33$

Ta cần CM trong một hàng (hoặc cột) không tồn tại 6 ô vuông trống

Giả sử tồn tại 6 ô vuông trống trên một hàng.

Khi đó trên mỗi cột có ít nhất 6 ô có quân cờ, suy ra $k \leq 28$, vô lí

Vậy trong một hàng (hoặc cột) có nhiều nhất 5 ô vuông trống

Vì $k \geq 33$ nên theo nguyên tắc Dirichlet tồn tại một hàng có 5 ô vuông trống.

Tương tự, tồn tại một cột có 5 ô vuông trống.

Hàng đó và cột đó giao nhau tại một ô, ô đó phải là ô có cờ

Gọi các hàng chứa 5 ô ở cột đó là $r_1,r_2,...,r_5$

Gọi các cột chứa 5 ô ở hàng đó là $c_1,c_2,...,c_5$

Dễ thấy có ít nhất $30$ ô chứa quân cờ

Gọi ô được giao bởi cột $i$ và hàng $j$ là $a_{ij}$ và ta biểu diễn $a_{ij}=1$ nếu ô $a_{ij}$ chứa quân cờ, ngược lại $a_{ij}=0$

Nhận xét: có nhiều nhất một $a_{ij}=0$ (nếu có 2 $a_{ij}=0$ thì $k \leq 32$, mâu thuẫn)

Vậy có ít nhất một cột trong $8$ cột không chứa bất kì quân cờ nào trong $30$ quân cờ trên.

Vì số ô chưa đặt quân cờ này không vượt quá $5$ nên ta có ít nhất 3 ô có quân cờ.

Suy ra có ít nhất $33$ ô vuông có quân cờ, mâu thuẫn

Suy ra đpcm

Nhờ bạn nói rõ chỗ này!

cho biểu thức P(x) = $\sqrt{x^{8}+12x+12} - 3x$ . x₁, x₂ là nghiệm của phương trình $x^{2}-x-1=0$

CMR : P(x₁) = P(x₂)

Ta sẽ dùng đẳng thức $x_1^2-x_1-1=0$ để biến đổi "hạ bậc" $x^8+12x+12$.

Ta có $x_1^2-x_1-1=0 \Rightarrow x_1^4=x_1^2+2x_1+1=(x_1^2-x_1)+3x_1+1\Rightarrow x_1^4 =3x_1+2 \Rightarrow x_1^8+12x_1+12=(3x_1+2)^2+12x_1+12=(3x_1+4)^2$.

Cho $\Delta ABC$. Chứng minh rằng:

 

$1+\frac{r}{R}=cosA+cosB+cosC$

Có cách này biến đổi về cạnh:

Ta có $r=\dfrac{S}{p}$, $R=\dfrac{abc}{4S}$

$\Rightarrow 1+\dfrac{r}{R}=1+\dfrac{4S^2}{pabc}=1+\dfrac{(b+c-a(c+a-b)(a+b-c)}{2abc}=\dfrac{-a^3-b^3-c^3+ab(a+b)+bc(b+c)+ca(c+a)}{2abc}$.

Lại có

cos$A$+cos$B$+cos$C$=$\dfrac{a(b^2+c^2-a^2)+b(c^2+a^2-b^2)+c(a^2+b^2-c^2)}{2abc}$.

Từ đó dễ có $1+\frac{r}{R}$=cos$A$+cos$B$+cos$C$.

Hình vẽ

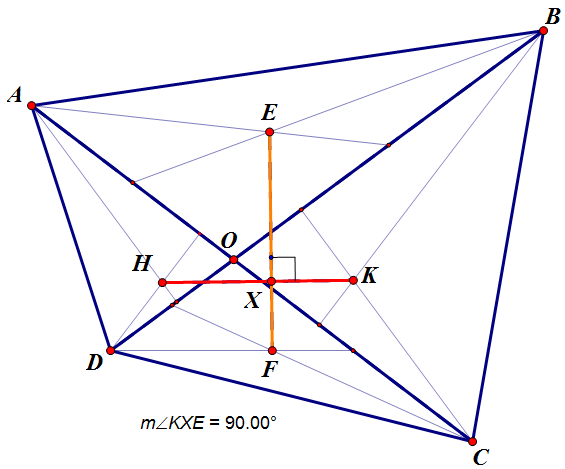
Ta sẽ đi chứng minh $\overrightarrow{EF}.\overrightarrow{HK}=0.(1)$

Thật vậy, ta có

$(1) \Leftrightarrow (\overrightarrow{AD}+\overrightarrow{BC})(\overrightarrow{OH}-\overrightarrow{OK})=0$

$\Leftrightarrow \overrightarrow{OH}.\overrightarrow{BC}=\overrightarrow{OK}.\overrightarrow{AD}$

(điều này đúng do cos($\overrightarrow{OH}, \overrightarrow{BC}$)=cos($\overrightarrow{OK}, \overrightarrow{AD}$))

(cặp góc có cạnh tương ứng vuông góc

và $OH.BC=OK.AD$ (chú ý $\dfrac{OH}{AD}= cot \widehat{AOD}$).

Chứng minh hoặc phản biện mềnh đề:

    ''Tồn tại vô số số nguyên tố $p$ thỏa mãn $2p+1$ là số nguyên tố''.

Đây là phần lý thuyết của bài thuyết trình. Các ví dụ minh họa và bài tập sẽ được tiếp tục update. Hẹn mọi người vào sáng mai.

Nhờ thầy tải lên dùm em một số bài tập phần này.

Bài 1: 

a) Tìm số tự nhiên n (n>0) sao cho tổng: 1! + 2! + 3! + ... + n! là một số chính phương.

Xét các trường hợp $n$ bằng $1$, $2$, $3$. Với $n\ge 4$ thì tổng đó có tận cùng là $3$ nên không là số chính phương.

Chú ý $n!$ có tận cùng là $0$ với $n\ge 4$.

Hình vẽ.

Dùng phương pháp hàm số giải quyết bài toán này.

Tính đạo hàm của hàm P ta được : P' = $\frac{-2a^{2}+4a+2 }{\left ( 2a^{2}+2a \right )^2}$

P'=0 có hai nghiệm là a= 1-$\sqrt{2}$ và a = 1+ $\sqrt{2}$

Vẽ bảng biến thiên ta xác định được maxP = P(1 + $\sqrt{2}$) = $\frac{1}{4\sqrt{2}+6}$

Không cần phải phức tạp vậy đâu.

Đặt $a-1=t$. Khi đó $P=\dfrac{t}{6t+2(t^2+2)}$

Áp dụng Bất đẳng thức AM-GM ta có $t^2+2\ge 2\sqrt{2}t\Rightarrow 6t+2(t^2+2)\ge t(6+4\sqrt{2})$.

Suy ra $P \ge \dfrac{1}{6+4\sqrt{2}}$.

Dấu bằng xảy ra khi $a=1+\sqrt{2}$.

chứng minh $(\sqrt{3}+ \sqrt{2})^{2008} + (\sqrt{3}- \sqrt{2})^{2008}$ là số tự nhiên. Tìm chữ số cuối

Có cách này không dùng quy nạp:

Xét $x_1=(\sqrt{3}+\sqrt{2})^2$ và $x_2=(\sqrt{3}-\sqrt{2})^2$.

Ta có $x_1+x_2=10$ và $x_1x_2=1$.

Xét $S_n=x_1^n+x_2^n$, thì có $S_1=10, S_2=98, S_3=970, S_4=9602$

Chứng minh được $S_{n+2}=10S_{n+1}-S_n$.

Khi đó dễ có

     1. $S_n$ là số tự nhiên $\forall n\Rightarrow S_{1004}$ là số tự nhiên hay $(\sqrt{3}+ \sqrt{2})^{2008} + (\sqrt{3}-\sqrt{2})^{2008}$  là số tự nhiên.

        2.  $S_n\equiv -S_{n-2}\equiv S_{n-4}$ (mod$10$) $\Rightarrow S_{4k}\equiv S_4$(mod$10$)

           $\Rightarrow S_{1004}\equiv S_4\equiv 9602\equiv 2$(mod$10$).

$\boxed{3}$ Cho tam giác nhọn $ABC$, $AD$ là đường cao từ $A$ hạ xuống $BC$. Đường thẳng $l$ đi qua $D$ song song $AB$, $t$ là tiếp tuyến đường tròn ngoại tiếp $ABC$ tại $A$. Gọi $E$ là giao điểm của $l$ và $t$.  Chứng minh $CE$ vuông góc với $t$.

Câu 3 hình không khó:

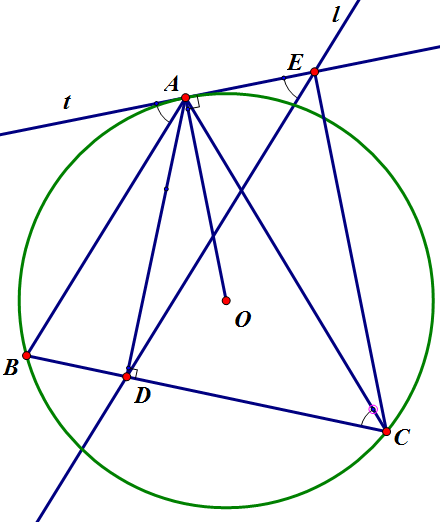
Ta có $\widehat{BAt}=\widehat{AED}=\widehat{ACB}\Rightarrow$ tứ giác AECD nội tiếp

         $\Rightarrow\widehat{CEA}=\widehat{ADC}=90^o\Rightarrow CE\perp t$

Một cách giải khác nữa: (Sử dụng phương pháp hàm số bậc nhất)

    Giả sử $a\ge b\ge c$. Khi đó $c\le1$.

    Viết lại $VT=ab(c-2)+c^2+(3-c)^2$ với $ab\le\dfrac{(3-c)^2}{4}, c-2<0$

                $\Rightarrow VT\ge (c-2)\dfrac{(3-c)^2}{4}+c^2+(3-c)^2$

    Ta sẽ chứng minh  $(c-2)\dfrac{(3-c)^2}{4}+c^2+(3-c)^2\ge4 (1)$.

    Thật vậy:

              (1)$\Leftrightarrow(c-1)^2(c+2)\ge0$,đúng do $c\ge0$.