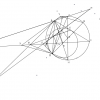
Mở rộng. Cho tam giác $ABC$ nội tiếp $(O)$ với $B, C$ cố định và $A$ di chuyển. Một đường tròn cố định đi qua $BC$ và cắt $AC, AB$ tại $E, F$. Một điểm $O$ cố định nằm trên trung trực $BC$. Lấy $H$ thuộc $BE$, $K$ thuộc $CF$ thỏa mãn $OH || AC, OK || AB$. Khi đó trung trực $HK$ đi qua một điểm cố định.
dogsteven
Thống kê
- Nhóm: Thành viên
- Bài viết: 1567
- Lượt xem: 15459
- Danh hiệu: Đại úy
- Tuổi: 24 tuổi
- Ngày sinh: Tháng hai 18, 2000
-
Giới tính
 Nam
Nam
-
Đến từ
Chuyên toán Trần Hưng Đạo, Bình Thuận
-
Sở thích
Anti số học.
Công cụ người dùng
Lần ghé thăm cuối
Trong chủ đề: Trung trực $HK$ đi qua điểm cố định
25-12-2017 - 00:02
Trong chủ đề: ĐỀ THI OLYMPIC TOÁN TRƯỜNG ĐÔNG TOÁN PHỔ THÔNG KHU VỰC BẮC TRUNG BỘ NĂM 2017
06-12-2017 - 19:23
Bổ đề này chứng minh thế nào anh? Nó đã xuất hiện ở những bài toán nào ? Sách nào ?
Bổ đề này là một định phần để chứng minh định lý về cực và đối cực: Cho đường tròn $(O)$ và ba điểm $A, B, C$ phân biệt. Khi đó $A, B, C$ thẳng hàng khi và chỉ khi đối cực của $A, B, C$ đồng quy hoặc đôi một song song.
Chứng minh.
Gọi $M, N$ là trung điểm $CD, EF$, khi đó $OM.OA = R^2 = ON.OB$ nên $MNBA$ nội tiếp.
Từ đó $\angle GOM= 90^o-\angle OGM = 90^o-\angle ONM = 90^o-\angle OAB$ nên $OG\perp AB$ và dễ có $OG.OH=OM.OA=R^2$
Trở lại bài toán, ta dựng tương tự $BC$, tiếp tuyến tại $A$ của $(ABC)$ cắt $EF$ tại $W$ thì $W, K, L$ thẳng hàng do trục đẳng phương của đường tròn Euler và $(ABC)$. Kẻ tiếp tuyến khác $WA$ đến $(O)$ là $WV'$
Từ đó áp dụng bổ đề ra suy ra $BS, CT, AV'$ đồng quy tại điểm $G$ thỏa $OG=\dfrac{R^2}{d(O, KL)}$ nên ta có $V\equiv V'$
Trong chủ đề: ĐỀ THI OLYMPIC TOÁN TRƯỜNG ĐÔNG TOÁN PHỔ THÔNG KHU VỰC BẮC TRUNG BỘ NĂM 2017
06-12-2017 - 11:24
Bài 6.
a. Dùng hai kết quả sau:
1. Cho tam giác $ABC$ với $M, N$ thuộc $BC$. Khi đó $(AMN)$ tiếp xúc với $(ABC)$ khi và chỉ khi $\angle MAN$ và $\angle BAC$ có chung phân giác.
2. Cho tam giác $ABC$, phân giác $AD$, $T$ thuộc $BC$. Khi đó $AT=TD$ khi và chỉ khi $AT$ tiếp xúc với $(ABC)$
b. Bổ đề. Cho $(O)$ và hai điểm $A, B$ nằm ngoài nó. Qua $A, B$ kẻ các tiếp tuyến $AC, AD, BE, BF$. $CD$ cắt $EF$ tại $G$. Lúc này $OG\perp AB$ tại $H$ thỏa $OG.OH=R^2$
Trong chủ đề: Tuần 4 tháng 11/2017: đường thẳng $AM$ luôn đi qua một điểm cố...
19-11-2017 - 21:32
Bài 1. Gọi $N$ là trung điểm $BC$, đường cao $BX, CY$. Ta có $MXNY$ là hình bình hành với $MX=NY$
Do đó $MXNY$ là hình thoi nên $MN|| AO$, còn có $\angle XNY$ không đổi nên $MN$ có độ dài không đổi.
Vậy $MA$ cắt $NO$ tại $S$ thì $\dfrac{SO}{SN}=\dfrac{AO}{MN}=\text{const}$, vậy $S$ cố định.
Trong chủ đề: Đề thi chọn đội tuyển Học sinh giỏi môn Toán tỉnh Bình Thuận năm 2017 - 2018
03-11-2017 - 13:37
Cho $y=0$ ta suy ra $f(x)=\frac{f(f(x))+f(0)}{f(0)+1}$ => $f$ toàn ánh => $\exists a:f(a)=0$ (với $a$ thuộc R)
Cho $x=y$ ta suy ra $f(f(0))=(f(x))^{2}-x^2$ $(1)$
giả sử $f(x_{1})=f(x_{2})$ thì từ $(1)$ suy ra $x^{2}_{1}=x^{2}_{2}$
TH1: $x_{1}=x_{2}$ => $f$ song ánh
thay $x=0$ và $y=a$ ta được $f(f(-a))=f(0)$ => $f(-a)=0=f(a)$ => $a=0$
như vậy $f(0)=0$ thế điều này vào $(1)$ ta được $(f(x))^{2}=x^2$
TH2:$x_{1}=-x_{2}$
Cũng thay $x=0$ , $y=a$ ta thu được $f(-a)=f(a)=0$
giả sử $a \neq 0$ thì thay $x=a$ vào $(1)$ ta thu được $f(f(0))=-a^{2}$ => $(f(x))^2=x^2-a^2$
đến đây thay $x=0$ ta thu được $((f(0))^2=-a^2 < 0$ => vô lý
do đó $a=0$ tương tự trường hợp 1 ta thu được $(f(x))^{2}=x^2$
thử hai trường hợp $f(x)=x$ và $f(x)=-x$ ta chỉ nhận $f(x)=x$
Chỗ bôi đỏ sai. Nếu mà từ đó suy ra toàn ánh thì suy được ra $f(x)=ax+b$ rồi
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Bài viết: dogsteven



 Tìm kiếm
Tìm kiếm