99AnhKhoa

Câu a:

Dễ thấy $DM= DN$. Vì vậy ta cần chứng minh $DE=DF$.

Ta có: 

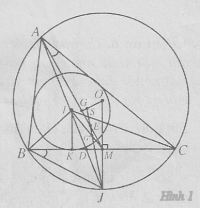
$\angle EDO=\angle EBO=90^{\circ}$ $\Rightarrow EBDO$ là tg nội tiếp $\Rightarrow \angle DEO=\angle DBO$.

$\angle FDO=\angle FCO=90^{\circ}$ $\Rightarrow FDOC$ là tg nội tiếp $\Rightarrow \angle DFO=\angle DCO$.

Mà $\angle DBO=\angle DCO$ $\Rightarrow \angle DEO=\angle DFO \Rightarrow \Delta OEF$ cân $\Rightarrow DE=DF$.

Câu b:

Theo chứng minh câu a, dễ thấy $\angle FEO=\angle CBO=\angle FAO$ $\Rightarrow AEFO$ là tứ giác nội tiếp.

Như vậy đường tròn ngoại tiếp $\Delta AEF$ luôn đi qua điểm $O$ cố định.

Áp dụng bất đẳng thức AM-GM:
$1+\frac{1}{a_{1}}\geqslant 2\sqrt{\frac{1}{a_{1}}}$

Làm tương tự ta được:

$\sqrt{1+\frac{1}{a_{1}}}+\sqrt{1+\frac{1}{a_{2}}}+...+\sqrt{1+\frac{1}{a_{n}}}\geqslant \sqrt{2}\left ( \sqrt[4]{\frac{1}{a_{1}}}+\sqrt[4]{\frac{1}{a_{2}}}+...+\sqrt[4]{\frac{1}{a_{n}}} \right )$

Tiếp tục áp dụng bất đẳng thức AM-GM:
$\sqrt{2}\left ( \sqrt[4]{\frac{1}{a_{1}}}+\sqrt[4]{\frac{1}{a_{2}}}+...+\sqrt[4]{\frac{1}{a_{n}}} \right )\geqslant n\sqrt{2} \sqrt[4n]{\frac{1}{a_{1}a_{2}...a_{n}}}=n\sqrt{2}$

Vậy $MinP=n\sqrt{2}$. 

Dễ dàng chứng minh được $HA$ là phân giác trong của $\Delta MHN$

Đồng thời $HC$ vuông góc với $HA$ $\Rightarrow$ $HC$ là phân giác ngoài của $\Delta MHN$

Theo tính chất đường tròn bàng tiếp tam giác, ta có:

$HC,NC$ là phân giác ngoài của $\Delta MHN$ $\Rightarrow$ $MC$ là phân giác trong của $\Delta MHN$

Đồng thời $MB$ là phân giác $\angle HME$ $\Rightarrow MC$ vuông góc $MB$ $\Rightarrow MC$ song song $HE$

Tương tự với $NB$.

Biến đổi tương đương bđt đầu bài cho ta được:

 $a(b^2+c^2)+b(c^2+a^2)+c(a^2+b^2)+2abc\geqslant 4(a+b+c)-4abc$

$\Leftrightarrow a(b+c)^2+b(a+c)^2+c(a+b)^2\geqslant 4(a+b+c)$

Áp dụng bđt Cauchy: $a(b+c)^2+4bc\geqslant 2\sqrt{4abc(b+c)^2}=4(b+c)$

Làm tương tự rồi cộng từng vế 3 bđt, ta được:

 $a(b+c)^2+b(a+c)^2+c(a+b)^2+4(ab+bc+ca)\geqslant 8(a+b+c)$

$\Leftrightarrow 2a(b+c)^2+2b(a+c)^2+2c(a+b)^2+8(ab+bc+ca)\geqslant 16(a+b+c)$   $\left ( 1 \right )$

Tiếp tục dùng Cauchy: $a(b+c)^2+4a\geqslant 2\sqrt{4a^2(b+c)^2}=4a(b+c)$

Làm tương tự rồi cộng từng vế 3 bđt, ta được:

 $8(ab+bc+ca)\leqslant a(b+c)^2+b(a+c)^2+c(a+b)^2+4(a+b+c)$   $\left ( 2 \right )$

Từ $\left ( 1 \right )$ và $\left ( 2 \right )$ $\Rightarrow 3a(b+c)^2+3b(a+c)^2+3c(a+b)^2+4(a+b+c)\geqslant 16(a+b+c)$

                     $\Rightarrow a(b+c)^2+b(a+c)^2+c(a+b)^2\geqslant 4(a+b+c)$   $\left ( dpcm \right )$

Dấu bằng: $a=b=c=1$

Câu a: $VT=(a+b+c)(ab+bc+ca)-abc=(a+b+c)(ab+bc+ca)-1$

Cauchy $\Rightarrow ab+bc+ca\geq 3 \Rightarrow VT\geq 3(a+b+c)-1$

Thay vào thì bđt tương đương với: $a+b+c\geq 3$ (luôn đúng theo Cauchy)

Dấu bằng: $a=b=c=1$