kimchitwinkle

Khảo sát min, max của $P=x^2+y^2-12x+16y$ trên miền $x^2+y^2 \leq 25$.

Cho hai số thực $x$, $y$ thỏa $x+y=\sqrt{x+1}+\sqrt{2y+2}$. Tìm giá trị nhỏ nhất và lớn nhất của:

$$P=x^2+y^2+2(x+1)(y+1)+\sqrt{4-x-y}.$$

Bài 1 có thể mở rộng theo hướng của bạn Nguyễn Trần Hữu Thịnh đã đăng trên Bài toán hay - Lời giải đẹp - Đam mê toán học ở Facebook như sau:

Bài toán. Cho $\triangle ABC$ nội tiếp đường tròn $\Gamma$ tâm $O$. Một đường tròn đi qua $B$, $C$ cắt $AB$ ,$AC$ lần lượt tại $F$, $E$. $(AEB)$ cắt $(AFC)$ tại $D$. $(DEF)$ cắt $AB$, $AC$ lần thứ hai theo thứ tự tại $M$, $N$. $MN$ cắt tiếp tuyến ở $A$ của $\Gamma$ tại $P$. $(AEF)$ cắt $\Gamma$ tại $Q \neq A$. $AQ$ cắt $EF$ tại $R$. Chứng minh rằng $PR \perp OH$ với $H$ là giao điểm của $BE$ và $CF$.

Mình xin đưa ra một mở rộng cho bổ đề trên:

Bài toán. Cho $\triangle ABC$ nhọn. $D$ là một điểm bất kì trên cạnh $BC$. Từ $D$ kẻ các đường thẳng song song $AB$, $AC$ lần lượt cắt $AC$, $AB$ tại $E$, $F$. Trên tia đối của các tia $FB$, $EC$ lần lượt lấy $N$, $M$ sao cho $\dfrac{NF}{LF}=\dfrac{DC}{DB}=\dfrac{EK}{EM}$. Đường tròn $(J)$ đi qua $A$ tiếp xúc $BC$ tại $D$. Gọi $I$ là tâm của $(AMN)$. Chứng minh rằng $AD$, $MN$, $IJ$ đồng quy.

Gần đây mình phát hiện một số mở rộng cho bài toán này, trước hết mình xin đưa ra một lời chứng minh thuần túy không dùng đến phép nghịch đảo đối với bổ đề mà thầy Hùng đã đề cập ở tuần 5 tháng 8 năm 2016. Mình xin ghi lại bổ đề:

Bổ đề. Cho $\triangle ABC$ nhọn. Gọi $D$, $E$, $F$ lần lượt là trung điểm của $BC$, $CA$, $AB$. Đường tròn $(J)$ đi qua $A$ và tiếp xúc với $BC$ tại $D$ cắt $AC$, $AB$ lần lượt tại $K$, $L$. Gọi $M$, $N$ lần lượt là điểm đối xứng của $K$, $L$ qua $E$, $F$. Cuối cùng gọi $I$ là tâm của $(AMN)$. Khi đó $AD$, $MN$, $IJ$ đồng quy.

Chứng minh. Kéo dài $DE$, $DF$ cắt $(J)$ theo thứ tự tại $Y$, $Z$. Ta chứng minh $Y$, $M$, $N$, $Z$ thẳng hàng.
Thật vậy, ta có:
$$\overline{AM}\cdot\overline{AC}=\overline{KC}\cdot\overline{AC}=CD^2=BD^2=\overline{LB}\cdot\overline{AB}=\overline{AN}\cdot\overline{AB}$$
Do đó tứ giác $BCMN$ nội tiếp. Ta lại có:
$$\overline{EY}\cdot\overline{ED}=\overline{EA}\cdot\overline{EK}$$
$$\Leftrightarrow \overline{EY}\cdot\overline{AB}=\overline{EM}\cdot\overline{AC}$$
$$\Leftrightarrow \dfrac{\overline{EY}}{\overline{EM}}=\dfrac{\overline{AC}}{\overline{AB}}=\dfrac{\overline{AN}}{\overline{AM}}$$
Mặt khác $AN \parallel EY$ nên theo định lý Thales đảo ta có $Y$, $M$, $N$ thẳng hàng. Tương tự $Z$, $M$, $N$ thẳng hàng hay bốn điểm $Y$, $M$, $N$, $Z$ cùng nằm trên một đường thẳng.

Tới đây mình có hai cách để giải quyết tiếp bài toán:

Cách 1. Thông qua biến đổi góc, ta có:
$$\widehat{AIN}=2\widehat{AMN}=2\widehat{YZD}=\widehat{YJD}$$
Suy ra $\triangle AIN \backsim \triangle DJY$. Như thế ta được:
$$\dfrac{AI}{JD}=\dfrac{AN}{YD}=\dfrac{AP}{PD}$$
Mặt khác do $MN$ đối song $BC$ nên $AI \text{ } \bot \text{ } BC \text{ } \bot \text{ } JD$ hay $AI \parallel JD$. Áp dụng định lý Thales đảo ta thu được $I$, $P$, $J$ thẳng hàng. Ta kết luận $AD$, $MN$, $IJ$ đồng quy.

Cách 2. Gọi $T$ là giao điểm của $EF$ và $YZ$. Gọi $S$ là giao điểm của $AT$ và $(J)$. Dễ thấy các tứ giác $EFZY$ và $MNFE$ nội tiếp. Ta có:
$$\overline{TS}\cdot\overline{TA}=\overline{TZ}\cdot\overline{TY}=\overline{TF}\cdot\overline{TE}=\overline{TN}\cdot\overline{TM}$$
Như vậy $ASNM$ nội tiếp. Do đó $AS \text{ } \bot \text{ } IJ$. Để chứng minh $I$, $P$, $J$ thẳng hàng thì ta cần chứng minh thêm $AS \text{ } \bot \text{ } IP$. Thật vậy, thông qua biến đổi góc:
$$\widehat{ANP}=\widehat{ZYD}=\widehat{ZAP}$$
Do đó $\triangle ZAP \backsim \triangle ANP$. Suy ra $PA^2=\overline{PN}\cdot \overline{PZ}$. Tương tự $PA^2=\overline{PM}\cdot \overline{PY}$.
Bây giờ ta chứng minh $(SNZ)$ tiếp xúc $(SMY)$. Thật vậy:
$$\widehat{SZN}+\widehat{SYM}=180^o-\widehat{ZSY}=\widehat{ZDY}=\widehat{MAN}=\widehat{MSN}$$
Vậy $(SNZ)$ tiếp xúc $(SMY)$. Suy ra $PS^2=\overline{PN}\cdot \overline{PZ}=\overline{PM}\cdot \overline{PY}=PA^2$. Do đó $\triangle SAP$ cân tại $P$. Vậy $AS \text{ } \bot \text{ } IP$ hay $I$, $P$, $J$ thẳng hàng. Ta kết luận $AD$, $MN$, $IJ$ đồng quy.

Một cách phát biểu khác tương đương với bài toán của thầy Hùng, ở đây $D$ là điểm bất kì và thay đường trung tuyến bằng đường đẳng giác của $AD$:

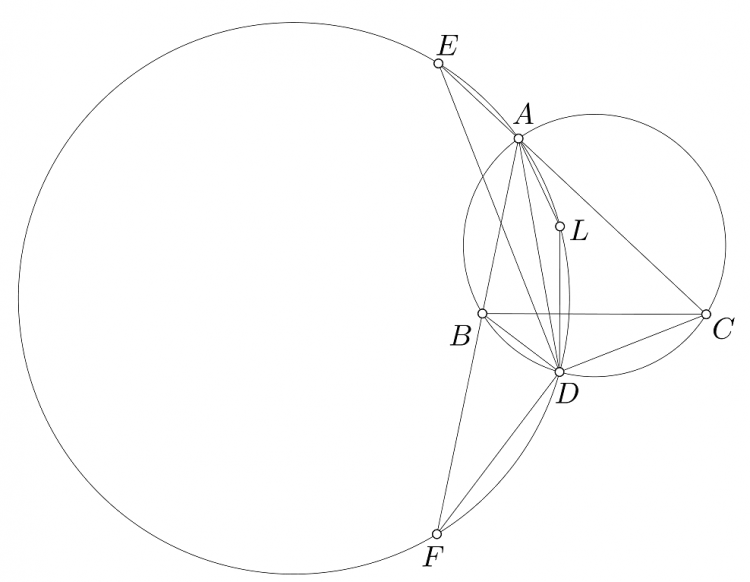
Cho $\triangle ABC$ nội tiếp $(O)$ và $D$ là một điểm nằm trên $(O)$. Trên đường thẳng $CA$, $AB$ lần lượt lấy $E$, $F$ sao cho $CD \text{ } \bot \text{ } ED$, $BD \text{ } \bot \text{ } FD$. Đường thẳng qua $D$ vuông góc $BC$ cắt đường đẳng giác của $AD$ đối với $\triangle ABC$ tại $L$. Khi đó $L$ nằm trên đường tròn $(ADFE)$.

Bài toán của thầy Hùng hoàn toàn có thể giải theo ý tưởng của em, vì thực chất, tính đối trung không còn cần thiết lắm ở câu (b). Thay vào đó là tính song song khá quan trọng $AH \parallel LD$.

Câu (b) ở trên là em lấy ý tưởng từ một tính chất trong tài liệu "Điểm cố định" của tác giả Nguyễn Trần Hữu Thịnh tại đây: http://simplegeometr...-quanh-hai.html

Mình xin đưa ra lời giải khác cho Câu 6:
Để ý hai điểm $B$, $C$ không có tác dụng gì ngoài việc tượng trưng $BC$ là tiếp tuyến của $D$ đối với $(I)$ thôi.
Do đó ta viết lại cấu hình bài toán như sau: Cho $\triangle DEF$ nội tiếp $(I)$, trực tâm $H$. Gọi $K$ là hình chiếu của $H$ lên tiếp tuyến tại $D$ của $(I)$. Tiếp tuyến tại $E$ và $F$ của $(I)$ cắt nhau tại $A$.

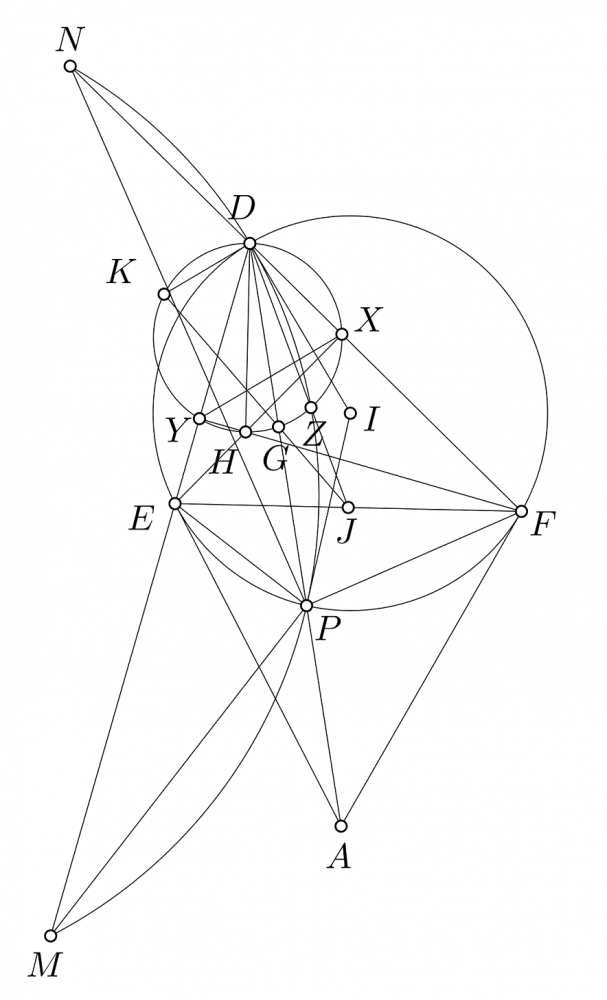
a) Kéo dài $EH$, $FH$ cắt $DF$, $DE$ lần lượt tại $X$, $Y$. Gọi $G$ là giao điểm của $KJ$ với $(T)$. Ta chứng minh $A$, $T$, $D$ thẳng hàng, tức là chứng minh $DT$ là đường đối trung của $\triangle DEF$. Vì $KD \parallel XY \text{ } \bot \text{ } DO$ nên $DKYX$ là hình thang cân. Do $J$ là giao điểm của tiếp tuyến tại $X$ và $Y$ của $(T)$ nên $KG$ là đường đối trung của $\triangle KXY$. Suy ra $\dfrac{GY}{GX}=\dfrac{KY}{KX}=\dfrac{DX}{DY}$. Suy ra $DG$ là đường trung tuyến của $\triangle DXY$. Mặt khác do $XY$ đối song $BC$ nên $DT$ là đường đối trung của $\triangle DEF$. Vậy $A$, $T$, $D$ thẳng hàng. Câu (a) được chứng minh.

b) Gọi $Z$ là giao điểm của $DJ$ và $(T)$. Trước khi chứng minh trọn vẹn bài toán, ta có một bổ đề khá đẹp về mối tương quan giữa trực tâm và đường trung tuyến như sau:

Bổ đề. Cho $\triangle ABC$ nội tiếp $(O)$, trực tâm $H$, $M$ là trung điểm của $BC$. $AM$ cắt $(O)$ tại $P$. Gọi $X$ là điểm đối xứng của $P$ qua $M$. Trên $(O)$ lấy $Q$ sao cho $AQ$ là đường đối trung của $\triangle ABC$. Khi đó $X$ là hình chiếu của $H$ lên $AM$ và $X$ là điểm đối xứng của $Q$ qua $BC$.

Chứng minh. Kẻ đường kính $AD$ của $(O)$. Do $BH \parallel CD \text{ } \bot \text{ } AC$ và $CH \parallel BD \text{ } \bot \text{ } AB$ nên tứ giác $BHCD$ là hình bình hành. Suy ra $MH=MD$. Mà $MX=MP$ nên $HXDP$ là hình bình hành. Do đó $HX \parallel PD \text{ } \bot \text{ } AP$ nên $X$ là hình chiếu của $H$ lên $AP$. Ta có $PQ \parallel BC$ nên $BCPQ$ là hình thang cân. Suy ra $MQ=MP=MX$ nên $XQ \text{ } \bot \text{ } PQ \parallel BC$. Từ đó ta kết luận $X$ là điểm đối xứng của $Q$ qua $BC$. Bổ đề được chứng minh.

Quay trở lại bài toán,

Áp dụng bổ đề cho $\triangle DEF$ được $Z$ thuộc $(T)$ và $ZP \parallel AH \text{ } \bot \text{ } BC$. Suy ra:
$$\widehat{DZP}=\widehat{DZH}+\widehat{HZP}=\widehat{DZH}+\widehat{DHZ}=180^o-\widehat{HDZ}=180^o-\widehat{PDI}=180^o-(90^o-\dfrac{1}{2}\widehat{DIP})=180^o-(90^o-\widehat{DFP})=180^o-\widehat{DNP}$$
Do đó $Z$ thuộc $(DNP)$. Tương tự $Z$ thuộc $(DMP)$. Vậy $Z$ thuộc $(MNP)$. Do $Z$, $D$ thuộc $(T)$ và $(MNP)$ nên $DZ \equiv DJ$ là trục đẳng phương của $(T)$ và $(MNP)$. Bài toán được chứng minh hoàn toàn.

Câu 3:

a) Ta chứng minh $A$, $H$, $O$ thẳng hàng để từ đó suy ra $OH \text{ } \bot \text{ } EH$. Tức là $H$ nằm trên đường tròn đường kính $OE$.
Thật vậy, thông qua biến đổi góc:
$$\widehat{EAO}+\widehat{AEF}=\widehat{AEO}+\widehat{EDF}=90^o$$
Do đó $AO \text{ } \bot \text{ } EF \text{ } \bot \text{ } AH$. Nên $A$, $H$, $O$ thẳng hàng. Suy ra $H$ nằm trên đường tròn đường kính $OE$. Vì $O$ và $E$ cố định nên ta có điều phải chứng minh.
b) Thật ra đây là một ứng dụng từ một bổ đề khá hay đối với đường tròn nội tiếp như sau:

Bổ đề. Cho $\triangle ABC$ ngoại tiếp $(I)$. $(I)$ tiếp xúc $BC$, $CA$, $AB$ lần lượt tại $D$, $E$, $F$. $ID$ cắt $EF$ tại $G$. Khi đó $AG$ đi qua trung điểm $M$ của $BC$.

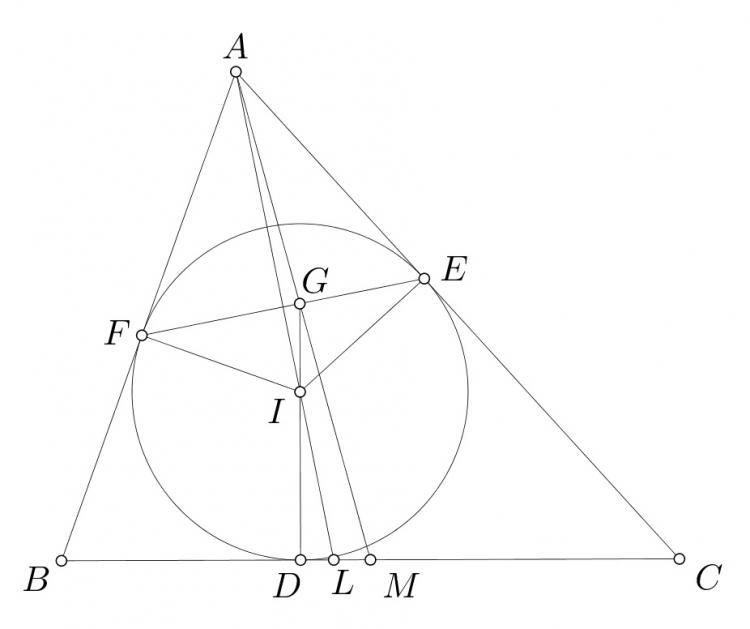
Chứng minh. Kéo dài $AI$ cắt $BC$ tại $L$. Ta có $\widehat{GFI}=\widehat{IAE}=\widehat{BAL}$ và $\widehat{FIG}=\widehat{FIA}+\widehat{AIG}=90^o-\widehat{FAI}+90^o-\widehat{ILD}=180^o-\widehat{FAI}-\widehat{ILD}=\widehat{ABL}$ nên $\triangle FIG \backsim \triangle ABL$, suy ra $\dfrac{FG}{FI}=\dfrac{AL}{AB} \Leftrightarrow AB\cdot FG=AL\cdot FI$. Tương tự $AC\cdot EG=AL\cdot EI$. Do $EI=FI$ nên $AB\cdot FG=AC\cdot EG \Leftrightarrow \dfrac{FG}{AC}=\dfrac{EG}{AB}$. Từ đây ta có:
$$\overrightarrow{AG}=\dfrac{FG}{EF}\overrightarrow{AE}+\dfrac{EG}{EF}\overrightarrow{AF}=\dfrac{FG}{EF}\cdot\dfrac{AE}{AC}\overrightarrow{AC}+\dfrac{EG}{EF}\cdot\dfrac{AF}{AB}\overrightarrow{AB}=k\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$$
Mặt khác do $\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$ nên ta được $A$, $G$, $M$ thẳng hàng.
Bổ đề được chứng minh.

Quay trở lại bài toán,

Kéo dài $AB$, $AC$ cắt $EF$ theo thứ tự tại $X$, $Y$. Gọi $K$ là trung điểm của $XY$. Do $PQ \text{ } \bot \text{ } EF$ nên $I$, $P$, $Q$ thẳng hàng. Áp dụng bổ đề cho $\triangle AXY$ được $AQ$ đi qua trung điểm $K$ của $XY$ hay $AQ$ là đường trung tuyến của $\triangle AXY$. Tiếp tục biến đổi góc:
$$\widehat{AYF}=\widehat{EAY}+\widehat{DEF}=\widehat{EAY}+\widehat{EDF}=\widehat{EAY}+\widehat{ADB}=180^o-\widehat{ABC}$$
Do đó tứ giác $BCYX$ nội tiếp hay $BC$ đối song $XY$. Như vậy $AQ$ là đường đối trung của $\triangle ABC$. Suy ra $AQ$ đi qua giao điểm $T$ cố định của tiếp tuyến tại $B$ và $C$ đối với $(O)$. Bài toán được giải quyết hoàn toàn.

Câu 5: Ta chia hai trường hợp:
Trường hợp 1: $p_i \neq 3, \forall i=\overline{1, 2016}$. Ta có:
$$\displaystyle{\sum\limits_{i=1}^{2016}\dfrac{1}{p_i^2+1}=\dfrac{(p_2^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+(p_1^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+\cdots+(p_1^2+1)(p_3^2+1)\cdots(p_{2015}^2+1)}{(p_1^2+1)(p_2^2+1)\cdots(p_{2016}^2+1)}}$$
Xét:
$$(p_2^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+(p_1^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+\cdots+(p_1^2+1)(p_3^2+1)\cdots(p_{2015}^2+1) \equiv (-1)^{2015}\cdot2016 \equiv 0 \text{ (mod }3)$$
$$(p_1^2+1)(p_2^2+1)\cdots(p_{2016}^2+1) \equiv (-1)^{2016} \equiv 1 \text{ (mod }3)$$
Do đó không thể có dạng $\dfrac{1}{n^2}$.
Trường hợp 2: $p_1=3, p_i \neq 3, \forall i=\overline{2, 2016}$. Ta có:
$$(p_2^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+(p_1^2+1)(p_3^2+1)\cdots(p_{2016}^2+1)+\cdots+(p_1^2+1)(p_3^2+1)\cdots(p_{2015}^2+1) \equiv 1\cdot(-1)^{2014}\cdot2015+(-1)^{2015} \equiv 1 \text{ (mod }3)$$
$$(p_1^2+1)(p_2^2+1)\cdots(p_{2016}^2+1) \equiv 1\cdot(-1)^{2015} \equiv -1 \text{ (mod }3)$$
Do đó không thể có dạng $\dfrac{1}{n^2}$.
Vậy ta có điều phải chứng minh.

Mình xin đưa ra hướng giải quyết ở một số bài:
Câu 1: Chứng minh $x_n \in \left(1; \dfrac{3}{2}\right)$. Sau đó chứng minh $(x_n)$ giảm. Ta dự đoán giới hạn của dãy là $\lim x_n=1$. Thật vậy nếu $\lim x_n=a>1$. Đặt $a=1+\varepsilon$. Thay $x$ bởi $a$ và $n$ bởi $n-2$ vào phương trình, kết hợp rút gọn được:
$$\dfrac{(1+\varepsilon)^{n-1}-1}{\varepsilon}=n \Leftrightarrow (1+\varepsilon)^{n-1}=n\varepsilon+1$$
Ta cần chứng minh điều vô lý ở đây, theo cảm nhận ta thấy khi $n$ đủ lớn thì $VT > VP$. Ta sẽ chứng minh điều này.
Thật vậy:
$$(1+\varepsilon)^{n-1}>1+(n-1)\varepsilon+\dfrac{(n-1)(n-2)}{2}\varepsilon^2$$
Vậy ta cần chứng minh:
$$1+(n-1)\varepsilon+\dfrac{(n-1)(n-2)}{2}\varepsilon^2>n\varepsilon+1 \Leftrightarrow \dfrac{(n-1)(n-2)}{2}\varepsilon^2>\varepsilon$$
Cho $n \to + \infty$ ta có ngay bất đẳng thức trên. Vậy ta suy ra điều vô lý. Do đó $a=1$ hay $\lim x_n=1$.

Mình up các bài còn lại sau...

VÒNG 2

vÒNG 1

em cũng không đồng tình thi Toán trắc nghiệm   mà khéo thi trắc nghiệm chắc gì mấy ông ở bộ cho dùng máy tính  ví dụ thủ các đáp án cứ loằng ngoằng cả có thể làm được mà chắc gì đủ thời gian làm hết 

Sống thật với bản thân   không qua chỉnh sửa