halloffame

$3/$ Áp dụng phép vị tự tâm $A$ tỉ số $\frac{AC}{AF}$ ta đưa bài toán đã cho về bài toán sau:

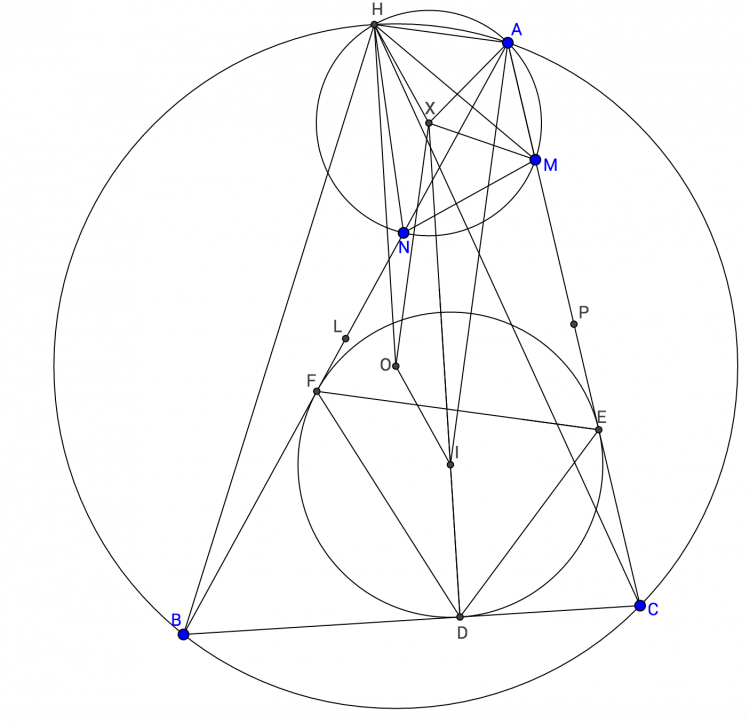
Bài toán 3'. Cho tam giác $ABC$ nội tiếp $(O),$ trực tâm $H,$ trung tuyến $AM,$ đường cao $AD,BE,CF.$ Tiếp tuyến tại $A$ của $(O)$ cắt $BC$ ở $S,G$ là trung điểm $AH.$

$a)$ Chứng minh $SG \perp AM.$

$b)$ Đường thẳng qua $A$ vuông góc $AB,AC$ cắt $BH,CH$ tại $I,J.K,L$ là trung điểm $IC,JB.$ Chứng minh $OS \parallel KL.$

Giải.

$a) AOMG$ là hình bình hành $\Rightarrow MG \perp SA \Rightarrow G$ là trực tâm $\Delta AMS \Rightarrow SG \perp AM.$

$b)$

Bổ đề. $\Delta ABC$ nội tiếp $(O),M$ trung điểm $BC.$ Đường thẳng qua $B,C$ vuông góc $AB,AC$ cắt $AC,AB$ tại $G,H.$ Đường thẳng qua $A$ vuông góc $AB,AC$ cắt đường thẳng qua $B,C$ đối xứng $AC,AB$ qua trung trực $AB,AC$ tại $E,F.$ Khi đó $AM$ là trục đẳng phương của $(ECG),(FBH).$

Chứng minh. Do đường thẳng $AF,CF$ đối xứng đường thẳng $CH,AH$ qua trung trực $AC$ nên $ACHF$ là hình chữ nhật, suy ra $CF,(O),(BHF)$ đồng quy tại $L$ và $ACBL$ là hình thang cân. Tương tự ta có $(O) \cap (ECG)=K$ và $ABCK$ là hình thang cân.

Gọi $D=LB \cap CK$ thì $ABDC$ là hình bình hành $\Rightarrow \overline{A,D,M}.$ Lại có $BL,CK$ là trục đẳng phương $(O)$ và $(BHF),(O)$ và $(CKG)$

$\Rightarrow AM$ là trục đẳng phương $(BHF),(CGE).$

Quay lại bài toán.

$JA \perp AC,AH \perp BC,HJ \perp BA \Rightarrow \Delta JHA \sim \Delta ABC \Rightarrow JG \perp AM.$

Tương tự $IG \perp AM \Rightarrow \overline{S,G,I,J}.$ Vẽ $A'$ đối xứng $A$ qua $SO$ thì $AA'$ là đường đối trung $\Delta ABC.$

Gọi đường thẳng qua $B,C$ vuông góc $AB,AC$ cắt $CA,AB$ tại $N,P;$ đường thẳng qua $A$ vuông góc $AB,AC$ cắt đường thẳng qua $B,C$ đối xứng $AC,AB$ qua trung trực $AB,AC$ tại $Q,R.$

Xét phép biến hình $f$ là hợp của phép nghịch đảo tâm $A$ phương tích $AB.AC$ hợp với phép đối xứng qua phân giác $\widehat{BAC}.$

Ta có $f(B)=C,f(C)=B,f(F)=N,f(E)=P,f(A')=M.$ Do $\widehat{QBA}= \widehat{BAC}= \widehat{CJA} \Rightarrow \Delta AQB \sim \Delta ACJ$

$\Rightarrow AQ.AJ=AB.AC$ và $\widehat{QAC}= \widehat{BAJ} \Rightarrow f(J)=Q.$ Tương tự $f(I)=R \Rightarrow f((JFB))=(CNQ),f((CEI))=(JBP).$

Theo bổ đề $AM$ là trục đẳng phương $(CNQ),(JBP)$ nên qua phép biến hình $f$ thì $AA'$ là trục đẳng phương $(JFB),(CEI)$

$\Rightarrow A'A \perp KL \Rightarrow OS \parallel KL.$

Ta có đpcm.

Bài hình ngày 1:

$a)$ 

$\frac{AB}{\sin \widehat{AGB}}= \frac{AG}{\sin \widehat{ABG}}= \frac{AG}{\sin \widehat{BAN}}; \frac{AC}{\sin \widehat{AHC}}= \frac{AH}{\sin \widehat{ACH}}= \frac{AH}{\sin \widehat{BAN}}.$

Lại có $\widehat{AGB}= \widehat{GAN}= \widehat{QAH}= \widehat{AHC} \Rightarrow \frac{AG}{AH}= \frac{AB}{AC}= \frac{AN}{AQ}$

$\Rightarrow AQ.AG=AN.AH \Rightarrow A \in FE$ là trục đẳng phương của $(GMQ),(HNP).$

Ta có đpcm.

$b)$

$\widehat{MEQ}=180^0- \widehat{MGQ}=180^0- \widehat{NHP}= \widehat{NEP} \Rightarrow \widehat{MEN}= \widehat{QEP}.$

Gọi $MN$ cắt $PQ$ tại $F_1$ thì $\widehat{F_1}= \widehat{BAC}= 360^0- \widehat{NAB}- \widehat{QAC}- \widehat{NAQ}=360^0- \widehat{ACP}- \widehat{QAC}-180^0+ \widehat{QAH}= \widehat{AHC}= \widehat{AGB}$

$\Rightarrow F_1 \in (MEQ) \cap (NEH) \Rightarrow F_1 \equiv F \Rightarrow \widehat{NME}=180^0- \widehat{F}= \widehat{EPQ} \Rightarrow \Delta  EMN \sim \Delta EQP.$

Do đó tồn tại một phép vị tự quay $X$ tâm $E$ sao cho $X(M)=Q,X(N)=P.$ Lại có hai hình bình hành $ABMN,CAQP$ đồng dạng nhau nên

$X(B)=A,X(A)=C \Rightarrow \Delta EBA \sim \Delta EAC \Rightarrow \widehat{BEC}= \widehat{BAC}+ \widehat{ABE}+ \widehat{ACE} = \widehat{BAC}+ \widehat{BAE}+ \widehat{EAC}=2 \widehat{BAC}= \widehat{BOC}$

$\Rightarrow O,B,E,C$ đồng viên. Ta có đpcm.

$1/$

Gọi $L'$ đối xứng $L$ qua $BI,DL'$ cắt $KL$ tại $F.$

Ta có $DI=EI \Rightarrow \widehat{DBI}= \widehat{IBE}= \widehat{IBK} \Rightarrow \Delta DBI= \Delta KBI \Rightarrow D$ đối xứng $K$ qua $BI.$

Do đó $F \in BI,$ lại có $\overline{D,T,L} \Rightarrow \overline{K,T,L'} \Rightarrow T$ thuộc đối cực của $F$ đối với $(I) \Rightarrow FP$ tiếp xúc $(I).$

Ta có đpcm. 

Nhân dịp sắp kết thúc năm 2017 và tiến tới VMO 2018, đồng thời Marathon HH đạt mốc 200 bài, mình thay mặt BQT và các ĐHV gửi lời cảm ơn tới các thành viên của diễn đàn đã và đang theo dõi, giải bài trong Marathon HH. Sau đây là danh sách các bài toán trong Marathon chưa có lời giải.

$$\begin{array}{| l | l |} \hline Bài & Người đăng\\ \hline 162 & quanghung86\\ \hline 196 & ecchi123\\ \hline 197 & DucLuong91\\ \hline 199 & dogsteven\\ \hline 200 & SonKHTN1619\\ \hline \end{array}$$

a) $L,P$ là trung điểm $AB,AC.$ Theo định lí bốn điểm,

$(MO^2-NO^2)-(MI^2-NI^2)=(MP^2+PO^2-NL^2-LO^2)-(BI^2-CI^2)= \frac{(MC-MA)^2-(NB-NA)^2+BA^2-CA^2}{4}-(BD^2-CD^2)$

$= \frac{(2BC-AC)^2-(2BC-AB)^2+BA^2-CA^2}{4}-(BD^2-CD^2)= \frac{(2BC-2AC)2BC-(2BC-2AB)2BC}{4}-BC(BD-CD)$

$=(BC-AC)BC-(BC-AB)BC-BC(BD-CD)=BC(BC-AC-BC+AB-BD+CD)=0 \Rightarrow$ đpcm.

b) $H=(AMN) \cap (ABC), H \neq A.$

$\widehat{HNB}=180^0- \widehat{HNA}=180^0- \widehat{HMA}= \widehat{HMC}, \widehat{HBN}= \widehat{HCN}$

$\Rightarrow \Delta HNB \sim \Delta HNC.$ Mà $NB=BC=CM \Rightarrow \Delta HNB= \Delta HMC$

$\Rightarrow HB=HC,HM=HN \Rightarrow HX \perp MN,HO \perp BC.$

Theo định lí bốn điểm, $BX^2-CX^2=(BX^2-R_X^2)-(CX^2-R_X^2)=BN.BA-CM.CA=BC(BA-AC)=BC(BD-DC)=BD^2-CD^2$

$\Rightarrow XD \perp BC \Rightarrow HX \parallel OI,HO \parallel IX \Rightarrow OI=HX=R_X.$ (đpcm)

c) $HB=HC \Rightarrow HA \perp AI \Rightarrow AI \parallel XO.$ 

Ta có $AX=OI$ nên $AXOI$ là hình bình hành hoặc hình thang cân.

Nếu $AXOI$ là hình bình hành thì $A \equiv H \Rightarrow AB=AC$ vô lí, nên $AXOI$ là hình thang cân $\Rightarrow A,X,O,I$ đồng viên. (đpcm)

Xét phép nghịch đảo tâm $A$ phương tích bất kì, ta chuyển bài toán đã cho về bài toán phụ:

Bài toán phụ. Cho tam giác $ABC,A_1$ là điểm bất kì $,B_1$ là điểm bất kì trên $BA_1,(BCB_1)$ cắt $A_1C$ ở $C_1.$ 

Chứng minh tiếp tuyến tại $A_1$ của $(AB_1C_1)$ song song với $BC.$

Bài toán phụ được chứng minh bằng cách gọi $A_1a$ là tiếp tuyến $(AB_1C_1)$ và có biến đổi góc 

$\widehat{aA_1C_1}= \widehat{A_1B_1C_1}= \widehat{A_1CB}$ suy ra đpcm.

Tìm tập xác định và đạo hàm của hàm số $y=f(x)$ thoả mãn phương trình $y \sin x= \ln (x^3-2y^4).$

Gọi $MP$ cắt $NQ$ ở $A,MP$ cắt $IC$ ở $B,MN$ cắt $PQ$ ở $C,CJ$ cắt $QN$ ở $D.$

Sử dụng các tam giác đồng dạng, ta suy ra được $\frac{IB}{IC}= \frac{CD}{CJ} = \frac{BA}{CJ}.$

Theo định lí Thales, $\overline{A,I,J}$ (đpcm).

-khi vào phòng thi thì không có máy tính cầm tay nên rất khó để đoán được $n=6$ thỏa mãn, $n=7$ không thỏa mãn, vì vậy, 1 vấn đề ở đây là phải tìm cách chứng tỏ rằng $n=6$ thỏa mãn và $n=7$ không thỏa mãn, sau đó thực hiện bước quy nạp và kết luận.

Mình làm bài này hoàn toàn không dùng tới máy tính, vì số không quá lớn.

Bạn có thể để ý rằng $11^n$ sẽ tăng mạnh hơn $1^n+2^n+...+10^n$ nên có thể dự đoán là tồn tại một số $k$ mà mọi $n>k$ không thoả mãn.

Với $n=1 \rightarrow 7$ thì mình tính tay mất gần 8 phút, và nếu xét đến thời gian 180 phút của một kì thi thông thường thì con số này chẳng thấm vào đâu.

IMO Shortlist 2012.

Ta thấy $n=1,2,..,6$ thoả mãn nhưng $1^7+2^7+3^7+...+10^7<11^7.$

Ta quy nạp để chứng minh mọi $n>7$ không thoả mãn. 

Giả sử $1^k+2^k+3^k+...+10^k<11^k(k \in \mathbb{N^*})$ thì:

$11^{k+1}=11^k.11>(1^k+2^k+3^k+...+10^k).11>1^{k+1}+2^{k+1}+3^{k+1}+...+10^{k+1}.$

Theo nguyên lí quy nạp ta có đpcm, tức chỉ có $n=1,2,...,6$ thoả mãn bài toán.

$CX$ cắt $(O)$ ở $G \neq C,BG$ cắt $AC$ ở $Y',AG$ cắt $BC$ ở $D.$ Xét cực và đối cực với $(O).$

$XY'$ là đối cực $D,$ mà $D \in BC$ là đối cực $T$ nên $T$ thuộc đối cực $D$ là $XY'.$

Vậy $X,T,Y'$ thẳng hàng nên $Y \equiv Y'$ và ta có đpcm. 

Bài toán 177 :  Cho tứ giác nội tiếp $ABCD$, $AB$ cắt $CD$ tại $P$, $AD$ cắt $BC$ tại $Q$. Chứng minh rằng khoảng cách giữa trực tâm hai tam giác $APD$ và $AQB$ bằng khoảng cách giữa trực tâm hai tam giác $CQD$ và $BPC$

Một lời giải khác của bạn dangkhuong cho bài toán 177:

Gọi $X,Y,Z,T$ lần lượt là trực tâm của các tam giác $APD,QDC,QAB,PBC.$

Vì $X,Y,Z,T$ thẳng hàng nên đpcm $\Leftrightarrow ZT=XY.$

Gọi $PX$ cắt $QY$ ở $F,K$ là hình chiếu của $Q$ lên $DC,O$ và $O'$ là tâm $(QDC)$ và $ABCD).$

$QK,QO$ đẳng giác $\Rightarrow QO \perp AB.$ Gọi $QO$ cắt $AB$ ở $J.$

$\Delta QAB \sim \Delta QCD \Rightarrow \Delta QZB \sim \Delta QYD \Rightarrow \frac{QZ}{QY}=\frac{QB}{QD}=\frac{QJ}{QK} \Rightarrow KJ \parallel YZ.$

$\widehat{XPD}=\widehat{DAX}=\widehat{SQA}=\widehat{ZQB} \Rightarrow \Delta FPK \sim \Delta BQJ \Rightarrow \frac{KF}{JB}=\frac{PK}{QJ}.$

Tứ giác $QJKP$ nội tiếp $\Rightarrow \Delta QJS \sim \Delta PKS \Rightarrow \frac{SJ}{SK}=\frac{QJ}{PK}=\frac{KF}{JB} \Rightarrow JK \parallel FB \Rightarrow FB \parallel YT.$

$\Rightarrow YTBF$ là hình bình hành $\Rightarrow YF=TB.$

Lại có $\Delta YXF \sim \Delta TZB \Rightarrow ZT=XY.$

Ta có đpcm.

Lời giải bài toán 195. Xem tại đây.

Hiện tại mình không có bài mới, mọi người đề nghị bài mới giúp mình.

Lời giải bài toán 183.

Bạn xem tại đây.