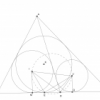
Lời giải bài 23:
a) Ta có $\Delta CMB=\Delta AMD(c.g.c)\Rightarrow \widehat{MAD}=\widehat{MCB},\widehat{MDA}=\widehat{MBC}\Rightarrow$ tứ giác $AMPC,BMPD$ nội tiếp.
b) $\widehat{CMP}=\widehat{CAP}=\widehat{PDM}=\widehat{CBM}\Rightarrow \Delta CMP\sim \Delta CBM(g.g)\Rightarrow CP.CB=CM^2=AM^2\Rightarrow \sqrt{CP.CB}=AM.$ Tương tự cũng có $\sqrt{DP.DA}=MB\Rightarrow \text{đpcm}$
Lời giải bài 24:
a) $\widehat{ADE}=\widehat{AHE}=\widehat{ECB}\Rightarrow$ tứ giác $BDEC$ nội tiếp.
b) $\widehat{SHD}=\widehat{BAH}=\widehat{SEH}\Rightarrow SB.SC=SH^2(=SD.SE)$
c) Lấy $K$ đối xứng $H$ qua $S$ thì $SO//AK$ hay $SM//AK$ suy ra $\frac{BM}{MA}=\frac{BS}{SK}=\frac{BS}{SH}$
Mặt khác, $SB.SC=SH^2\Rightarrow SB.HC=SH^2-SB.SH=SH.BH\Rightarrow \frac{BS}{SH}=\frac{BH}{HC}$ do đó $\frac{BM}{MA}=\frac{BH}{HC}\Rightarrow MH//AC$ hay $HP//EC.$ Từ đây suy ra tứ giác $BDPH$ nội tiếp $\Rightarrow BPH=\widehat{BDP}=90 ^{\circ}\Rightarrow BP \perp MH\Rightarrow BP \perp AC$
Cmtt, $CQ \perp AB$ suy ra đpcm.
Lời giải bài 25:
Dễ thấy $PQ$ đi qua trung điểm $K$ của $AB.$ Áp dụng định lí $Ceva$ cho tam giác $QAB$ có: $\frac{NA}{NQ}.\frac{KB}{KA}.\frac{MQ}{MB}=1\Rightarrow \frac{QN}{NA}=\frac{QM}{MB}\Rightarrow MN//AB.$ MÀ $PQ$ đi qua trung điểm của $AB$ do đó $PQ$ đi qua trung điểm của $MN.$



 Tìm kiếm
Tìm kiếm Nam
Nam