- HoangKhanh2002 và Tea Coffee thích
tpdtthltvp
Giới thiệu
Dù con đã qua rồi cái tuổi ngây thơ,
Nhưng với mẹ con lúc nào cũng còn nhỏ dại.
Muốn ôm con trong vòng tay mãi mãi,
Để mưa nắng cuộc đời mẹ gánh chịu vì con.
Thống kê
- Nhóm: Điều hành viên THCS
- Bài viết: 831
- Lượt xem: 14333
- Danh hiệu: Trung úy
- Tuổi: 21 tuổi
- Ngày sinh: Tháng sáu 14, 2002
-
Giới tính
 Nam
Nam
-
Đến từ
$\boldsymbol{\text{CVP}}$
Công cụ người dùng
Lần ghé thăm cuối
#683578 Đề tuyển sinh vào 10 THPT chuyên Vĩnh Phúc môn toán (chung)
 Gửi bởi tpdtthltvp
trong 07-06-2017 - 20:58
Gửi bởi tpdtthltvp
trong 07-06-2017 - 20:58
#671727 Topic ôn thi hình học vào cấp 3 chuyên
 Gửi bởi tpdtthltvp
trong 15-02-2017 - 20:51
Gửi bởi tpdtthltvp
trong 15-02-2017 - 20:51
Lời giải bài 23:
a) Ta có $\Delta CMB=\Delta AMD(c.g.c)\Rightarrow \widehat{MAD}=\widehat{MCB},\widehat{MDA}=\widehat{MBC}\Rightarrow$ tứ giác $AMPC,BMPD$ nội tiếp.
b) $\widehat{CMP}=\widehat{CAP}=\widehat{PDM}=\widehat{CBM}\Rightarrow \Delta CMP\sim \Delta CBM(g.g)\Rightarrow CP.CB=CM^2=AM^2\Rightarrow \sqrt{CP.CB}=AM.$ Tương tự cũng có $\sqrt{DP.DA}=MB\Rightarrow \text{đpcm}$
Lời giải bài 24:
a) $\widehat{ADE}=\widehat{AHE}=\widehat{ECB}\Rightarrow$ tứ giác $BDEC$ nội tiếp.
b) $\widehat{SHD}=\widehat{BAH}=\widehat{SEH}\Rightarrow SB.SC=SH^2(=SD.SE)$
c) Lấy $K$ đối xứng $H$ qua $S$ thì $SO//AK$ hay $SM//AK$ suy ra $\frac{BM}{MA}=\frac{BS}{SK}=\frac{BS}{SH}$
Mặt khác, $SB.SC=SH^2\Rightarrow SB.HC=SH^2-SB.SH=SH.BH\Rightarrow \frac{BS}{SH}=\frac{BH}{HC}$ do đó $\frac{BM}{MA}=\frac{BH}{HC}\Rightarrow MH//AC$ hay $HP//EC.$ Từ đây suy ra tứ giác $BDPH$ nội tiếp $\Rightarrow BPH=\widehat{BDP}=90 ^{\circ}\Rightarrow BP \perp MH\Rightarrow BP \perp AC$
Cmtt, $CQ \perp AB$ suy ra đpcm.
Lời giải bài 25:
Dễ thấy $PQ$ đi qua trung điểm $K$ của $AB.$ Áp dụng định lí $Ceva$ cho tam giác $QAB$ có: $\frac{NA}{NQ}.\frac{KB}{KA}.\frac{MQ}{MB}=1\Rightarrow \frac{QN}{NA}=\frac{QM}{MB}\Rightarrow MN//AB.$ MÀ $PQ$ đi qua trung điểm của $AB$ do đó $PQ$ đi qua trung điểm của $MN.$
- CaptainCuong, Nguyenphuctang và viet9a14124869 thích
#670485 Topic ôn thi hình học vào cấp 3 chuyên
 Gửi bởi tpdtthltvp
trong 30-01-2017 - 18:54
Gửi bởi tpdtthltvp
trong 30-01-2017 - 18:54
Bài 21: [Đề TS vào lớp 10 THPT Chuyên Ngoại Ngữ, Đại học Ngoại Ngữ, Đại học Quốc gia Hà Nội 2014 - 2015]
Cho tam giác ABC (AB < AC) nhọn nội tiếp (O). Kẻ đường cao AH. Gọi P, Q lần lượt là chân đường vuông góc kẻ từ H đến AB, AC.
a) Chứng minh: BCQP nội tiếp.
b) PQ kéo dài cắt BC tại M. Chứng minh : $MH^{2}=MB.MC$.
c) K là giao điểm của MA với đường tròn (O) (K khác A). I là tâm đường tròn ngoại tiếp tứ giác BCQP. Chứng minh rằng: I, H, K thẳng hàng.
Lời giải bài 21:
a) Ta có: $\widehat{APQ}=\widehat{AHQ}=\widehat{QCB}\Rightarrow \text{đpcm}$
b) $\widehat{MHP}=\widehat{BAH}=\widehat{MQH}\Rightarrow \Delta MHP\sim \Delta MQH\Rightarrow MH^2=MP.MQ$
c) $MH^2=MP.MQ=MB.MC=MK.MA\Rightarrow \Delta MHK\sim \Delta MAH\Rightarrow HK \perp AM(1)$
Gọi $S,T$ lần lượt là trung điểm của $BQ,CP.$ Ta có: $MP.MQ=MK.MA$ nên tứ giác $KAQP$ nội tiếp $\Rightarrow \widehat{KPA}=\widehat{KQA}\Rightarrow \widehat{KPB}=\widehat{KQC}$ mà $\widehat{KBA}=\widehat{KCA}\Rightarrow \widehat{KBP}=\widehat{KCQ}$ suy ra $\Delta KBP\sim \Delta KCQ\Rightarrow \Delta KSP\sim \Delta KTQ\Rightarrow \widehat{KSP}=\widehat{KTQ}\Rightarrow \widehat{KSA}=\widehat{KTA}$ suy ra tứ giác $KATS$ nội tiếp mà tứ giác $SATI$ nội tiếp do đó $5$ điểm $K,A,T,I,S$ cùng thuộc $1$ đường tròn. Do đó $\widehat{IKA}=\widehat{ISA}=90^{\circ}\Rightarrow IK \perp AM(2)$
Từ $(1),(2)$ suy ra $I,H,K$ thẳng hàng.
Bài 22 (Đề thi vào chuyên toán THPT chuyên Vĩnh Phúc 2013-2014):
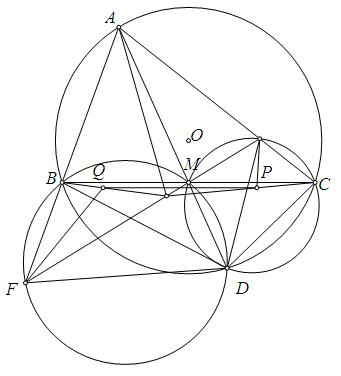
Cho tam giác $ABC$ nhọn $(AB<AC).$ Gọi $D,E,F$ lần lượt là chân các đường cao hạ từ $A,B,C.$ Gọi $P=BC\cap EF.$ Đường thẳng qua $D$ song song với $EF$ cắt $AB,AC,CF$ lần lượt tại $Q,R,S.$ Chứng minh rằng:
a) Tứ giác $BQCR$ nội tiếp.
b) $D$ là trung điểm của $QS.$
c) $(PQR)$ chia đôi $BC.$
- CaptainCuong yêu thích
#670247 Topic ôn thi hình học vào cấp 3 chuyên
 Gửi bởi tpdtthltvp
trong 28-01-2017 - 19:57
Gửi bởi tpdtthltvp
trong 28-01-2017 - 19:57
Bài 20: [Đề vào 10 chuyên Lê Qúy Đôn Đà Nẵng 2016 - 2017]
Cho tam giác ABC có $\widehat{BAC}> 90^{0}$, AB < AC và nội tiếp đường tròn tâm O. Trung tuyến AM của tam giác ABC cắt (O) tại điểm thứ hai D. Tiếp tuyến của (O) tại D cắt đường thẳng BC tại S. Trên cung nhỏ DC của (O) lấy điểm E, đường thẳng SE cắt (O) tại điểm thứ hai là F. Gọi P, Q lần lượt là giao điểm của các đường thẳng AE, AF với BC
a) Chứng minh rằng MODS là tứ giác nội tiếp
b) Chứng minh rằng QB = PC
Lời giải bài 20:
a) Tứ giác $MDOS$ có $\angle OMS=\angle ODS=90^{\circ}\Rightarrow $ $MDOS$ là tứ giác nội tiếp.
b) Gọi $T=FM\cap (O),P'=TD\cap AE.$ Áp dụng định lý $Pascal$ cho bộ $\begin{pmatrix} DET \\ FDA \end{pmatrix}$ ta được $M,P',S$ thẳng hàng. Do đó $P\equiv P'$ hay $FM,DP$ cắt nhau trên $(O).$
$AD,FT$ là $2$ dây cung đi qua trung điểm $M$ của dây cung $BC,$ $AF\cap BC=Q,TD\cap BC=P.$ Theo định lý con bướm ta có $MQ=MP$ suy ra $QB=PC.$
- duylax2412 yêu thích
#670182 Topic về phương trình và hệ phương trình
 Gửi bởi tpdtthltvp
trong 27-01-2017 - 22:14
Gửi bởi tpdtthltvp
trong 27-01-2017 - 22:14
Bài 553: Giải hệ phương trình:
$\left\{\begin{matrix} &2x+\dfrac{1}{x+y}+\dfrac{1}{x-y}=\dfrac{16}{3} \\ &2(x^{2}+y^{2})+\dfrac{1}{(x+y)^{2}}+\dfrac{1}{(x-y)^{2}}=\dfrac{100}{9} \end{matrix}\right.$
Ta có:
$HPT\Leftrightarrow \left\{\begin{matrix} [(x-y)+\frac{1}{x-y}]+[(x+y)+\frac{1}{x+y}]=\frac{16}{3} \\ [(x-y)+\frac{1}{x-y}]^2+[(x+y)+\frac{1}{x+y}]^2=\frac{136}{9} \end{matrix}\right.\Leftrightarrow \begin{bmatrix} (x-y)+\frac{1}{x-y}=2;(x+y)+\frac{1}{x+y}=\frac{10}{3} \\ (x-y)+\frac{1}{x-y}=\frac{10}{3}; (x+y)+\frac{1}{x+y}=2 \end{bmatrix}\Leftrightarrow\begin{bmatrix} x=\frac{2}{3},y=-\frac{1}{3} \\ x=\frac{2}{3},y=\frac{1}{3} \\ x=\frac{2}{3},y=-1 \\ x=2,y=1 \end{bmatrix}$
- tritanngo99, NTA1907 và ShenLongHkHT thích
#669831 Chứng minh rằng $MD,SI$ cắt nhau tại $1$ điểm nằm trên...
 Gửi bởi tpdtthltvp
trong 25-01-2017 - 10:24
Gửi bởi tpdtthltvp
trong 25-01-2017 - 10:24
Cho tam giác $ABC$ nội tiếp $(O),$ ngoại tiếp $(I).$ Đường tròn $(I)$ tiếp xúc $BC$ tại $D.$ Lấy $M$ là điểm chính giữa cung $BC,$ $S$ đối xứng $A$ qua $(O).$ Chứng minh rằng $MD,SI$ cắt nhau tại $1$ điểm nằm trên $(O).$
- hoakute yêu thích
#669795 Marathon số học THCS
 Gửi bởi tpdtthltvp
trong 24-01-2017 - 23:32
Gửi bởi tpdtthltvp
trong 24-01-2017 - 23:32
#669792 Marathon số học THCS
 Gửi bởi tpdtthltvp
trong 24-01-2017 - 23:09
Gửi bởi tpdtthltvp
trong 24-01-2017 - 23:09
Bài toán 3 : Tìm tất cả nghiệm nguyên dương của phương trình
$x^y+y^z+z^x=2(x+y+z)$
Giả sử cả $3$ số đều lớn hơn $1$ thì $x^y+y^z+z^x\geq x^2+y^2+z^2\geq \frac{(x+y+z)^2}{3}\geq 2(x+y+z)(\text{vì }x+y+z\geq 6).$ Dấu $"="$ xảy ra khi $x=y=z=2.$
Xét trường hợp có $1$ số là $1$, giả sử $x=1$ thì $y^z=1+2y+z.$ Dễ thấy $y\geq 2.$ Ta sẽ chứng minh với $y,z\in \mathbb{Z}_+,y\geq 2$ thì $y^z>1+2y+z(1).$ Thật vậy, giả sử $(1)$ đúng với $z=k$ thì $y^k>1+2y+k.$ Với $z=k+1,(1)\Leftrightarrow y^{k+1}>2+2y+k(2)$
Ta có $VT(2)>y(1+2y+k)=2y^2+yk+y.$ Mà $2y^2+yk+y>2+2y+k\Leftrightarrow 2(2y-1)+k(y-1)>2, \text{đúng}.$
Vậy $\left ( x,y,z \right )=\left ( 2,2,2 \right )$
#669787 Marathon số học THCS
 Gửi bởi tpdtthltvp
trong 24-01-2017 - 22:24
Gửi bởi tpdtthltvp
trong 24-01-2017 - 22:24
Bài toán 2 : Tìm mọi cặp số nguyên dương x , y sao cho $\frac{x^4+2}{x^2y+1}$ là số nguyên dương .
Ta có: $x^4+2\vdots x^2y+1\Rightarrow x^4y+2y\vdots x^2y+1\Rightarrow x^2(x^2y+1)+2y-x^2\vdots x^2y+1\Rightarrow x^2-2y\vdots x^2y+1.$ Xét $3$ trường hợp:
$+)TH1:x^2=2y\Rightarrow (x,y)=(2k^2,2k)(k\in \mathbb{Z}_+)$
$+)TH2:x^2>2y\Rightarrow x^2-2y\geq x^2y+1\Leftrightarrow (x^2+2)(y-1)\leq -3\Rightarrow y=1\Rightarrow x^4+2\vdots x^2+1\Rightarrow 3\vdots x^2+1(L)$
$+)TH3:x^2<2y\Rightarrow 2y-x^2\geq x^2y+1\Leftrightarrow (2-x^2)(y+1)\geq 3\Rightarrow x^2=1\Rightarrow x=1\Rightarrow y=2$
Vậy $\left ( x,y \right )\in \left \{ (1;2);(2k^2;2k) \right \}$
#668821 Topic ôn thi hình học vào cấp 3 chuyên
 Gửi bởi tpdtthltvp
trong 19-01-2017 - 05:56
Gửi bởi tpdtthltvp
trong 19-01-2017 - 05:56
Lời giải bài 7:
1) Ta có: $\angle FBD=\angle ECD$ và $\angle BFD=\angle DMC=\angle DEC$ suy ra $\Delta BDF\sim \Delta CDE$
Từ đó dễ dàng suy ra $\Delta DEF\sim \Delta DCB\Rightarrow \angle DFE=\angle DBC=\angle DFM\Rightarrow \overline{E,M,F}$
2) Kẻ tiếp tuyến $At$ của $(O)$ suy ra $\Rightarrow \angle tAB=\angle ADB=\angle AFE\Rightarrow AT//EF\Rightarrow EF \perp AO.$
3)
$\frac{AC}{BD}=\frac{MC}{MD};\frac{AB}{DC}=\frac{MB}{MD}\Rightarrow \frac{AC}{BD}=\frac{AB}{DC}(MB=MC)\Rightarrow \frac{AC}{AB}=\frac{DB}{DC}(1)$
Mặt khác ta lại có: $AE.AC=AB.AF(=AM.AD)\Rightarrow \frac{AC}{AB}=\frac{AF}{AE}(2)$
Từ $(1)$ và $(2)$ suy ra $\frac{AF}{AE}=\frac{DB}{EC}\Rightarrow \frac{NF}{NE}=\frac{BF}{EC}\Rightarrow \frac{NF}{BF}=\frac{NE}{EC}\Rightarrow \frac{QN}{QB}=\frac{PN}{PC}$
Theo định lí $Thales$ đảo suy ra $PQ//BC(\text{đpcm})$
Lời giải bài 8:
1) Ta có: $\angle GFA=\angle GEA \Rightarrow \angle GFB=\angle GEC.$ Mặt khác, $\angle GBF=\angle GCE$ suy ra $\Delta GBF\sim \Delta GCE\Rightarrow \Delta GNF\sim \Delta GME\Rightarrow \angle GNF=\angle GME\Rightarrow G\in (AMN)$
Gọi $P'=AK\cap (K)\Rightarrow GP' \perp AG.$ Mà tứ giác $GHEA$ nội tiếp, $\angle AEH=90^{\circ}\Rightarrow GH \perp AG.$ Do đó $P'\in GH\Rightarrow P'\equiv P\Rightarrow \text{đpcm}$
Bài toán 9: Là Bài toán 6 em đề xuất ở trên rồi thầy.
- quanghung86 và Nguyenphuctang thích
#668774 Topic ôn thi hình học vào cấp 3 chuyên
 Gửi bởi tpdtthltvp
trong 18-01-2017 - 17:47
Gửi bởi tpdtthltvp
trong 18-01-2017 - 17:47
Em xin đề xuất $2$ bài mới:
Bài toán 5 (Thi vòng 1 chuyên KHTN 2015-2016): Cho tam giác $ABC$ nhọn không cân có tâm đường tròn nội tiếp $I.$ $AI$ cắt $BC$ tại $D.$ Lấy $E,F$ lần lượt đối xứng $D$ qua $IB$ và $IC.$ $M,N,J$ lần lượt là trung điểm của $DE,DF,EF.$ Đường tròn ngoại tiếp tam giác $AEM$ cắt đường tròn ngoại tiếp tam giác $AFN$ tại $P$ khác $A.$ Chứng minh rằng $A,J,P$ thẳng hàng.
Bài toán 6 (Đề vòng 1 KHTN 2016-2017): Cho tam giác $ABC$ nội tiếp $(O)$ có A$AD$ là phân giác trong của tam giác. $AD$ cắt $(O)$ tại điểm thứ $2$ là $E.$ Gọi $M$ là trung điểm của $AD.$ $BM$ cắt $(O)$ tại điểm thứ hai $P$ khác $B.$ $EP$ cắt $AC$ tại điểm thứ hai $N.$
a) Chứng minh $N$ là trung điểm của $AC.$
b) Gọi $(EMN)$ cắt $BM$ tại $R$ khác $M.$ Chứng minh rằng $RA \perp RC.$
- quanghung86 và CaptainCuong thích
#667555 Đề thi HSG lớp 9 vòng 2 TP.Vinh
 Gửi bởi tpdtthltvp
trong 08-01-2017 - 07:39
Gửi bởi tpdtthltvp
trong 08-01-2017 - 07:39
Câu 4: (6đ)
Cho tam giác ABC cân có $\measuredangle ABC=120$ nội tiếp (O). Tiếp tuyến qua A của (O) cắt đường thẳng BC tại D. Đường thẳng DO lần lượt cắt AB,AC tại E,F. Gọi M,N lần lượt là trung điểm của AB và AC. H là giao điểm của đường thẳng AO và (O). CMR:
b) AO, MF, NE đồng quy
Mượn tạm cái nình của anh Cuongpa ![]()
Từ phần $(a)$ dễ dàng suy ra được: $\frac{ME}{MA}=\frac{1}{3}$
Mặt khác, $\frac{HA}{HO}=2,$ và $\frac{FO}{FE}=\frac{AO}{AE}=\frac{AB}{AE}=\frac{3}{2}$
Do đó: $\frac{ME}{MA}.\frac{HA}{HO}.\frac{FO}{FE}=1.$ Áp dụng định lí $Menelaus$ cho $\Delta AEO$ ta được $M,F,H$ thẳng hàng. Suy ra đpcm.
- Kagome yêu thích
#667170 $\boxed{Topic}$ ÔN THI VÀO THPT CHUYÊN TOÁN NĂM HỌC...
 Gửi bởi tpdtthltvp
trong 05-01-2017 - 21:08
Gửi bởi tpdtthltvp
trong 05-01-2017 - 21:08
$\boxed{10}.$ GHPT: $\left\{\begin{matrix} x^4+2x^3y-2x^2y^2-12xy^3+8y^4+1=0 \\ 2x^3y+y^4=1 \end{matrix}\right.$
$\boxed{11}.$ (Bài cuối cùng của phần HPT hữu tỉ)
Giải HPT: $\left\{\begin{matrix} y^3-x^3=7 \\ x^3-y^2+x=-2 \end{matrix}\right.$
- HoangKhanh2002 yêu thích
#667148 $\boxed{Topic}$ ÔN THI VÀO THPT CHUYÊN TOÁN NĂM HỌC...
 Gửi bởi tpdtthltvp
trong 05-01-2017 - 20:08
Gửi bởi tpdtthltvp
trong 05-01-2017 - 20:08
$\boxed{8}.$ Giải hệ phương trình:
$\left\{\begin{matrix}x^2(y-z)=\frac{-5}{3} \\ y^2(z-x)=3 \\ z^2(x-y)=\frac{1}{3}. \end{matrix}\right.$
$\boxed{8}.$ Đã có ở đây ![]()
$\boxed{9}.$ Giải hệ phương trình: $\left\{\begin{matrix} y^2+x(x+1)(x+2)(x+3)=121 \\ y^2+1=x \end{matrix}\right.$
- HoangKhanh2002 yêu thích
#666817 $\boxed{Topic}$ ÔN THI VÀO THPT CHUYÊN TOÁN NĂM HỌC...
 Gửi bởi tpdtthltvp
trong 03-01-2017 - 19:00
Gửi bởi tpdtthltvp
trong 03-01-2017 - 19:00
$\boxed{7}.$ Giải hệ phương trình $\left\{\begin{matrix} x^4+5y=6 \;\;\;\ (1) \\ x^2y^2+5x=6 \end{matrix}\right.$
Trừ vế với vế $2$ phương trình được:
$(x-y)(x^3+x^2y-5)=0\Leftrightarrow \begin{bmatrix} x=y \\ x^3+x^2y=5 \end{bmatrix}$
$\bullet x=y\Rightarrow \begin{bmatrix} x=y=1 \\ x=y=-2 \end{bmatrix}$
$\bullet x^3+x^2y=5:$ Từ $(1)$ suy ra $y=\frac{6-x^4}{5}\Rightarrow x^3+\frac{6x^2-x^6}{5}=5\Leftrightarrow 5x^3+6x^2-x^6=25\Leftrightarrow 2x^6-10x^3-12x^2+50=0\Leftrightarrow (x^3-5)^2+[(x^6+8+8)-12x^2]+9=0, \text{phương trình vô nghiệm}$
Vậy $\boxed{(x,y)\in \left \{ (1;1);(-2;-2) \right \}}$
- HoangKhanh2002 và ToanTHPTHT thích
- Diễn đàn Toán học
- → Đang xem trang cá nhân: Likes: tpdtthltvp



 Tìm kiếm
Tìm kiếm