Nguyen Dinh Hoang

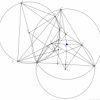
Lời giải bài 1 của mình:

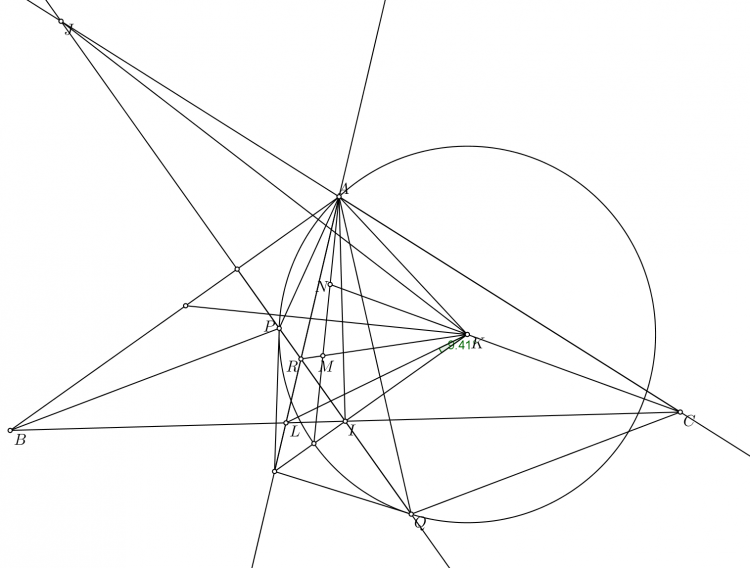
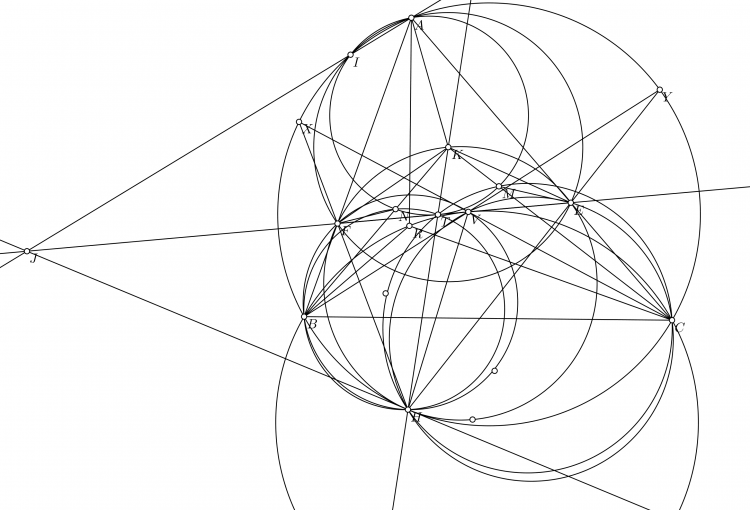
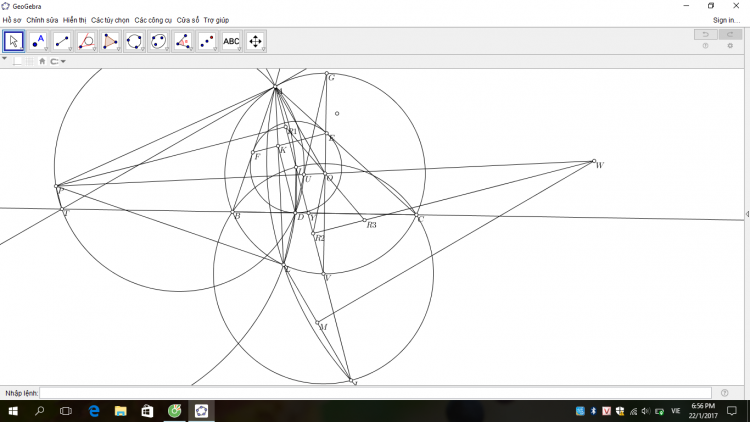
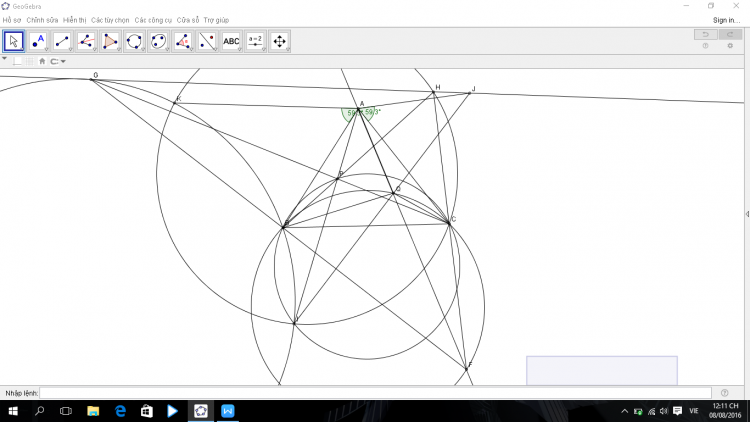
Gọi $S$, $T$ thứ tự là giao của $IC$, $IB$ với $(O)$. $X$ là trung điểm $ST$. 

Áp dụng định lý com bướm ta có $X, I, K$ thẳng hàng và $I$ là trung điểm $SK$. Gọi $Y$ là trung điểm $AX$ theo định lý Thales ta có $M$ là trung điểm $YJ$. 

Ta có $\angle AIM = 2\angle AXM = 2\angle MXY= 2(90^{\circ}-\angle MIX)$. Nên $AYIN$ nội tiếp dẫn đến $MY.MN= MA.MI$ hay $MA.MA= MJ.MN$ nên $AM$ là tiếp tuyến của $(AJN)$ hay ta chỉ cần chứng minh $AJIH$ nội tiếp. Đúng vì khi lấy đối xứng trục của $AJIH$ qua trục $AI$ thì trở thành $(AIN)$. Ta có $DPCM$ 

1 cách khác cho bài 1: 

Bổ đề: Cho $ABC$ nội tiếp $(O)$, 1 đường tròn $(K)$ bất kì qua $B, C$ cắt $AB, AC$ tại $E, F$, $P$ là giao 2 đường chéo, $Q$ là tâm của $(KEF)$. Khi đó $P, Q, O$ thẳng hàng.

Trở lại bài toán:

Gọi $G$ là giao của $FC, EB$. Ta chỉ cần chứng minh $P, G, O$ thẳng hàng.

Ta có $\angle PEF= 90^{\circ} - \angle A- \angle FEB$, $\angle OCF = \angle FCE - 90^{\circ} - \angle B$. Nên $\angle OCF = \angle JEF$. Nên $JE$ và $OC$ cắt nhau trên $(K)$ tại $U$ tương tự có $V$. Áp dụng định lý $Pasal$ cho bộ $FUVECB$ ta có $P, G, O$ thẳng hàng. $dpcm$

Lời giải của em:

Bổ đề: Cho tam giác $ABC$, $AP$, $AQ$ là 2 tia đẳng giác trong góc $BAC$. $BP$ cắt $AQ$ tại $X$, $BQ$ cắt $CP$ tại $Y$. Thì $AX$, $AY$ đẳng giác trong $BAC$. (C/m ở trước ).

Gọi $L$ là giao của $AR$ với $BC$, $J$ là giao của $AC$ với $PQ$. Ta chỉ cần chứng minh $KM$, $KN$ đẳng giác trong $AKI$. Áp dụng bổ đề ta cần chứng minh $KJ$, $KL$ đẳng giác trong $AKI$ mặt khác ta lại có $\measuredangle AIL = \measuredangle KIQ$ nên $IL$, $IQ$ đẳng giác trong $AIK$ nên ta chứng minh $L$ và $J$ là 2 điểm đẳng giác trong tam giác $AKI$ 

Ta chứng minh $\measuredangle RAI = \measuredangle KAC$. Ta có $\measuredangle KAC = \measuredangle IAC - \measuredangle IAK = \measuredangle IAB - \measuredangle KAI = \measuredangle BAI - \measuredangle BAR = \measuredangle RAI$. Ta có $DPCM$$

Lời giải: 

+,$V$ là giao của phân giác ngoài góc $A$ với $BC$. Ta chứng minh đoạn $AR$ cắt $(O)$ tại $X$ thì tiếp tuyến tại $X$ của $I$ đi qua $V$

Theo tính chất song song ta dễ có $ANDM$ nội tiếp, Gọi $Y$ là tâm của $ANDM$.  $AVDI$ nội tiếp nên ta cần chứng minh $X$ nằm trên $(AID)$ là đủ. Gọi $T$ là giao của $ID$ với $AV$. Sử dụng chùm tâm $V$ chiếu lên $ID$ ta có $(TI,RD) = -1$ mà $\measuredangle IAT = 90$ nên $AI$ là tia phân giác $\measuredangle DAR$ (1). $W$ là giao của $AI$ với $(I)$ $S$ là giao của $AR$ với $(I)$ do (1) nên $WD = WS$.$L$ là giao của $ID$ với $(I)$. Ta có $\measuredangle LXR = \measuredangle LXS = 90^{\circ} - 2\measuredangle WXD = 90^{\circ} - \measuredangle DIW= \measuredangle VTI$. Lại gọi $X'$ là giao của $(AID)$ với $(I)$ theo tc hàng điều hòa ta có tiếp tuyến tại $X'$ của $(I)$ đi qua $V$. Ta có $\measuredangle LX'R = \measuredangle LXV - \measuredangle XDV - \measuredangle DIW = 90^{\circ} - \measuredangle DIW = \measuredangle VTD$ Nên $X$ trùng $X'$ ta có $dpcm$.

+, Ta chứng minh $Y$ nằm trên $(AID)$ thật vậy ta có 2 tam giác $ANF$ và $DFJ$ đồng dạng (G.G) nên $\frac{NF}{FA} = \frac{FJ}{JD}$  thiết lập đẳng thức tương tự chú ý $JE = JF$ nên $NF = ME$ từ đó $(FDE)$ đi qua điểm chính giữa cung lớn $EF của $(I)$ hay $(FDE)$ đi qua $W$.

Nên $\measuredangle AYD = 2 \measuredangle AWD= 2 \measuredangle IWD = 180 - \measuredangle AVD$. Nên $(AID)$ đi qua $Y$.

Vậy tóm lại ta chỉ cần chứng minh $X, Y, W$ thẳng hàng là OK!. Thật vậy ta có $\measuredangle LXW = 90^{\circ} - \frac{1}{2}.\measuredangle DIW$. Mà $\measuredangle LXY = \measuredangle LXV - \measuredangle YXV = \measuredangle XDV + \measuredangle XDL - \measuredangle XDV - \measuredangle YVD = 90^{\circ} - \frac{1}{2}. \measuredangle DIW$. Nên ta có $X, Y, W$ thẳng hàng. Vậy ta có $dpcm$ 

Bài này khá dễ lời giải của em: Kí hiệu $R$ là trực tâm $ABC$ thay vì $H$

Gọi $V$ là điểm tiếp xúc của $EF$ với $HBC$ ta chứng minh $KEF$ tiếp xúc $(O)$ thật vậy $CV$ cắt $(O)$ tại $X$ tương tự có $Y$ áp dụng định lý $Pascal$ đảo ta có $XF$, $YE$ cắt nhau tại 1 điểm nằm trên $(O)$ là $H$. Do $EF$ tiếp xúc $HBC$ nên dễ có $BFVH$ nội tiếp tương tự ta có $VECH$ nội tiếp nên ta có$\measuredangle FHE = \measuredangle FBV + \measuredangle VCE = \measuredangle AFE + \measuredangle AEF + 180 - \measuredangle BVC = 180 -2 \measuredangle A = \measuredangle FKE$ nên $HFKE$ nội tiếp. Gọi $Hx$ là tiếp tuyến của $HEF$ ta có $\measuredangle xHB = \measuredangle xHF - \measuredangle FBH = \measuredangle FEH - \measuredangle FBH = \measuredangle BCH$ nên $Hx$ cũng là tiếp tuyến của $HEF$ ta có $KEF$ tiếp xúc $(O)$.

Gọi $T$ là giao của $EF$ với $KH$ ta có $KT.KH$ $=$ $KE.KE$ tính chất của điểm chính giữa cung nên. Xét nghịch đảo trong đường tròn $(K)$ thì $AEF$ đi qua $T$ và $AEF$, $(O)$, $(K)$ đồng trục. 

Áp dụng định lý tâm đẳng phương cho 3 đường tròn $(O)$, $(AFE)$, $(KEF)$ ta có $EF$, tiếp tuyến tại $H$ của $(O)$ và $IA$ đồng quy tại $J$, trong đó $I$ là giao của $(K)$ với $(O)$  

Ta chứng minh $JT$ $=$ $JH$ điều này hiển nhiên vì$\measuredangle JHT = \measuredangle JHF + \measuredangle FHT = \measuredangle THE + \measuredangle TEH = \measuredangle JTH$ nên $JT = JH$. Lại có $JI.JA= JH^{2} = JT^{2}$ nên $(AMN)$ tiếp xúc $EF$. Ta có $dpcm$

1 Lời giải thuần túy khác cho bài 143

 

Bổ đề: Cho tam giác $ABC$, trực tâm $H$, đường cao $AD$,$BE$, $CF$. $M$, $N$ lần lượt là điểm $Lemoine$ của các tam giác $BFD$, $CDE$. $I$ là trung điểm $BC$. Khi đó $MN$ vuông góc $AI$

Chứng minh:

Gọi $Q$ là giao của $EF$ và $BC$. $S$ là giao của $QH$ với $BFD$ tương tự gọi $T$. Ta có $QH$ vuông góc $AI$. Ta chứng minh $S$, $M$, $D$ thẳng hàng. Thật vậy ta có $\measuredangle MDB = \measuredangle IAC$ do đồng dạng mà $\measuredangle SDB = \measuredangle QHB = \measuredangle IAC$ nên $S$, $M$, $D$ thẳng hàng. Tương tự ta có $D,N,T$ thẳng hàng và do $DBS$ đồng dang $DET$ và $DBM$ đồng dạng $DEN$ nên $MN // ST$  nên $MN$ vuông góc $AI$

Trở lại bài toán.

Gọi $X, Y, Z$ thứ tự là điểm $Lemoine$ của $AEF$, $BCF$, $CDE$ ta có kết quả sau $XL$ vuông góc $BC$ nên Áp dụng tính chất hàng điểm vuông góc ta có $X(LYZx)$ mà Xx là đường qua $X$ và song song $YZ$ chuyển thành $A(BCIy)$ trong đó $Ay$ là đường qua $A$ song song $BC$ hàng này điều hòa nên ta có $dpcm$

anh đánh nhầm sorry em

Lời giải :
Gọi $P$ là trung điểm $SD$, $AP$ cắt $BC$ tại $R$
Ta có $TD^{2}$ $=$ $TS. TL$ nên $RP. RA = RD^{2}$ theo hệ thức $Newton$ ta có $RD^{2}= RB. RC$ nên ta có $P$ nằm trên $(O)$ áp dụng tính chất đường trung bình ta có $dpcm$

Lời giải: 

Gọi $V$ là điểm chính giữa cung $BC$ nhỏ của $(O)$

Ta chứng minh $\measuredangle DLV$ $=$ $90^{\circ}$: $EF$ cắt $BC$ tại $Z$ thì $\measuredangle ZKD = 90$ mà $(ZD,BC) = 90$ nên $LD$ là đi qua điểm chính giữa cung $BC$ lớn của $(O)$ nên $\measuredangle DLV$ $= 90$

+, Chứng minh $P$ là tâm của $AIDL$$ do $DI$ $//$ $OV$ nên  \measuredangle DIV = \measuredangle IVO= \measuredangle ALD$ nên $AIDL$ nội tiếp. Gọi $U$ là giao của trung trực $AL$ với $DL$ ta có $\measuredangle UPT = 90 - \measuredangle DGO = \measuredangle UDC$ ($G$ là điểm chính giữa cung $BC$ lớn của $(O)$ nên $PTDU$ nội tiếp. Lại có $\measuredangle AUP = \measuredangle PUL = 180 - \measuredangle PTD = \measuredangle AYT= \measuredangle TAY = \measuredangle PTA$ nên $PTDUA$ nội tiếp nên $P$ thuộc trung trực $AD$ mà $P$ thuộc trung trực $AL$ nên $P$ là tâm của $AIDL$ Gọi $W$ là điểm đối xứng của $P$ qua $(O)$ theo tính chất đường trung bình thì ta cần chứng minh $W$ là tâm của $ALJ$ 

Thật vậy ta có: Gọi $R1$, $R2$ thứ tự là trung điểm $AI$, $AJ$ thì xét phép vị tự tâm $A$ tỉ số 2 ta có $OR1$ $=$ $OR2$. Ta chứng minh $WR2$ vuông góc $AJ$ hay $WR2$ $//$ $PR1$. Gọi $R3$ là đối xứng của $R1$ qua $(O)$ ta có $R2R3$ vuông góc $AI$ mà 2 tg $OR3W$ $=$ $OR1P$ nên $WR3$ $//$ $PR1$ nên $WR2$ $//$ $PR1$ hay ta có $dpcm$

Lời giải:
Ta có $A$, $L$, $M$, $P$ , $K$ cùng thuộc đường tròn đường kính $AP$. Gọi $(AP)$ cắt $(O)$ tại $S$. Ta lại có $\angle BMH = \angle MAH = \angle MAP$$\angle BMH = \angle MAH = \angle MAP$ nên $(AP)$ tiếp xúc $BC$ Nên $AS$ $//$ $BC$. Ta có $SLB$ đồng dạng $SKC$ nên $\frac{SL}{SK} = \frac{BL}{KC}$. Nên ta có $ARQ$ đồng dạng $SLK$ đồng dạng $ACB$ nên $BRQC$ nội tiếp. Gọi $X$, $Y$ lần lượt là trung điểm $AR$, $AQ$. $(I)$ $=$ $(ARQ)$ Ta có $X$, $L$ đối xứng nhau qua trung điểm $AB$, $Y$, $K$ đối xứng nhau qua trung điểm $AC$ Nên $I$, $O$, $P$ thẳng hàng và $O$ là trung điểm $IP$. $J$ là giao của $AO$ với $RQ$. ta sẽ chứng minh $(AJM)$ tiếp xúc $MO$ tức $(AJM)$ có tâm ngoại tiếp nằm trên $BC$. Gọi tiếp tuyến tại $A$ của $(AMS)$ cắt $BC$ tại $V$. $AV$ cắt $(O)$ tại $G$. Ta lại có $KL$ cắt $BC$ tại $E$ thì $S$ là điểm $Miquel$ của tứ giác toàn phần $LKBCAE$ nên $AG$, $SE$ đối xứng nhau qua trung trực $CB$. Biến đổi góc ta có $G$ là điểm $Miquel$ của tứ giác toàn phần $XYCBAV$ Nên $XY$ đi qua $V$. Vậy ta có $V$ là giao của 2 tiếp tuyến tại $A$ và $M$ của $(AMS)$ và $XY$ là trung trực của $AJ$ nên $V$ là tâm của $(AJM)$. Tóm lại ta có $(AJM)$ tiếp xúc $MO$. Gọi $F$ là giao của $RQ$ với $BC$ ta có $FJOM$ nội tiếp $\angle JMO = \angle JFO = \angle MAO$. Nên $FO$ vuông góc $AM$. Tức $N$ là trực tâm $AOF$ nên $ON$ vuông góc $AF$. $T$ là giao của $AF$ với $(O)$ ta có $T$ là điểm $Miquel$ của tư giác toàn phần $RQCBAF$ nên $OI$ vuông góc $AF$. Vậy $I$, $N$, $O$, $P$ thẳng hàng. Ta kết thúc chứng minh.

Một bài toán mới của em dựa théo cấu trúc của Thầy Hùng mình đã post ở đây http://diendantoanho...a-2-đường-tròn/

Trong bài kiểm tra trường hè miền Bắc và trong chuyên mục mỗi tuần 1 bài toán tuần 2 tháng 8 của thầy Hùng có 2 bài toán cấu hình khá giống nhau, mình có 1 mở rộng là:

 Cho tam giác $ABC$ nội tiếp $(O)$, $D$ là 1 điểm bất kì trên $(O)$. $G$ là đối xứng của $D$ qua $BC$. $BG$ cắt $AC$ tại $F$, $CG$ cắt $AB$ tại $E$. $AG$ cắt lại $(O)$ tại $V$. $AI$ là đường kính của $(O)$. $AI$ cắt trung trực $EF$ tại $K$. $AK$ cắt lại $(O)$ tại $L$. Chứng minh rằng đường qua $K$ vuông góc $AV$, đường qua $G$ vuông góc $AL$, và $LV$ cắt nhau tại  điểm và đường tròn đi qua  điểm đó tiếp xúc với $(O)$.

 P/s: Nếu có trùng lặp ở đâu mong mọi người thứ lỗi>

Lời giải:

Trong bài này ta có 1 kết quả cơ bản sau: đường thẳng đi qua $H$ vuông góc với 1 cạnh thì đi qua trung điểm cạnh đói diện.

Gọi $M$, $N$ là trung điểm $BC$, $AD$. Ta dễ dàng có $JLNM$ nội tiếp nên $HO$ là đối trung của $JHL$ nên $HO$ cắt $JL$ tại $K$ thì $\frac{JK}{KL}= \frac{HJ^{2}}{HL^{2}}$. Mặt khác theo bổ đề $ERIQ$ đảo ta có $JL$ cắt $IK$ tại $S$ thỏa mãn $\frac{JS}{SL} = \frac{BI}{IA}$. Biến đổi theo các tam giác đồng dạng ta dễ có $S$ trùng $K$ ta có $DPCM$

Lời giải: Gọi $E$, $F$ lần lượt là chân đường cao hạ từ $B$, $C$ xuống các cạch đối diện. Ta có $MP$ đi qua trung điểm $EF$, $MP$ vuông góc $EF$. Nên $MP$ đi qua tâm tam giác $DEF$. $D$ là chân đường cao hạ từ $A$. Áp dụng kết quả cơ bản về đường thẳng $Euler$ của tam giác có 3 đỉnh là 3 tâm bàng tiếp $H, I, G, O$ thẳng hàng. Việc tính toán không quá khó!

Cho tam giác $ABC$, $P$, $Q$ là 2 điểm liên hợp đẳng giác. $AQ$ cắt $(BQC)$ tại $F$. $AP$ cắt $(BPC)$ tại $I$. $FB$ cắt $PC$ tại $G$ tương tự ta có $H$. $IQ$ cắt $GH$ tại $J$. $(GBI)$ cắt $(ICH)$ tại $K$. Chứng minh rằng $AK$, $AJ$ đẳng giác trong góc $BAC$

​Nguồn: ​Mở rộng của mình từ 1 bài toán của thầy Trần Quang Hùng