Bài Hình Đề thi chọn HSG Hải Phòng bảng chuyên.
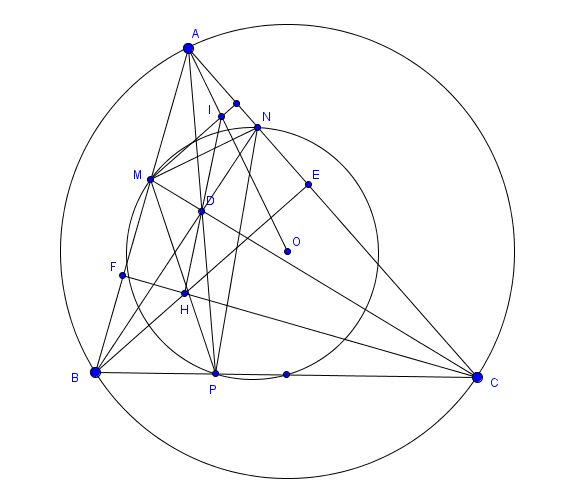
Cho tam giác nhọn $ABC$, $(AB<AC)$ nội tiếp $(O)$. Hai đường cao $BE,CF$ cắt nhau tại $H$. Một điểm $M$ di chuyển trên đoạn thẳng $AB$. Đường thẳng $d$ đi qua $M$ vuông gọc với $AC$ cắt $AO$ tại $I$; $IH$ cắt $CM$ tại $D$; $BD$ cắt $AC$ tại $N$; $AD$ cắt $BC$ tại $P$. Gọi $X$ là trung điểm của $BC$. CHứng minh rằng $MPXN$ nội tiếp.
- yeutoan2001 yêu thích


 Tìm kiếm
Tìm kiếm Bí mật
Bí mật