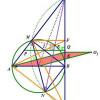
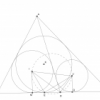
làm sao tam giác HO1M đồng dạng với tam giác CO2H được ạ.
Câu 3c. $O_{1}H$ và $O_{2}H$ là 2 tia phân giác của hai góc kề bù => $O_{1}H$ vuông góc với $O_{2}H$ .
Có $\Delta HO_{1}M đồng dạng với \Delta CO_{2}H(g.g)$ => $\frac{O_{1}H}{O_{2}H}=\frac{MH}{CH}=\frac{MB}{MC}=>\Delta O_{1}HO_{2} đồng dạng với \Delta BMC$ => $\frac{S_{O_{1}HO_{2}}}{S_{BMC}}=(\frac{O_{2}H}{CM})^{2}$ Mà $\frac{O_{2}H}{CM}=\sqrt{2}\frac{CH+MH-CM}{CM}\leq \sqrt{2}(\frac{\sqrt{2(MH^{2}+CH^{2})}-CM}{CM}=\sqrt{2}(\sqrt{2}-1)$ => $S_{O_{1}HO_{2}}\leq S_{BMC}2(\sqrt{2}-1)^{2}$ Mà $S_{BMC}=MH.\frac{BC}{2}=MH.R\leq R^{2}$. => $S_{O_{1}HO_{2}}\leq 2R^{2}(\sqrt{2}-1)^{2}$. Dấu "=" <=> M chính giữa cung BC


 Tìm kiếm
Tìm kiếm Bí mật
Bí mật