minhrongcon2000
Tìm kiếm
Nam
Trong chủ đề: VMF's Marathon Hình học Olympic
25-02-2017 - 15:47
Lời giải bài 173:
Mình xin đề xuất một cách giải không mấy sơ cấp cho bài này:
VMF.png 95.32K
46 Số lần tải
Bài toán có thể được viết lại như sau: Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ có $AB$ cắt $CD$ tại $E$, $AD$ cắt $BC$ tại $F$ và $AC$ cắt $BD$ tại $I$. Gọi $P$ là giao điểm thứ hai của đường tròn $(AEF)$ và $(O)$. $PI$ cắt $(O)$ tại điểm thứ hai là $Q$. Chứng minh rằng $C$, $Q$, $F$, $E$ cùng thuộc 1 đường tròn.
Chứng minh:
Gọi $R$ là giao điểm của $AP$ và $CQ$.
Ta có $EF$ chính là đường đối cực của $I$ qua $(O)$.
Mặt khác, do $AP$ cắt $CQ$ tại $R$ và $AC$ cắt $PQ$ tại $I$ nên ta có $R$ nằm trên đường đối cực của $I$ qua $(O)$, hay nói cách khác $AP$, $EF$, $CQ$ cùng đồng qui tại 1 điểm.
Do đó, ta có được $\overline{RF}.\overline{RE}=\overline{RA}.\overline{RP}=\overline{RQ}.\overline{RC}\Rightarrow$ tứ giác $CQFE$ nội tiếp nên ta có điều phải chứng minh.$\square$
Trong chủ đề: Đường tròn ngoại tiếp tam giác IJD đi qua một điểm cố định
24-12-2016 - 19:41
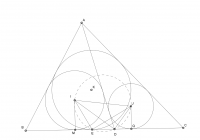
Cho tam giác ABC nhọn. Một điểm D thay đổi trên BC. Gọi I,J lần lượt là tâm đường tròn nội tiếp tam giác ABD và ACD.
a) Chứng minh rằng đường tròn ngoại tiếp tam giác IJD luôn đi qua một điểm cố định
a.png 162.14K
51 Số lần tải
Ta dễ chứng minh được các đẳng thức sau đây:
$MB=\frac{AB+BD-AD}{2}$
$BE=\frac{BC+AB-AC}{2}$
$DQ=\frac{DA+DC-AC}{2}$.
Ta có được: $ME=BE-BM=\frac{BC+AB-AC}{2}-\frac{AB+BD-AD}{2}=\frac{DC+DA-AC}{2}=DQ$.
Mặt khác, ta cũng có $\Delta IMD\sim\Delta DQJ\Rightarrow \frac{IM}{DQ}=\frac{MD}{JQ}$. Từ đây, ta có $\Delta IME\sim\Delta EQJ$, do đó $\widehat{IEJ}=90^{o}$. Do đó, ta có điều phải chứng minh.
