minhrongcon2000

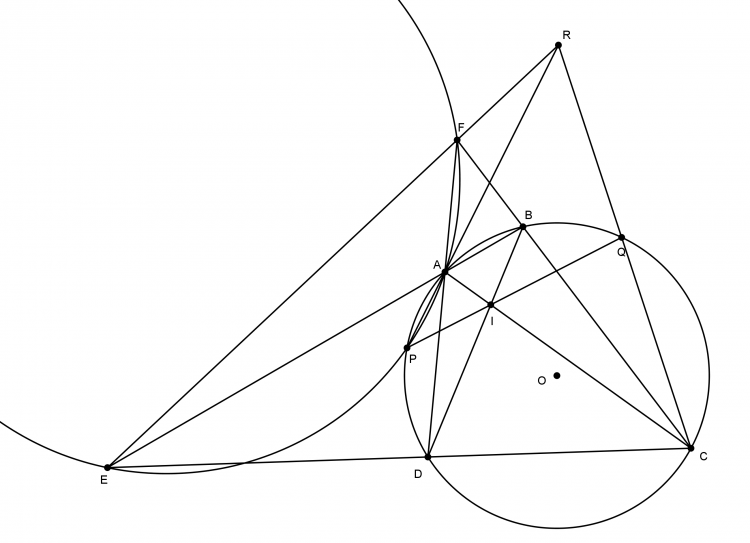
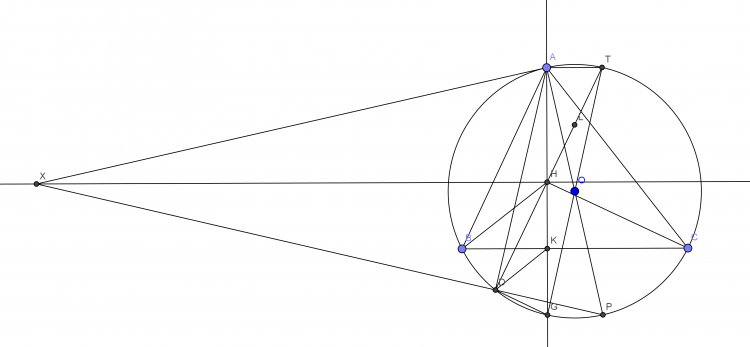
Bài toán 174. Cho $\Delta ABC$ có 1 điểm $D$ bất kì thuộc đường thẳng $BC$ sao cho $D$ và $B$ nằm khác phía so với $C$. Gọi $I$ và $I_1$ l ần lượt là tâm nội tiếp $\Delta ABC$ và $\Delta ACD$. Chứng minh rằng trục đẳng phương của $(I)$ và $(I')$ đi qua 1 điểm cố định khi $D$ thay đổi.

Lời giải bài 173: 

Mình xin đề xuất một cách giải không mấy sơ cấp cho bài này:

 

Bài toán có thể được viết lại như sau: Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ có $AB$ cắt $CD$ tại $E$, $AD$ cắt $BC$ tại $F$ và $AC$ cắt $BD$ tại $I$. Gọi $P$ là giao điểm thứ hai của đường tròn $(AEF)$ và $(O)$. $PI$ cắt $(O)$ tại điểm thứ hai là $Q$. Chứng minh rằng $C$, $Q$, $F$, $E$ cùng thuộc 1 đường tròn.

Chứng minh:

Gọi $R$ là giao điểm của $AP$ và $CQ$. 

Ta có $EF$ chính là đường đối cực của $I$ qua $(O)$. 

Mặt khác, do $AP$ cắt $CQ$ tại $R$ và $AC$ cắt $PQ$ tại $I$ nên ta có $R$ nằm trên đường đối cực của $I$ qua $(O)$, hay nói cách khác $AP$, $EF$, $CQ$ cùng đồng qui tại 1 điểm.

Do đó, ta có được $\overline{RF}.\overline{RE}=\overline{RA}.\overline{RP}=\overline{RQ}.\overline{RC}\Rightarrow$ tứ giác $CQFE$ nội tiếp nên ta có điều phải chứng minh.$\square$

 

Cho tam giác ABC nhọn. Một điểm D thay đổi trên BC. Gọi I,J lần lượt là tâm đường tròn nội tiếp tam giác ABD và ACD.

a) Chứng minh rằng đường tròn ngoại tiếp tam giác IJD luôn đi qua một điểm cố định

 

Ta dễ chứng minh được các đẳng thức sau đây:  

$MB=\frac{AB+BD-AD}{2}$

$BE=\frac{BC+AB-AC}{2}$

$DQ=\frac{DA+DC-AC}{2}$.

Ta có được: $ME=BE-BM=\frac{BC+AB-AC}{2}-\frac{AB+BD-AD}{2}=\frac{DC+DA-AC}{2}=DQ$.

Mặt khác, ta cũng có $\Delta IMD\sim\Delta DQJ\Rightarrow \frac{IM}{DQ}=\frac{MD}{JQ}$. Từ đây, ta có $\Delta IME\sim\Delta EQJ$, do đó $\widehat{IEJ}=90^{o}$. Do đó, ta có điều phải chứng minh.

Cho em hỏi một chút! Nếu mà đề bài của thầy Hùng cho như vậy thì hai tam giác $PCE$ và $PBF$ phải cân tại $B$ và $C$ chứ nhỉ? Như vậy thì hình vẽ sẽ khác............

Bài phương trình hàm có vẻ đánh lừa người làm nhỉ? Giả sử tồn tại hàm $f$ thỏa đề.

Thay $x=y=1$, $f(2)-2=2f(1)$.

Thay $x=1$, $y=2$, $f(3)=f(2)+f(1)+3$

Thay $x=y=2$, $f(4)=2f(2)+5$

Thay $x=3$, $y=1$, $f(4)=f(3)+f(1)+4$.

Từ đây, ta có $2f(2)+5=f(3)+f(1)+4\Leftrightarrow 4f(1)+7=f(2)+2f(1)+7\Leftrightarrow f(2)=2f(1)\Leftrightarrow 2f(1)+2=2f(1)$ (Vô lí). Do đó, không tồn tại hàm thỏa đề.

Bài 3 là một bài quen thuộc! 

Câu a chỉ cần vẽ đường kính và chứng mình $A$, $H$, $K$, $G$ thẳng hàng là xong. 

Câu b thì chứng minh $AHDX$ nội tiếp là ok

Cho y=f(x), y=g(x) cùng là hàm chẵn trên D. Xét tính chẵn lẻ của từng hàm số sau

a. y= f(x) + g(x)

b. y= f(x) - g(x)

c. y= f(x).g(x)

d. y= $\frac{f(x)}{g(x)}$ (g(x) khác 0) với mọi x thuộc D

Câu trả lời là tất cả đều chẵn hết! Lấy ví dụ một câu rồi bạn làm tương tự nhé!

a) Đặt $y=h(x)$. Như vậy $h(-x)=f(-x)+g(-x)=f(x)+g(x)=h(x)$ nên $y$ chẵn

Cho dãy x_n  : x₁ = $\sqrt{2}$ , x_n+1  = $\sqrt{2 + x_{n}}$ . Chứng minh rằng {x_n} là dãy hội tụ và tìm giới hạn.

Bài này có nhiều cách làm! Mình xin trình bày một trong số cách làm đó!

Xét hàm $f(x)=\sqrt{2+x}\Rightarrow f'(x)=\frac{1}{2\sqrt{2+x}}>0$. Do đó, $f$ đồng biến. Mặt khác, $u_1<u_2$ nên $f(u_1)<f(u_2)\Rightarrow u_2<u_3$. Tương tự như thế ta có $(u_n)$ tăng. Bằng quy nạp, ta có $u_{n}<2\forall n$. Theo định lí $Bolzano-Weistrass$, dãy $(u_n)$ hội tụ. Giả sử $(u_n)\rightarrow a$. Khi đó, ta có phương trình $a=\sqrt{2+a}\Leftrightarrow a=2$. Do đó, $\lim u_n=2$

 

Cho tập $A={0,1,2,3,4,5,6}$. Có bao nhiêu số gồm 4 chữ số thuộc$A$ mà có ít nhất hai chữ số giống nhau.

Bài này đơn giản thôi bạn! 

Bước 1: Ta đếm số các số có 6 chữ số. Có tất cả $6*7*7*7*7*7=100842$ số thỏa điều này.

Bước 2: Ta đếm số các chữ số có 6 chữ số khác nhau đôi một. Có tất cả $6*6*5*4*3*2=4320$ số như vậy.

Vậy có tất cả $100842-4320=96522$ số thỏa đề!

Câu 4 chính là đề IMO 2010!

nhưng mình nghĩ số $0\leq k\leq n$.

Ah! Mình ghi sai kí hiệu! Thành thật xin lỗi bạn

Bạn có thể giải thích tại sao khi chọn 3 vị trí cho số 1 thì có $C_{3}^{7}$ cách không chỗ đấy mình chưa hiểu lắm.

Tại vì lúc này bạn sẽ loại bỏ được vị trí $a_1$ và chỉ còn lại 7 vị trí cho 3 số 1

Tìm tất cả các hàm $f:\mathbb{R}\rightarrow \mathbb{R}$ thoả mãn điều kiện:

 

$f(x-f(y))=3f(x)-2x-f(y) \forall x,y\in \mathbb{R}$

Ta đặt $g(x)=f(x)-x$.

Ta sẽ có $g(x-f(y))=3g(x)$. Do đó, $g(x-3f(y))=27g(x)$. 

Mặt khác, $f(x-f(y))-3f(x)=-2x-f(y)$ nên $f$ toàn ánh và $\forall x\in\mathbb{R},\exists u,v\in\mathbb{R}:x=f(u)-3f(v)$.

Nói một cách khác, do $x-y\in\mathbb{R}$ nên $\exists u,v: x-y=f(u)-3f(v)\Rightarrow x-f(u)=y-3f(v)\Rightarrow 3g(x)=g(x-f(u))=g(y-3f(v))=27g(y)\Rightarrow g(x)=9g(y)$. Hoán đổi x,y ta cũng có $g(y)=9g(x)$ nên $g(x)=g(y)\forall x,y\in\mathbb{R}$ nên $g$ là hàm hằng. Từ đó ta có $f(x)=x+c$ với $c$ là hằng số thực. Thử lại, ta có $f(x)=x$ thỏa đề.

Với các chữ số 0,1,2,3,4,5 ta có thể lập được bao nhiêu số gồm 8 chữ số trong đó chữ số 1 có mặt 3 lần, mỗi chữ số khác có mặt đúng 1 lần?. Bao nhiêu số gồm 4 chữ số và trong đó có mặt chữ số 5

Về vế thứ nhất: "Có bao nhiêu số có 8 chữ số mà chữ số 1 có mặt 3 lần và các số khác có mặt đúng 1 lần?"
Gọi số cần tìm là $\overline{a_{1}a_{2}...a_{8}}$.
Trường hợp 1: $a_{1}=1$.
Ta chọn hai vị trí còn lại cho số 1, có $C_{7}^{2}$ cách.
Các vị trí còn lại có $5!$ cách. Vậy sẽ có tất cả là $5!*C_{7}^{2}$ số thỏa đề.
Trường hợp 2: $a_{1}\neq 1$.
Ta chọn 3 vị trí cho số $1$, có $C_{7}^{3}$ cách.
Các vị trí còn lại (để ý nếu $a_{1}=0$ thì sẽ không phải là một số có $8$ chữ số), có $4*4*3*2*1$ cách.
Vậy có tất cả $5!*C_{7}^{2}+4*4*3*2*C_{7}^{3}=5880$ số thỏa đề.

Về vế thứ hai: "Bao nhiêu số gồm 4 chữ số trong đó có mặt chữ số 5.
Ta có thể lập được tất cả $5*6*6*6$ số có 4 chữ số.
Mặt khác, ta có thể lập được $4*5*5*5$ số 4 chữ số mà không có mặt chữ số 5.
Vậy có tất cả $5*6*6*6-4*5*5*5=580$ số thỏa đề..

Bài 1:

Xét hàm số $f(x)=\frac{x+a}{1+ax}$.

Khi đó, $f'(x)=\frac{1+ax-a(x+a)}{(1+ax)^{2}}=\frac{1-a^{2}}{(1+ax)^{2}}<0$ $\forall \frac{1}{2}<a<1$.

Mặt khác, $x_{1}=\frac{a_{1}+x_{0}}{1+a_{1}x_{0}}=\frac{a_{1}+a_{0}}{1+a_{1}a_{0}}>a_{0}=x_{0}$ nên $(x_{n})$ là dãy tăng.

Và bằng qui nạp, ta chứng minh được $x_{n}<1$ $\forall n \geqslant 0$ nên dãy $(x_{n})$ hội tụ. Vì $(a_{n})$ là dãy bị chặn nên có thể trích ra một dãy con $(a_{n_{k}})$ hội tụ. Nếu ta xét dãy con $(x_{n_{k}})$ thì $\lim_{k\rightarrow \infty}x_{n_{k}}=\lim_{n\rightarrow\infty}x_{n}$. Giả sử $(x_{n_{k}})\rightarrow x$ và $(a_{n_{k}})\rightarrow a$. Ta sẽ có phương trình 

$x=\frac{x+a}{1+ax}\Leftrightarrow x=1$ (do $a>0$ và $x>0$). Như vậy $\lim_{n\rightarrow \infty}x_{n}=1$