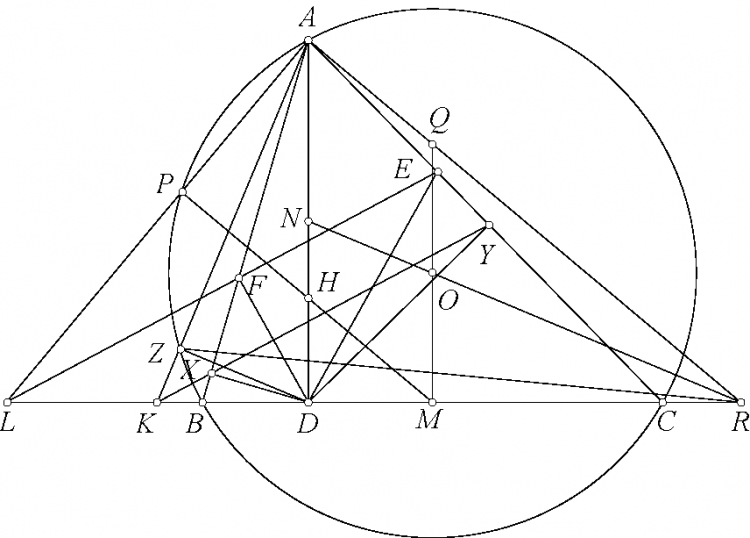
Do đó tồn tại đường tròn $(O')$ tiếp túc trong cả hai đường tròn $(O)$ và $(J)$.
$AJ$ cắt $ON$ tại $I$. $O'I$ cắt $AN$ tại $P$. Gọi $\alpha_1, \alpha_2$ là đường tròn tâm $I$ tiếp xúc $AB, AC$ và $NL, NK$. Theo định lý $Monge-D'Alambert$, ta có $A$ là tâm vị tự ngoài của $\alpha_1$ và $(J)$, $N$ là tâm vị tự ngoài của $(J)$ và $(O')$, từ đó suy ra $P$ là tâm vị tự ngoài của $\alpha_1$ và $(O')$. Tương tự $P$ là tâm vị tự ngoài của $\alpha_2$ và $(O')$. Suy ra $\alpha_1 \equiv \alpha_2$. Như vậy $AKNL$ ngoại tiếp.
- Zaraki, canhhoang30011999, ecchi123 và 3 người khác yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam
















 Gửi bởi
Gửi bởi