doremon01

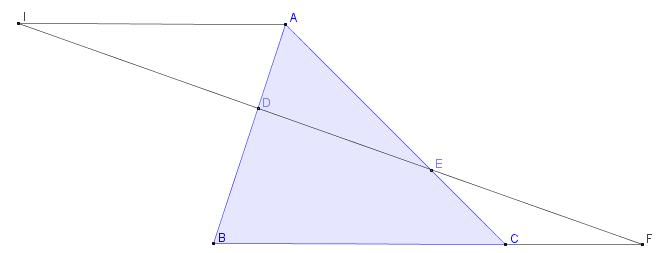
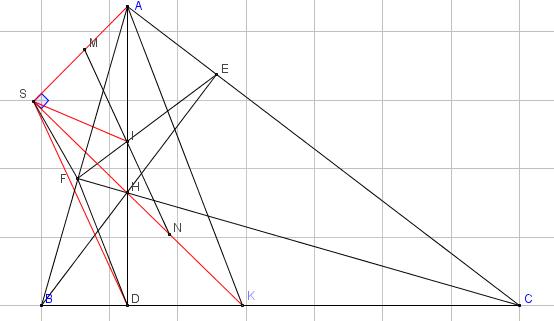
Cố định A trên đường tròn lớn

Gọi $R_1;R_2$ là bán kính 2 đường tròn ($R_1<R_2$)

Dựng đoạn thẳng h có độ dài bằng $\frac{\sqrt{9R_1^2-R_2^2}}{2\sqrt2}$

Vẽ đường tròn $(O;h)$

Kẻ tiếp tuyến Ax từ A đến $(O;h)$

$Ax$ cắt $(O_1);(O_2)$ lần lượt tại B,C,D

ĐK: $x\geq 0;y\geq 0$

Ta có: $x+y\geq \frac{(\sqrt{x}+\sqrt{y})^2}{2}=2;x^2+y^2\geq \frac{(x+y)^2}{2}\geq 2\Rightarrow x+y+x^2+y^2\geq 4$

Mặt khác: $8=2^{x^{2}+y}+2^{x+y^{2}}\geq 2\sqrt{2^{x^{2}+y}.2^{x+y^{2}}}=2\sqrt{2^{x^2+y^2+x+y}}\geq 2\sqrt{2^4}=8$

Dấu đẳng thức xảy ra $\Leftrightarrow x=y=1$

Thử lại, ta thấy $(x;y)=(1;1)$ là nghiệm duy nhất của phương trình

6) $\sqrt[4]{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2$ ĐK: $x \geq 1$

Đặt $\sqrt[4]{x-\sqrt{x^2-1}}=a\geq 0; \sqrt{x+\sqrt{x^2-1}}=b\geq 0\Rightarrow \left\{\begin{matrix} a^2b=1\\a+b=2 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=2-a\\ a^2(2-a)=1 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=2-a\\ a^3-2a^2+1=0 \end{matrix}\right.\Leftrightarrow \begin{bmatrix} (a;b)=(1;1)\: \: \: \: \: \: \: (1)\\ (a;b)=(\frac{1+\sqrt5}{2};\frac{3-\sqrt5}{2})\, \, \, \, (2) \end{bmatrix}$

Giải (1) ta được $x=1$

Giải (2) ta thấy phương trình vô nghiệm với  $x \geq 1$

Vậy $x=1$ là nghiệm duy nhất của phương trình

HM cắt AD tại E

Áp dụng định lí Menelaus vào $\Delta BAH$ với cát tuyến CIK ta có:

$\frac{AK}{KB}.\frac{CB}{CH}.\frac{IH}{IA}=1\Leftrightarrow \frac{IH}{IA}=\frac{KB.CH}{AK.CB}$

$\Delta HAE$ có: 

$\frac{HI}{IA}.\frac{DA}{DE}.\frac{ME}{MH}=\frac{KB.CH}{AK.CB}.\frac{DA}{DE}.\frac{ME}{MH}=1$ nên D,M,I thẳng hàng

Chứng minh định lí Pappus:   http://vuontoanblog....-mysticum3.html

Bạn có thể tham khảo cách chứng minh định lí Menelaus [khá đơn giản]:

Xét $\Delta ABC$ có một đường thẳng cắt 3 cạnh AB,AC,BC ( hoặc đường thẳng chứa cạnh) lần lượt tại D,E,F . Qua A vẽ đường thẳng song song BC cắt DE tại I

$\frac{AD}{DB}.\frac{FB}{FC}.\frac{EC}{EA}=\frac{AI}{FB}.\frac{FB}{FC}.\frac{CF}{AI}=1$

Mở rộng bài toán trên: Cho tam giác ABC vuông tại A. E ϵ BC. E ≠ B, C. Gọi H, F lần lượt là hình chiếu của E xuống AB, AC. Gọi K là giao điểm CH, BF. CM: Đường thẳng EK luôn đi qua 1 điểm cố định khi E di chuyển trên BC.

Vẽ hình chữ nhật ABDC

FE cắt BD tại I; BC cắt DF tại M

$\Delta BHE \sim \Delta EFC (g-g) \Rightarrow \frac{EF}{HB}=\frac{FC}{HE}\Leftrightarrow EF.HE=HB.FC$

Áp dụng định lí Menelaus vào $\Delta BAF$ với cát tuyến CKH ta có: 

$\frac{KB}{KF}.\frac{CF}{CA}.\frac{HA}{HB}=1\Leftrightarrow \frac{FK}{KB}=\frac{CF.HA}{CA.HB}$

$\Delta FBD$ có: 

$\frac{DM}{MF}.\frac{KF}{KB}.\frac{IB}{ID}=\frac{BD}{FC}.\frac{CF.HA}{CA.HB}.\frac{IB}{ID}=\frac{EF}{HB}.\frac{HE}{FC}=1$

Theo định lí Ceva thì DK, BM,FI đồng quy tại E
Vậy D,E,K thẳng hàng hay EK luôn đi qua điểm D cố định

Ta sẽ chứng minh $\frac{HA.HB}{BC.AC}+\frac{HB.HC}{AC.AB}+\frac{HC.HA}{AB.BC}=1$

$\Delta AHE\sim \Delta ACD(g-g)\Rightarrow \frac {HA}{AC}=\frac{AE}{AD}\Leftrightarrow \frac{HA.HB}{BC.AC}=\frac{AE.HB}{AD.BC}=\frac{S_{AHB}}{S_{ABC}}$

Chứng minh tương tự: 

$\frac{HB.HC}{AC.AB}=\frac{S_{BHC}}{S_{ABC}}$

$\frac{HC.HA}{AB.BC}=\frac{S_{AHC}}{S_{ABC}}$

Cộng từng vế các đẳng thức trên ta có: $\frac{HA.HB}{BC.AC}+\frac{HB.HC}{AC.AB}+\frac{HC.HA}{AB.BC}=1$

Ta có: $(\frac{HA}{BC}+\frac{HB}{AC}+\frac{HC}{AB})^2 \geq 3.\frac{HA.HB}{BC.AC}+\frac{HB.HC}{AC.AB}+\frac{HC.HA}{AB.BC}=3$

 (do $ (a+b+c)^2 \geq 3(ab+bc+ca)$)

Vậy $\frac{HA}{BC}+\frac{HB}{AC}+\frac{HC}{AB} \geq \sqrt3$

Tứ giác $AEHF$ có: $\angle EAF=\angle HEA=\angle HFA=90^o$ nên tứ giác $HEAF$ là hình chữ nhật $\Rightarrow HE=AF$

$\Delta BHE$ và $\Delta BCA$ có: $\angle EBH: chung; \angle BEH=\angle BAC=90^o$ nên $\Delta BHE \sim \Delta BCA(g-g) \Rightarrow \frac{HE}{BE}=\frac{AC}{AB}\Leftrightarrow AC.BE=HE.AB \Leftrightarrow \frac{AC,BE}{2}=\frac{AF.AB}{2}\Leftrightarrow S_{CBE}=S_{ABF}\Leftrightarrow S_{AEMF}+S_{BME}=S_{CMB}+S_{BME}\Leftrightarrow S_{AEMF}=S_{CMB}$ 

**Bài toán vẫn đúng nếu điểm H di động trên BC**

BFEC nội tiếp $\Rightarrow \angle HFE=\angle HBC$

HFBD nội tiếp $\Rightarrow \angle HFD=\angle HBD$

Vì $\angle HFD=\angle HFI (cmt) $ nên FH là đường phân giác trong  $\Delta IFD$ 

Mà $FA \perp FH; A \epsilon ID$  nên FA là đường phân giác ngoài $\Delta FID$

Do đó: $\frac{HD}{HI}=\frac{AD}{AI}(=\frac{FD}{FI})$ (1)

Qua I kẻ đường thẳng song song SD cắt SA;AH lần lượt tại M,N

IN//SD $\Rightarrow \frac{HD}{HI}=\frac{SD}{IN}$ (2)

IM//SD $\Rightarrow \frac{AD}{AI}=\frac{SD}{IM}$ (3)

Từ (1),(2),(3) ta có: IM=IN

$\Delta SMN$ có $\angle MSN=90^o$ và I là trung điểm MN nên $IS=IM=IN$

$IS=IN \Rightarrow \angle ISN=\angle INS$ (4)

IN//SD $\Rightarrow \angle INS=\angle DSN$ (5)

Từ (4) và (5) ta có: $\angle ISN=\angle DSN$ nên SH là tia phân giác của $\angle DSI $

Áp dụng định lí Menelaus vào $\Delta AIB'$ với cát tuyến MA'B ta có: 

$\frac{B'M}{MA}.\frac{AB}{BI}.\frac{A'I}{A'B'}=1\Leftrightarrow \frac{B'M}{MA}.2.\frac{A'I}{A'B'}=1$ (1) 

Áp dụng định lí Menelaus vào $\Delta B'IB$ với cát tuyến CA'C ta có:

$\frac{B'C}{CB}.\frac{AB}{AI}.\frac{A'I}{A'B'}=1\Leftrightarrow \frac{B'C}{CB}.2.\frac{A'I}{A'B'}=1$ (2)

Từ (1) và (2) ta có: $ \frac{B'M}{MA}=\frac{B'C}{CB} \Leftrightarrow MC//AB$

Vậy M luôn nằm trên đường thẳng qua C và song song với AB

Vẽ hình vuông ACBD

Ta sẽ chứng minh $DE \perp HF$

EH cắt DC tại M, FE cắt BD tại N,DE cắt HF tại I

Ta có: DM=BH;DN=EF

$\Delta DME$ và $\Delta EHF$ có: 

$ \angle DME=\angle HEF=90^o$

$EH=DM(=BH); EM=EF$ 

$\Rightarrow \Delta DME=\Delta HEF (c-g-c) \Rightarrow \angle DEM=\angle EFH \Leftrightarrow \angle HEI=\angle HFE \Leftrightarrow \Delta HEI \sim \Delta HFE (g-g)\Rightarrow DE \perp HF$ $\Rightarrow $ DE là đường cao của $\Delta DHF$ (1)

Mặt khác: $\Delta DBH$ và $\Delta BAF$ có: $DB=BA;\angle DBH=\angle BAF=90^o;BH=AF$ nên $\Delta DBH=\Delta BAF(c-g-c) \Rightarrow \angle ABF=\angle BDH\Rightarrow \angle ABF+\angle BHD=\angle BDH+\angle BHD=90^o\rightarrow BF\perp HD\Rightarrow$FB là đường cao của $\Delta DHF$ (2)

Chứng minh tương tự ta được : HC là đường cao $\Delta DHF$(3)

Từ (1); (2);(3) ta có: DE;BF;HC đồng quy tại trực tâm $\Delta HFD$ 

Mà $K=BF\cap CH$ nên DE đi qua I

Vậy EK luôn đi qua D là điểm cố định

Bài toán vẫn đúng nếu $\Delta ABC$ vuông tại A

Gọi I là giao điểm 2 đường chéo của hình bình hành thứ 1

K là giao điểm 2 đường chéo của hình bình hành thứ 2

Đường thẳng đi qua IK là đường thẳng cần dựng

b) Tương tự câu a, ta cũng chứng minh được $BF\perp CE$

CM cắt DA tại H

Ta có: $\frac{DH}{DC}=\frac{DH}{CB}=\frac{MD}{MB}=\frac{MF\sqrt{2}}{ME\sqrt{2}}=\frac{MF}{ME}=\frac{AE}{AF}\Rightarrow \Delta AEF\sim \Delta DHC(c-g-c)\rightarrow \angle FHC=\angle AEF\Rightarrow \angle HFE+\angle FHC=\angle HFE+\angle AEF=90^o\rightarrow CM \perp EF$

$\Delta CFE$ có CM,FB,ED là các đường cao nên DE, BF, CM đồng quy tại trực tâm $\Delta CFE$

IP cắt CD tại E

Áp dụng định lí Menelaus vào $\Delta ABC$ với cát tuyến INM ta có: 

$\frac{AM}{MB}.\frac{IB}{IC}.\frac{NC}{NA}=1\Leftrightarrow \frac{IB}{IC}=\frac{NA}{NC}=\frac{PB}{PD}$

Áp dụng định lí Menelaus vào $\Delta DBC$ với cát tuyến PEI ta có:

$\frac{ED}{EC}.\frac{IC}{IB}.\frac{PB}{PD}=1\Leftrightarrow \frac{ED}{EC}.\frac{IC}{IB}.\frac{IB}{IC}=1\Leftrightarrow ED=DC$

Vậy IP luôn đi qua trung điểm E của DC