Lời giải ( cách hơi dở):
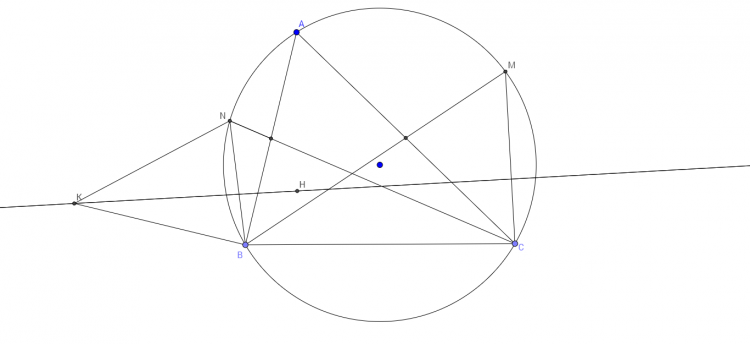
Gọi $K$ là giao điểm $BM,CF$.
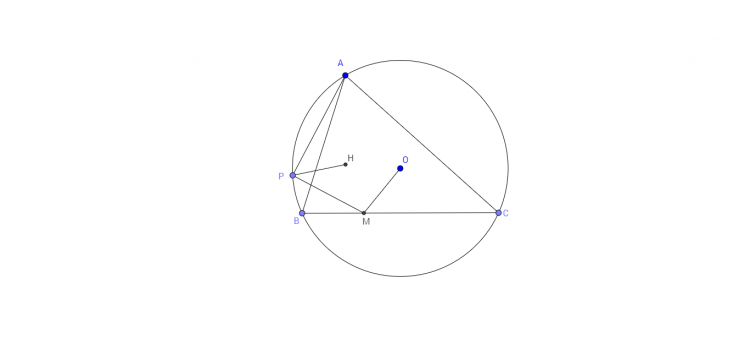
Xét cực và đối cực đối với $(CH)$.
Dễ thấy $BM$ là đường đối cực của $A$, đi qua $K$ nên đường đối cực của $K$ đi qua $A$. Mà $AB$ vuông góc $CF$ và tâm $(CH)$ thuộc $CF$ nên $AB$ là đường đối cực của $K$.Suy ra đường đối cực của $B$ chính là $AT$ sẽ đi qua $K$.(ĐPCM)
- quantv2006 yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam













 Gửi bởi
Gửi bởi