QuangDuong12011998

Lời giải của mình.

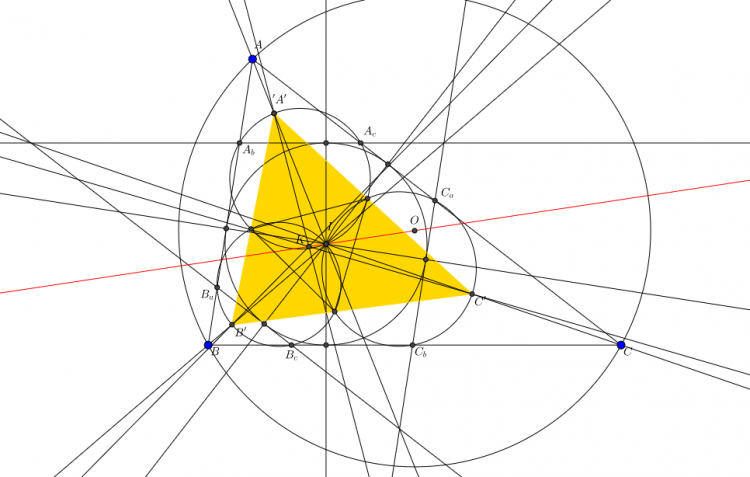
Hai điểm isodynamic là giao điểm của 3 đường tròn Apollonius của $\triangle ABC$ dựng trên $BC$, $CA$, $AB$, lần lượt với tỉ số $\dfrac{AB}{AC}$, $\dfrac{BC}{BA}$, $\dfrac{CA}{CB}$

Hiển nhiên là $\dfrac{KB}{KC}=\dfrac{AB}{AC}$ nên $A$, $K$, $P$, $Q$ thuộc đường tròn Apollonius trên $BC$, tỉ số $\dfrac{AB}{AC}$.

Đường tròn Apollonius thì trực giao với đường tròn ngoại tiếp, do vậy $R$ cũng là nghịch đảo của $K$ qua $(O)$.

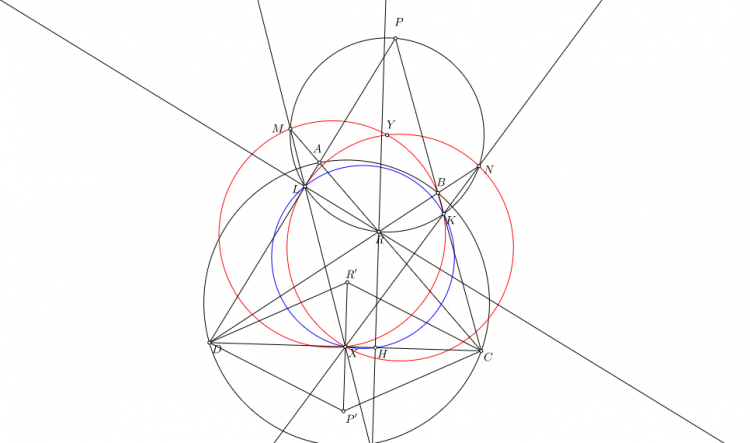
Gọi $T$ là giao điểm hai tiếp tuyến tại $B$, $C$ của $(O)$. $M$ là trung điểm $BC$, $I$ là trung điểm $OT$ và $J$ là đối xứng của $O$ qua $M$.

Xét phép nghịch đảo đường tròn $(O)$, kí hiệu $I^{R^2}_O$

\[I^{R^2}_O:A, R\mapsto A, K\Rightarrow I^{R^2}_O: AR\rightarrow (OAK)\]

$A$ và $K$ đối xứng qua $BC$, $O$ và $J$ đối xứng qua $BC$ nên $(OAK)$ luôn đi qua $J$ cố định.

Mà $AR$ là ảnh của $(OAK)$ qua phép nghịch đảo $(O)$ nên $AR$ đi qua nghịch đảo của $J$ qua $(O)$, tức là $AR$ đi qua $I$.

$BC$, $(O)$ cố định nên $T$ cố định, kéo theo  $I$ cố định.

Vậy $AR$ luôn đi qua tâm của $(OBC)$.

Lời giải bài 38.

Bài 38 được Telv Cohl đề nghị trong marathon hình học trên AoPS http://www.artofprob...1198358p5979646

và được bạn Trịnh Huy Vũ tổng quát lên cho hai điểm đẳng giác tại đây http://artofproblems...onjugate_points

Mình post chứng minh bằng tọa độ barycentric trong post của Trịnh Huy Vũ.

Theo mình đây là một bài toán rất đẹp, không chỉ ở hình vẽ mà ngay cả biểu thức tọa độ. Tính toán khá nhẹ nhàng vì tọa độ các điểm khá gọn. Quá trình làm mất khoảng 1 tiếng 

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 8\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 9\\ \hline QuangDuong12011998 & 5\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Lời giải bài 35 bởi Telv Cohl

http://artofproblems..._conjugate_pair

Với bài này thì mình không dùng góc định hướng như mọi khi nữa, dựa theo hình vẽ trên của Bảo, khi mà đáy $AD$ bé hơn đáy $BC$.

Thực ra bài này chỉ cần chứng minh $(DEF)$ trực giao $(O)$.

$AB$ cắt $CD$ tại $T$. $DE$ cắt $OA$ tại $K$. $EF$ cắt $AD$ tại $J$.

Áp dụng định lý Thales

\[\dfrac{\overline{KA}}{\overline{KO}}=\dfrac{\overline{EJ}}{\overline{EX}}=\dfrac{\overline{EA}}{\overline{EB}}\]

theo định lý Thales đảo thì $DE$ song song $OB$.

Từ các đường thẳng song song này mà ta rút ra tính chất : $EA$ là phân giác $\angle DEF$.

Tiếp theo ta chỉ ra $A$ là tâm đường tròn nội tiếp $\triangle DEF$.  Chú ý là nếu $I$ là tâm nội tiếp $\triangle ABC$ thì $\angle BIC=90^o+\angle BAC$

\[\angle DEF=2\angle AEF=2\angle OAD\]

\[\angle DAF=180^o-\angle CAD=180^o-\angle ACB\Rightarrow 2\angle DAF=360^o-2\angle CAD=360^o-\angle AOD=180^o+2\angle OAD\]

Vậy $A$ là tâm nội tiếp $\triangle DEF$.

Mà $T$ thuộc phân giác $EA$, $TA=TD$ nên cũng có $TA=TD=TF$ và $T$ thuộc $(DEF)$.

\[\angle ODO'=\angle ODA+\angle O'DA=\angle ODA+\angle O'DE-\angle ADE=\angle ODA+90^o-\angle DTE-(\angle EAF-90^o)\]

\[=\angle ODA+90^o-\angle DTA+90^o-(180^o-\angle BAC)=\angle ODA+180^o-\angle DTA-180^o+\angle BAC\]

\[=\angle ODA+\angle BAC-\angle DTA=90^o-\dfrac{\angle AOD}{2}+\angle BAC-(\angle BAC-\angle ACD)\]

\[=90^o+\angle ACD-\dfrac{\angle AOD}{2}=90^o\]

Điều này nghĩa là $(O)$ và $(DEF)$ trực giao.

Nghịch đảo đường tròn $(DEF)$ thì $PQ$ thành $(O'PQ)$ còn $(O)$ vẫn là $(O)$. Mà $(O)$ tiếp xúc $PQ$ nên $(O)$ tiếp xúc $(O'PQ)$.

______________________________________

P.S: Không phải là chuyện gì to tát khi không ai thích tính toán trong hình học cả nhưng có buồn khi thấy phương pháp tọa độ bị phân biệt đối xử. Mình thỉnh thoảng sẽ vẫn tham gia giải bài, tuy nhiên đề nghị Bảo xóa tên mình khỏi bảng điểm đi.

Đề nghị bài tiếp theo

$\boxed{\text{Bài toán 35}}$(Quan sát) Cho $A$, $B$, $C$, $P$. $PA$, $PB$, $PC$ cắt $(PBC)$, $(PCA)$, $(PAB)$ tại $D$, $E$, $F$. $I$, $I_a$, $I_b$, $I_c$ là tâm nội tiếp, bàng tiếp $\triangle ABC$. $P^*$ đẳng giác với $P$ trong $\triangle BAC$. Khi đó $(P^*I_aD)$, $(P^*I_bE)$, $(P^*I_cF)$, $(I_aEF)$, $(I_bFD)$, $(I_cDE)$ đồng quy.

______________________________________

Bài 35 đã được post trong một bài viết của mình trên blog. Tuy có lời giải ngắn(không sơ cấp) nhưng nó lại được xem là hệ quả trực tiếp của kết quả không sơ cấp lắm. Post lên đây hi vọng các bạn quan tâm và có lời giải sơ cấp.

Một bài toán gần giống đã được thầy Hùng đăng tại http://artofproblems...1174125p5654683

Mình lấy bài này là hệ quả từ cái khác nên cũng không biết lời giải sơ cấp của nó có khó không.

Trong trường hợp vấn đề quá khó thì mình khuyến khích các bạn đăng ý tưởng để cùng nhau giải quyết.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 6\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 8\\ \hline QuangDuong12011998 & 4\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Đành trâu bò vậy.

Kí hiệu $a$, $b$, $c$ là độ dài $BC$, $CA$, $AB$. $p,R,r$ là nửa chu vi, bán kính đường tròn ngoại tiếp, nội tiếp $\triangle ABC$.

$S_A=\dfrac{b^2+c^2-a^2}{2}$, $S_B=\dfrac{c^2+a^2-b^2}{2}$, $S_C=\dfrac{a^2+b^2-c^2}{2}$

các công thức sử dụng xem tại https://blogcuaquang...oa-o-ti-cu.html

\[BA_1=\dfrac{IB}{\cos\dfrac{B}{2}}=\dfrac{2r}{2\sin\dfrac{B}{2}\cos\frac{B}{2}}=\dfrac{2r}{\sin B}=\dfrac{4Rr}{CA}=\dfrac{2ca}{a+b+c}=\dfrac{ca}{p}\]

\[\Rightarrow CA_1=a-BA_1=a-\dfrac{2ca}{a+b+c}=\dfrac{a(p-c)}{p}\]

\[\Rightarrow \dfrac{\overline{A_1B}}{\overline{A_1C}}=-\dfrac{c}{p-c}\]

Tương tự

\[\dfrac{\overline{A_2B}}{\overline{A_2C}}=-\dfrac{p-b}{p}\]

Tọa độ tỉ cự $A_1=(0:p-c:c)$, $A_2=(0:b:p-b)$. $AA_1$, $AA_2$ cắt $(ABC)$ tại $A_3$, $A_4$ thì

$A_3=\Big{(}-\dfrac{a^2(p-c)}{b^2-c^2+pc}: p-c:c\Big{)}$, $A_4=\Big{(}-\dfrac{a^2(p-b)}{c^2-b^2+pb}:b: p-b\Big{)}$. Từ đó lập phương trình đường thẳng $A_3A_4$

\[x\cdot p(p-a)+y\cdot a^2(p-b)\Big{(}\frac{c}{c^2-b^2+pb}-\frac{p-c}{b^2-c^2+pc}\Big{)}+z\cdot a^2(p-c)\Big{(}\dfrac{b}{b^2-c^2+pc}-\dfrac{p-b}{c^2-b^2+pb}\Big{)}=0\]

\[\Leftrightarrow x\cdot p(p-a)+y\cdot a^2(p-b)\dfrac{pb(b+c-p)}{(c^2-b^2+pb)(b^2-c^2+pc)}+z\cdot a^2(p-c)\dfrac{pc(b+c-p)}{(c^2-b^2+pb)(b^2-c^2+pc)}\]

$A_3A_4$ cắt $BC$ tại $A_0$ thì $A_0=(0:-c(p-c):b(p-b))$

Tương tự $B_0=(c(p-c):0:-a(p-a))$, $C_0=(-b(p-b):a(p-a):0)$

Do vậy $A_0$, $B_0$, $C_0$ thẳng hàng và đường thẳng chứa chúng có phương trình

\[a(p-a)x+b(p-b)y+c(p-c)z=0\]

$I=(a:b:c)$, $H=(S_BS_C:S_CS_A:S_AS_B)$. $IH$ có phương trình

\[x\cdot S_A(p-a)(b-c)+y\cdot S_B(p-b)(c-a)+z\cdot S_C(p-c)(a-b)=0\]

Điểm vô cùng của $\overline{A_0.B_0,C_0}$ có tọa độ $((b-c)(p-a):(c-a)(p-b):(a-b)(p-c))$ là điểm $X_{522}$ trong danh sách ETC http://faculty.evans...opedia/ETC.html và điểm vô cùng của $IH$ chính là điểm $X_{515}$. Và cũng theo danh sách ETC(phần về $X_{515}$) thì có viết "$X_{515}$=orthopoint of $X_{522}$". Nghĩa của orthopoint xem tại http://faculty.evans...a/glossary.html : khái niệm này chỉ dùng cho 2 điểm vô cùng, giả sử gọi $P$, $Q$, nếu $P$ nằm trên họ đường thẳng có phương $\ell_P$, $Q$ nằm trên họ đường thẳng có phương $\ell_Q$ thì $P$ gọi là orthopoint của $Q$ nếu $\ell_P\perp \ell_Q$.

Vậy kết luân $IH$ vuông góc $\overline{A_0,B_0,C_0}$.

P.S: Bài của thầy Hùng đã có tại http://artofproblems...1230964p6219712 và Luis Gonzales, Telv Cohl có những lời giải khéo léo, đơn giản hơn.

Ngoài ra, nếu thay $I$ bởi điểm bất kì thì không phải lúc nào cũng đúng. Thay $I$ bởi $P$ thì $A_0$, $B_0$, $C_0$ chỉ thẳng hàng khi $P$, đẳng giác của $P$ và trọng tâm $\triangle ABC$ thẳng hàng.

Mình đề nghị bài tiếp theo

$\boxed{\text{Bài toán 32}}$(Quan sát được) Hai điểm $P$, $Q$ thỏa mãn $(PB,PC)+(QB,QC)=(PC,PA)+(QC,QA)=(PA,PB)+(QA,QB)=0$

$P_a$, $P_b$, $P_c$ đối xứng $P$ qua $BC$, $CA$, $AB$.

$Q_a$, $Q_b$, $Q_c$ đốii xứng $Q$ qua $BC$, $CA$, $AB$.

thì $(ABC)$, $(P_aP_bP_c)$, $(Q_aQ_bQ_c)$ có trục đẳng phương chung - nói cách khác là đồng trục.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 5\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 3\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Thưa thầy và các bạn, đường tròn mixtilinear có nhiều tính chất đẹp, cả mixtilinear trong lẫn ngoài.

Với cảm nhận hình học của mình, em tin có thể mở rộng được một lượng rất lớn các tính chất đẹp của đường tròn mixtilinear.

Đặc biệt là đường thẳng mà Bảo nêu trên chắc hẳn còn chứa nhiều điểm khác - tương tự đường thẳng $OI$.

Nhất định em sẽ đào sâu vấn đề này 

Xin lỗi thầy và các bạn, lời giải cho bài toán tổng quát ở trên chưa được hoàn chỉnh, hic. Do chưa chỉ ra $T,G,H,E,F$ đồng viên.

Continue:

$QQ$ là tiếp tuyến tại $Q$ của $(QBC)$

\[(CA,GH)=(PP,AB)=(PP,PB)+(PB,BA)=(CP,CB)+(BP,BA)\]

\[=(CA,CQ)+(BC,BQ)=(CA,CQ)+(CQ,QQ)=(CA,QQ)\]

$\Rightarrow$ $GH$ tiếp xúc $(QBC)$ tại $Q$.

$(TGH)$ cắt $AC$, $AB$ tại $E'$, $F'$ khác $G$, $H$. $TE'$, $TF'$ cắt $(ABC)$ tại $M$, $N$.

Bổ đề. $\triangle ABC$, $M$, $N$ thuộc $BC$ thì $(AMN)$ tiếp xúc $(ABC)$ khi và chỉ khi $AM$, $AN$ đẳng giác với góc $A$.

Chứng minh bổ đề: $O$, $I$ là tâm của $(ABC)$ và $(AMN)$, $AH$ là đường cao của $\triangle ABC$ thì đương nhiên $AH$ cũng là đường cao của $\triangle AMN$. $AH$, $AO$ đẳng giác với $\angle (AB,AC)$; $AH$, $AI$ đẳng giác với $\angle (AM,AN)$ nên $(A,O,I)$ thẳng hàng khi và chỉ khi $\angle(AB,AC)$ và $\angle (AM,AN)$ có chung phân giác - tức là $AM$, $AN$ đẳng giác.

Quay lại bài toán.

Do đã có $(TGH)$ tiếp xúc $(ABC)$ tại $T$ nên theo bổ đề: $TM$, $TY$ đẳng giác với $\angle (TA,TC)$; $TN$, $TZ$ đẳng giác với $\angle (TA,TB)$.

$\Rightarrow$ $MY$ song song $CA$, $NZ$ song song $AB$. Điều này nghĩa là $BM$, $BY$ đẳng giác với $\angle(BA,BC)$ và $CN$, $CZ$ đẳng giác với $\angle (CA,CB)$(cung chứa góc). Do đó $BM$, $CN$ đi qua $P$.

Tương tự như chứng minh $YZ$ song song $GH$ ở trên, ta có thể chỉ ra $EF$ song song $MN$.

Mà theo định lý Pascal, $E'$, $P$, $F'$ thẳng hàng. $T$ là tâm vị tự của $(TGHE'F')$ và $(ABC)$ nên

\[\dfrac{\overline{TF'}}{\overline{TN}}=\dfrac{\overline{TH}}{\overline{TZ}}=\dfrac{\overline{TG}}{\overline{TY}}=\dfrac{\overline{TE'}}{\overline{TM}}\]

theo định lý Thales đảo, $E'F'$ song song $MN$.

Như vậy $EF$, $E'F'$ đều đi qua $P$ và song song $MN$ nên kết luân $E'=E$, $F'=F$

Vậy $(EFGH)$ tiếp xúc $(ABC)$.

P.S: Tổng quát của Bảo cũng là mở rộng đường tròn mixtilinear. Sẽ đẹp hơn nếu phát biểu lại như sau: tiếp tuyến tại $P$ của $(PBC)$ cắt $AC,AB$ tại $E$, $F$; tiếp tuyến tại $Q$ của $(QBC)$ cắt $AC,AB$ tại $G$, $H$ thì $E,F,G,H$ cùng thuộc một đường tròn tiếp xúc $(ABC)$

Cặp điểm đẳng giác luôn rất thu hút. Phải đăng nhập để like cho Bảo!

Lời giải của mình.

$QB$, $QC$ cắt $(ABC)$ tại $Y$, $Z$.

$GY$ cắt $HZ$ tại $T$ thì theo định lý Pascal đảo, $T$ thuộc $(ABC)$.

Cộng góc

\[(HG,YZ)=(HG,HA)+(AB,AZ)+(ZA,ZY)=(HG,HF)+(CB,CQ)+(BA,BQ)\]

\[=(EG,EF)+(CP,CA)+(BP,BC)=(AC,PP)+(CP,CA)+(BP,BC)\]

\[=(AC,PP)+(CP,CA)+(BP,BC)=(PC,PP)+(BP,BC)=0\]

trong đó $PP$ là tiếp tuyến tại $P$ của $(PBC)$

Suy ra $GH$ song song $YZ$, theo đó, $(TGH)$ tiếp xúc $(TYZ)$ nên $(TGH)$ tiếp xúc $(ABC)$.

Mình giải thích thuật ngữ và kí hiệu trong bài toán 20.

Tứ giác toàn phần $(a,b,c,d)$ là hình phẳng tạo bởi 4 đường thẳng $a,b,c,d$ đôi một cắt nhau và không có 3 đường nào đồng quy.

Kí hiệu $P_{bc}$ là giao điểm của $b$ với $c$. Tương tự có $P_{ca}$, $P_{ab}$, $P_{da}$, $P_{db}$, $P_{dc}$.

Đường tròn Miquel của tứ giác toàn phần $(a,b,c,d)$ là đường tròn đi qua tâm đường tròn ngoại tiếp của $\triangle P_{bc}P_{db}P_{dc}$, $\triangle P_{ca}P_{dc}P_{da}$, $\triangle P_{da}P_{db}P_{ab}$, $\triangle P_{bc}P_{ca}P_{ab}$, ngoài ra nó còn đi qua điểm đồng quy của 4 đường tròn ngoại tiếp này.

Bài toán 20 là một tính chất rất đẹp của các đường tròn Miquel và lúc trước mình đã mất khá nhiều thời gian mới nhìn ra được lời giải. Bài toán này khó ở chỗ phải vẽ thêm đường phụ. Nếu xuất phát như bài toán thì không dễ dàng thấy các đường tròn có những điểm chung nào, để chứng minh đường tròn đồng quy như kiểu bài này thì cần phải tìm điểm chung của từng cặp trước, sau đó mới có thể chỉ ra chúng đồng quy.

Cuối cùng, thực sự mong muốn Bảo sửa lại điểm 2 cho mình như cũ nhé.

Giá như đã nghĩ đến từ trước :3

Mình đưa ra lời giải dùng nghịch đảo cho bài 19. Kí hiệu vẫn như trong chứng minh cũ.

Gọi $D$, $E$, $F$ là tiếp điểm của đường tròn nội tiếp với $BC$, $CA$, $AB$.

$DX$, $EY$, $FZ$ là đường kính đường tròn nội tiếp.

$(IA_bA_c)$, $(IB_cB_a)$, $(IC_aC_b)$ có đường kính $IA'$, $IB'$, $IC'$ nên giao điểm của từng cặp là hình chiếu vuông góc của $I$ lên $B'C'$, $C'A'$, $A'B'$ mà ta kí hiệu là $A_1$, $B_1$, $C_1$. Theo như chứng minh cũ của mình thì $\overrightarrow{IA'}=\dfrac{a\overrightarrow{IA}}{p}$ nên $\sum\overrightarrow{IA'}=\dfrac{1}{p}\sum a\overrightarrow{IA}=\overrightarrow{0}$ nên $I$ là trọng tâm $\triangle A'B'C'$. $K$ là điểm Lemoine của $\triangle A'B'C'$ nên $I$ và $K$ đẳng giác trong $\triangle A'B'C'$. Do đó tâm của đường tròn $(A_1B_1C_1)$ là trung điểm $IK$, ta kí hiệu là $J$. Giờ chỉ cần chứng minh $J$ thuộc $OI$ (*)

Đến đây xét phép nghịch đảo đường tròn nội tiếp $I^{r^2}_I$

\[I^{r^2}_I: A_b,A_c,B_c,B_a,C_a,C_b,A_1,B_1,C_1\mapsto A'_b,A'_c,B'_c,B'_a,C'_a,C'_b,A'_1,B'_1,C'_1\]

Và qua phép nghịch đảo này thì $A'_b$, $A'_c$, $B'_c$, $B'_a$, $C'_a$, $C'_b$ là trung điểm $XF$, $XE$, $YD$, $YF$, $ZE$, $ZD$.

$\triangle DEF$ và $\triangle A'_1B'_1C'_1$ vị tự. Ta cần tìm tâm vị tự.

$A'_1B'_1$ $||$ $DE$(đường trung bình), $\perp$ $DY$ $\Rightarrow$ $DB'_c\perp A'_1C'_b$. Hoàn toàn tương tự, $DC'_b\perp A'_1B'_c$

$\Rightarrow$ $D$ là trực tâm $\triangle A'_1B'_cC'_b$ $\Rightarrow$ $A'_1D\perp B'_cC'_b$ $\Rightarrow$ $A'_1D\perp YZ$ $\Rightarrow A'_1D\perp B'_1C'_1,EF$. Vậy tâm vị tự chính là trực tâm chung $L$ của $\triangle DEF$ và $\triangle A'_1B'_1C'_1$. Từ điều này cũng suy ra $\triangle DEF$ và $\triangle A'_1B'_1C'_1$ có chung đường thẳng Euler $OI$. Từ đó, tâm của $(A'_1B'_1C'_1)$ thuộc $OI$. (1)

Mà $A'_1,B'_1,C'_1$ là ảnh của $A_1,B_1,C_1$ qua $I^{r^2}_I$ nên tâm ngoại tiếp của $\triangle A'_1B'_1C'_1$, $\triangle A_1B_1C_1$, $I$ thẳng hàng. Tức là tâm $(A'_1B'_1C'_1)$ thuộc $IJ$. (2)

Từ (1)(2) suy ra $J$ thuộc $OI$.

Theo (*) thì $K$ thuộc $OI$.

Cách giải khác cho bài 4, dài hơn, nhưng mà phát triển một tí: gọi $R'$, $P'$ là điểm đẳng giác của $R$ với $\triangle PDC$ và $\triangle RDC$.

Bằng cách sử dụng các đường đẳng giác, cộng góc đơn thuần ta thu được:

\[(R'C,R'D)=(PC,PD)-(RC,RD)\qquad  (P'C,P'D)=(RC,RD)-(PC,PD)\]

Điều này dẫn tới việc $P'$, $R'$ đối xứng nhau qua $BC$. Chú ý thêm từ các đường đẳng giác và $ABCD$ nôi tiếp thì $(DR',DC)=(DP,DR)=(CR,CP)=(CD, CR')$ do đó $\triangle R'DC$ cân tại $R'$, kéo theo $R'X$ vuông góc $CD$. $R'$ là đẳng giác của $R$ trong $\triangle PAD$ nên $X$ thuộc đường tròn pedal của $R$ với $\triangle PAD$. $RH\perp CD$, $H\in CD$.

Áp dụng định lý Pascal cho lục giác $PLMRNK$ thì ta thu được giao điểm của $LM$ và $KN$ nằm trên $CD$.

\[(LM,KN)=(LM,LR)+(KR,KN)+(RL,RK)=(PM,PR)+(PR,PN)+(PD,PC)=(PM,PN)+(PD,PC)=(RC,RD)+(PD,PC)\]

\[=(CR,CP)+(DP,DR)=(HR,HK)+(HL,HR)=(HL,HK)\]

Điều này nghĩa là giao của $LM$, $KN$ nằm trên đường tròn pedal của $R$ với $\triangle PCD$ và nằm trên $CD$. Hoàn toàn tương tự, ta chứng minh được $LM$, $KN$ cắt nhau trên đường tròn pedal của $P$ với $\triangle RCD$. Do đó $LM$, $KN$ đi qua $X$.

\[(XL,XN)=(XL,XK)=(LM,KN)=(RC,RD)+(PD,PC)=(CR,CP)+(DP,DR)=2(CA,CB)\]

\[(YL,YN)=2(RL,RN)=2(RL,PL)+2(PL,RN)=2(PL,RN)=2(DA,DB)=2(CA,CB)\]

Vậy có điều phải chứng minh.

Đề nghị bài tiếp theo:

$\boxed{\text{Bài toán 5}}$ (Luiz Gonzalez)  $\triangle ABC$, $P$. $PA$, $PB$, $PC$ cắt $BC,CA,AB$ tại $D,E,F$. Chứng minh trục đẳng phương của 3 cặp đường tròn sau đồng quy: $(ABE)$ và $(ACF)$, $(BCF)$ và $(BAD)$, $(CAD)$ và $(CBE)$

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline fatcat12345 & 1\\ \hline dogsteven & 2\\ \hline baopbc & 1\\ \hline QuangDuong12011998 & 1\\ \hline\end{array}$$

Ý b trong bài toán của thầy, việc 6 đường tròn đồng quy đã được đề cập tại http://gjarcmg.geome...ath-journal.ro/ 2016

Tuy nhiên việc điểm đồng quy của 6 đường tròn là đẳng giác của điểm trên lại chưa được nhắc tới, em sẽ chứng minh lại điều này như sau.

Thực ra thì cấu hình $\triangle ABC$, $P$, $Q$ đẳng giác, $PA$, $PB$, $PC$ cắt $(PBC)$, $(PCA)$, $(PAB)$ tại $X$, $Y$, $Z$, $QX$, $QY$, $QZ$ cắt $YZ$, $ZX$, $XY$ tại $U$, $V$, $W$ và cấu hình 4 điểm mà em nhắc tới ở trên là giống hệt nhau. Cho nên em sẽ chứng minh trong cấu hình 4 điểm.

Phát biểu: 4 điểm $A$, $B$, $C$, $D$. $DA$, $DB$, $DC$ cắt $BC$, $CA$, $AB$ tại $X$, $Y$, $Z$. $M_x$, $M_y$, $M_z$ là điểm Miquel của các tứ giác toàn phần $(AB,AC,DB,DC)$, $(BC,BA,DC,DA)$, $(CA,CB,DA,DB)$.

Chứng minh

Từ bài báo http://forumgeom.fau...01413index.html , bản tiếng Việt tại https://blogcuaquang...toan-chung.html thì ta có ngay $\triangle AM_yM_z$, $\triangle M_xBM_z$, $\triangle M_xM_yC$ đồng dạng cùng hướng, cũng từ điều này mà rút ra được $(AM_yM_z)$, $(BM_zM_x)$, $(CM_xM_y)$, $AM_x$, $BM_y$, $CM_z$ đồng quy tại một điểm $D'$

Cũng từ bài báo, điểm Miquel là tâm phép đồng dạng thuận nên $\triangle M_xM_zA$ và $\triangle M_xDM_y$ đồng dạng thuận, kéo theo đó là $M_xD'$, $M_xD$ đẳng giác với góc $\angle (M_xM_y,M_xM_z)$, hoàn toàn tương tự với góc $M_y$, $M_z$ của $\triangle M_xM_yM_z$ mà suy ra $D'$ và $D$ đẳng giác trong $\triangle M_xM_yM_z$. Điều này cho thấy sự tương đương của hai cấu hình =)))

Cũng từ bài báo mà $XM_x$, $YM_y$, $ZM_z$, $(XM_yM_z)$, $(YM_zM_x)$, $(ZM_xM_y)$ đồng quy tại 1 điểm $O$ $(*)$

Tiếp theo, chỉ ra $(M_xBC)$, $(M_xDA)$, $(M_yCA)$, $(M_yDB)$, $(M_zAB)$, $(M_zDC)$ đồng quy.

\[(M_xB,M_xC)=(M_xB,M_xD)+(M_xD,M_xC)=(ZB,ZD)+(YD,YC)=(AB,DC)+(DB,CA)=(AB,AC)+(DB,DC)\]

Tương tự

\[(M_yC,M_yA)=(BC,BA)+(DC,DA)\]

\[(M_zA,M_zB)=(CA,CB)+(DA,DB)\]

Từ đó $(M_xB,M_xC)+(M_yC,M_yA)+(M_zA,M_zB)=0$. Do vậy mà $(M_xBC)$, $(M_yCA)$, $(M_zAB)$ đồng quy tại 1 điểm $I$. Lúc này chỉ cần chỉ ra $(M_xDA)$ đi qua $I$ là đủ. Tiếp tục cộng góc chay

\[(IM_x,IA)=(IM_x,IC)+(IC,IA)=(BM_x,BC)+(M_yC,M_yA)=(M_xB,M_xD)+(M_xD,BC)+(BC,BA)+(DC,DA)\]

\[=(ZB,ZD)+(M_xD,BA)+(DC,DA)=(AB,DC)+(DC,DA)+(M_xD,BA)=(DM_x,BA)+(AB,AD)=(DM_x,DA)\]

Vậy $(M_xDA)$ đi qua $I$.

Bước cuối cùng, ta cần chứng minh $I$ và $O$ đẳng giác với $\triangle M_xM_yM_z$. Để chứng minh điều này mà thông qua hai đường đẳng giác, cá nhân em thấy có lẽ không khả thi, nên em đề xuất tính chất đơn giản, chứng minh bằng cộng góc và điểm trùng: $\triangle ABC$ hai điểm $P$, $Q$ đẳng giác với $\triangle ABC$ khi và chỉ khi chúng thỏa mãn hai hệ thức $(PB,PC)+(QB,QC)=(AB,AC)$, $(PC,PA)+(QC,QA)=(BC,BA)$.

Do tính đối xứng nên chỉ cần chứng minh với đỉnh $M_x$ là đủ. Áp dụng tính chất $(*)$ và chú ý $\triangle M_xM_yC$ và $\triangle M_xBM_z$ đồng dạng thuận

\[(IM_y,IM_z)=(IM_y,IA)+(IA,IM_z)=(M_yC,AC)+(AB,M_zB)=(M_yC,M_zB)+(AB,AC)\]

\[=(M_xC,M_xM_z)+(AB,AC)\]

\[(OM_y,OM_z)=(XM_y,XM_z)=(XM_y,XD) + (XD, XM_z)=(CM_y , CD) + (BM_z, BD)= (CM_y , BM_z) + (DB, DC)\]

\[=(DB,DC)+(M_xM_y,M_xB)\]

\[\Rightarrow(IM_y,IM_z)+(OM_y,OM_z)=(M_xM_y,M_xM_z)+(M_xC,M_xB)+(AB,AC)+(DB,DC)=(M_xM_y,M_xM_z)\]

Vậy $O$ và $I$ đẳng giác trong $\triangle M_xM_yM_z$.

Em xin nói thêm về bài toán tổng quát.

Nhìn hình vẽ và lời giải của Bảo trong post bên trên theo một cách khác:

$\triangle XYZ$ có $\triangle UVW$ là tam giác ceva của $Q$ với $\triangle XYZ$.

$A$ là điểm Miquel của tứ giác toàn phần tạo bởi 4 đường thẳng $(XY,XZ,QY,QZ)$

$B$ là điểm Miquel của tứ giác toàn phần tạo bởi 4 đường thẳng $(YZ,YX,QZ,QX)$

$C$ là điểm Miquel của tứ giác toàn phần tạo bởi 4 đường thẳng $(ZX,ZY,QX,QY)$.

Ở đây để tiện cho phát biểu em thay đổi chút kí hiệu :3 : 4 điểm $A$, $B$, $C$, $D$. $DA\cap BC=X$, $DB\cap CA=Y$, $DC\cap AB=Z$.

$M_x$, $M_y$, $M_z$ là điểm Miquel của các tứ giác toàn phần $(AB,AC,DB,DC)$, $(BC,BA,DC,DA)$, $(CA,CB,DA,DB)$.

Có nhiều điều hấp dẫn quanh cấu hình này:

1) $XM_x$, $YM_y$, $ZM_z$ đồng quy(là bài tổng quát ở trên), mà nó là http://artofproblems...1060982p4643389

2) $AM_x$, $BM_y$, $CM_z$ đồng quy. http://artofproblems...h282732p1526167

3) Đường tròn Miquel của 3 tứ giác toàn phần nêu trên đồng quy.

4) $(M_xDA)$, $(M_xBC)$, $(M_yDB)$, $(M_yCA)$, $(M_zDC)$, $(M_zAB)$ đồng quy tại một điểm $I$, được gọi là tâm đẳng giác của 4 điểm $A$, $B$, $C$, $D$.

Đây là điểm đáng chú ý nhất trong cấu hình 4 điểm. Gần như mọi tính chất của điểm này có trong http://www.chrisvant...a/25-qa-p4.html . Hiện chưa có bản tiếng Việt :3 em dư định sắp tới làm một tổng kết về nó :3

Rất thích các bài toán liên quan đến hai điểm đẳng giác và trong topic này thì rất ấn tượng với tổng quát của Bảo.

Phía trên thầy Hùng cũng đã đưa ra thêm bộ ba đường đồng quy trong cấu hình bài toán tổng quát.

Xin đưa ra thêm một số điều nữa, hi vọng sẽ nhận được nhiều sự quan tâm, phát triển:

1) $DX$, $EY$, $FZ$ đồng quy tại $I$.

2) Khi $D$, $E$, $F$ di chuyển trên $KA$, $KB$, $KC$ thì điểm đồng quy của $AX$, $BY$, $CZ$ và điểm $I$ lần lượt chạy trên hai đường thẳng đi qua $L$.