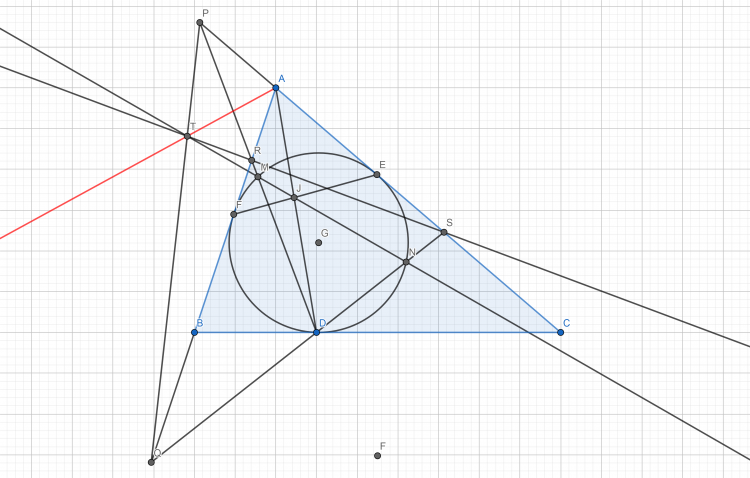
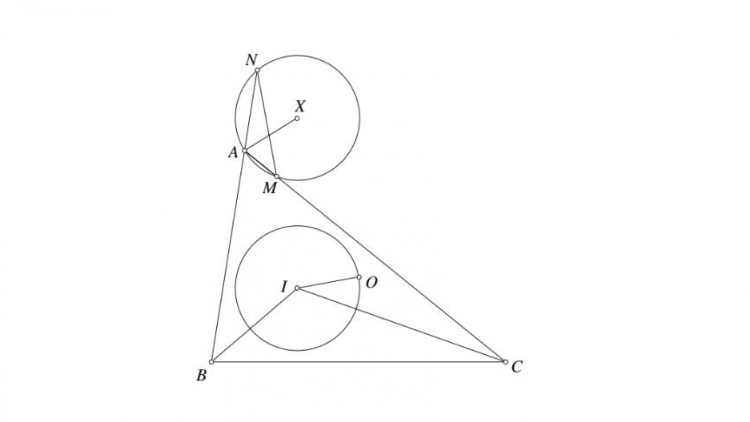
Cho tam giác $ABC$, điềm $P$ bất kỳ nằm trên đường trung trực của đoạn $BC$.Gọi $Q$ là điểm liên hợp đẳng giác của $P$. Giao của $(BPC)$ với $AB,AC$ lần lượt là $E,F$. Giao của $CE$ và $BF$ là H Chứng minh: $P,H,Q$ thẳng hàng
- Tea Coffee và DOTOANNANG thích


 Tìm kiếm
Tìm kiếm Nam
Nam














 Gửi bởi
Gửi bởi