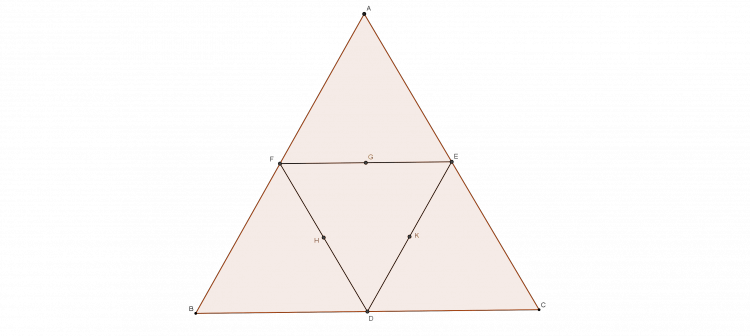
Cho tam giác ABC đường tròn nội tiếp (I) tiếp xúc BC tại D, L đối xứng với D qua I. AL cắt BC tại K. Chứng minh BK=CD
Bài trên có thể viết lại như sau:
Cho $\triangle ABC$,$D,E$ là tiếp điểm của đường tròn nội tiếp $(I)$ và bàng tiếp $(J)$ góc $A$ với $BC$.$ID\cap (I)\equiv K$. Chứng minh: $A,K,E$ thẳng hàng.
Dễ thấy $AB,AC$ là tiếp tuyến của $(I),(J)$ nên $A$ là tâm vị tự ngoài của phép vị tự hai đường tròn trên.Ta có: $E,D$ đối xứng với nhau. Do đó, 2 điểm này tương ứng là hai điểm vị tự đường tròn $(I),(J)$.Theo phép vị tự tâm $A$ thì $A,K,E$ thẳng hàng.
- tritanngo99 và AGFDFM thích



 Tìm kiếm
Tìm kiếm
 Nam
Nam











 Gửi bởi
Gửi bởi