manhtuan00

em nghĩ có thể mở rộng bài 2 như sau (chứng minh bằng vị tự quay)

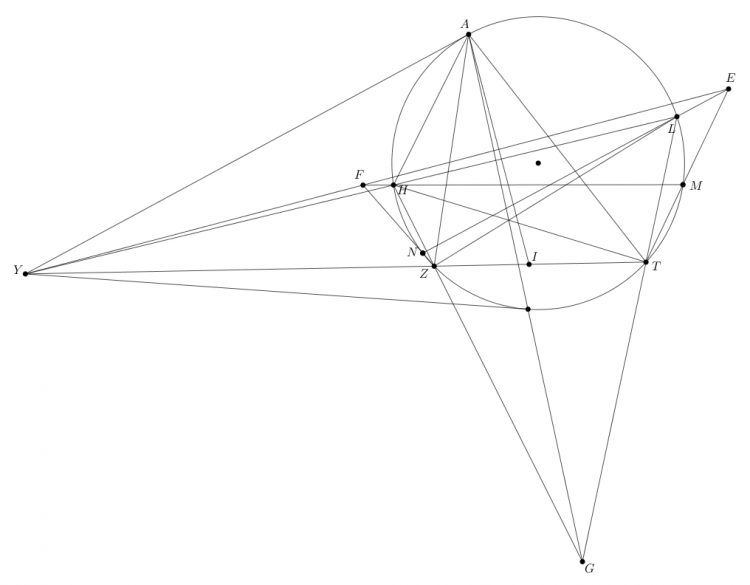
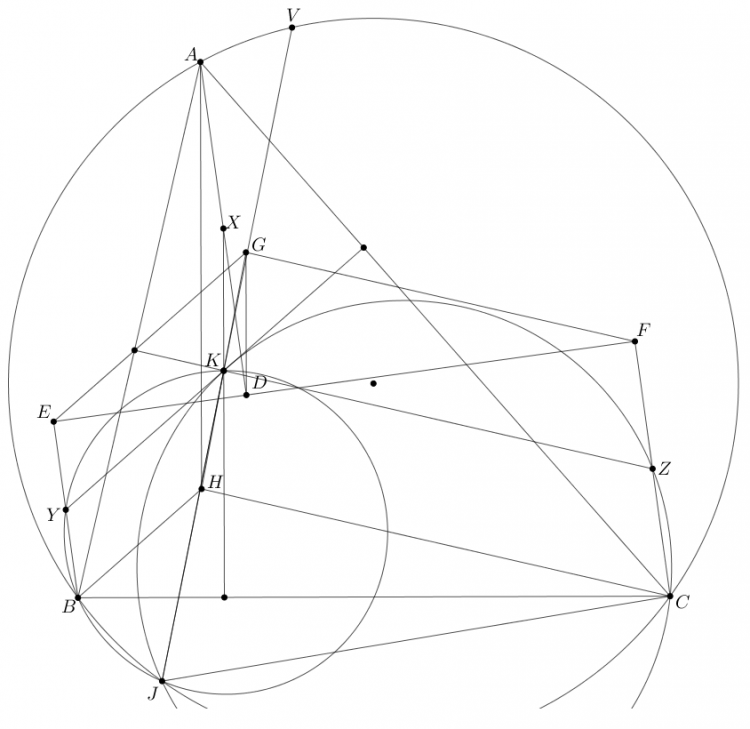
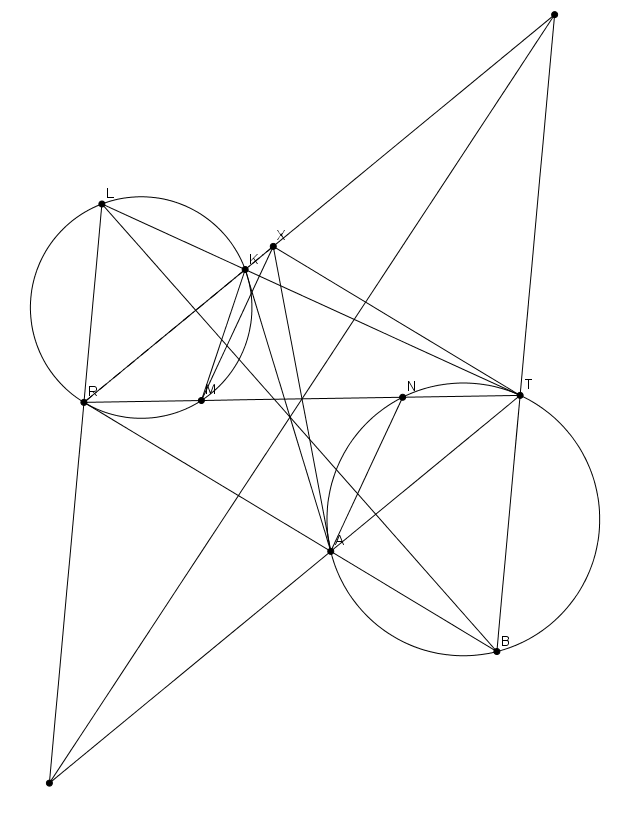
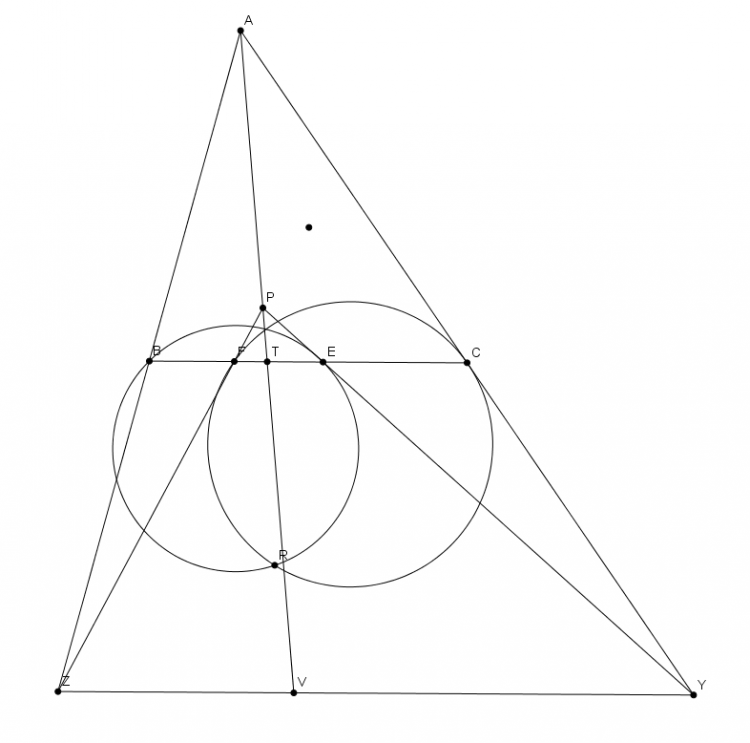
Cho tam giác $ABC$. Đương tròn $\odot(K)$ qua $B,C$ cắt $AB,AC$ tại $D,E$. Giao của $DE$ và $BC$ là $T$. Đối xứng của $B$ qua $D$ là $X$ tương tự $Y$. Chứng minh rằng $T$ thuộc trục đẳng phương của $\odot(K)$ và $\odot (AXY)$

Gọi $S$ là điểm đồng quy của $(ADE) , (ABC), AT$ , khi đó $\triangle SDB \sim \triangle SEC \implies \triangle SXB \sim \triangle SYC$ nên $X,Y,A,S$ đồng viên . Suy ra $AS$ là trục đẳng phương của $(AXY ) , (O)$ nên $T$ thuộc trục đẳng phương của $(AXY) , (K)$

Lời giải bài 1 :

Gọi $S$ là điểm của đường tròn nội tiếp với $BC$ thì $KSDL$ nội tiếp 

Ta sẽ chứng minh $P$ thuộc đường tròn $(BKS)$ và $(CLS)$ . Thật vậy , ta sẽ giả sử $P$ là giao điểm của 2 đường tròn này và sẽ chứng minh $P \in (IKL)$ , P \in IJ$

Bằng cộng góc ta có $\angle KPL = \angle IBC + \angle ICB = 180^{\circ} - \angle BIC$ nên $I \in (IKL)$ . 

Gọi $U$ là điểm chính giữa cung nhỏ của $(J)$ . Khi đó thì $\angle ULS = \angle KLS - \angle KLU = \angle KDB - \angle KAD = \angle LCS$ nên $UL$ là tiếp tuyến của $(LSC)$ . Tương tự có $UK$ là tiếp tuyến của $(KSB)$ . Mà $UL = UK$ nên $U$ nằm trên trục đẳng phương của 2 đường tròn này , suy ra $\overline{U,S,P}$

Khi đó ta có $\frac{PL}{PK} = \frac{LP}{LS}.\frac{SL}{SK} . \frac{KS}{KP} = \frac{SL}{SK} = \frac{sin \angle SKL}{sin \angle SLK }  = \frac{sin \angle LDC}{sin \angle KDB} = \frac{sin \angle LDI}{sin \angle ILD} . \frac{sin \angle IKD}{sin \angle IDK} = \frac{IL}{ID}.\frac{ID}{IK} = \frac{IL}{IK}$ nên $IKPL$ là tứ giác điều hòa 

Tiếp tục cộng góc , $\angle JKL = 90 - \angle KAL = \frac{1}{2}(\angle B + \angle C) = \angle KPL$ nên $JK,JL$ là các tiếp tuyến của $(IKPL)$ , suy ra $P,I,J$ thẳng hàng

Vậy điều cần chứng minh là đúng  Từ đây ta có $\angle BPC = \angle BPK + \angle KPL + \angle LPC = \frac{1}{2}( \angle B + \angle C) +90 $ nên tâm $(PBC)$ chính là điểm chính giữa cung lớn của đường tròn $(O)$ 

không phải đặt $x = cos a$ , mà là thay $x $ bởi $cos a$ ạ , và mình chỉ ra được phương trình đó có $3^n$ nghiệm 

tức là chỉ ra luôn $P_n(cos a) = cos _a$ có $3^n$ nghiệm , thế thì tất nhiên $P_n(x) = x$ có ít nhất $3^n$ nghiệm

$x = cos a \implies P_n(x) = cos (3^n.a) $ . Xét phương trình $cos(3^nx) = cos x $ , phương trình này có $3^n$ nghiệm $ a = \frac{k \pi}{3^n+1} , k = \overline{0 , 3^n-1}$ 

Lời giải bài 1 của em

Do $EF$ là trung trực $AI$ nên $Y$ chính là chân tiếp tuyến kẻ từ $A$ của $\triangle AZT$

$YA$ là tiếp tuyến của $(O)$ nên $Y,A$ liên hợp trong $(O)$ . $G$ là giao điểm của $HZ,L$ , $Y$ là giao điểm của $HL,ZT$ nên $G,Y$ liên hợp

Suy ra $AG$ là đường đối cực của $Y$ . Gọi $AG$ cắt $(AZT)$ tại $D_a$ thì $YD_a$ cũng là tiếp tuyến 

Từ đây có $AZD_aT$ là tứ giác điều hòa nên $AG$ là đường đối trung của $(AZT)$

Suy ra $AP$ là đường đối trung của $\triangle ABC$ nên $AP$ đi qua điểm cố định là giao 2 tiếp tuyến tại $B,C$ của $(O)$

Lời giải bài 2 của em ạ : 

1) Ta chứng minh đường thẳng qua $X,Y,Z$ vuông góc $BC,CA,AB$ đồng quy 

Gọi $H$ là trực tâm $\triangle ABC$ , $G$ là cực trực giao của $d$ đối với $\triangle ABC$ . Gọi $K$ là điểm chia $GH$ theo tỉ số $k$ . Khi đó theo định lý thales , $XK,YK,ZK$ vuông góc $BC,CA,AB$ nên đường thẳng qua $X,Y,Z$ vuông góc $BC,CA,AB$ đồng quy 

2) Ta chứng minh bài toán

Gọi $J$ là giao điểm của $(BYK) , (CZK)$ , khi đó ta có $(JB,JC) = (JB,JK) +(JK,JC) = (YB,YK) +(ZK,ZC) = (EB,BH) + (CH,CF) = (BH,CH) = (AB,AC)$ nên $J$ nằm trên $(O)$ 

Suy ra $(AXK) , (BYK) , (CZK)$ đồng quy tại $J$ nằm trên $(O)$

Gọi $V$ là giao điểm của $KJ$ với $(O)$ khác $J$ . Ta có $\angle VAC = \angle KJC = \angle KZF = \angle HCF$ cố định do $d$ cố định và $\triangle ABC$ cố định , suy ra $V$ cố định 

Lời giải bài 1 của em ạ 

Gọi $X$ là giao điểm của $(AMN)$ với $(APQ)$ . $AJ$ cắt $(AMN),(APQ)$ lần lượt tại $H,G$ . $AS$ là đường kính của $(APQ)$ . Khi đó ta có $X,H,S$ thẳng hàng và $\triangle XMN \cap H \sim \triangle XPQ \cap G$ . Ta có biến đổi tỉ số : $\frac{AJ}{AL} = \frac{AH}{AG} = \frac{AH}{AS}.\frac{AS}{AG} = \frac{XH}{XG}.\frac{PQ}{BC} = \frac{MN}{PQ}.\frac{PQ}{BC}$ . Ta có điều cần chứng minh

từ phương trình đầu suy ra $x+y \leq 3/2$ theo hàm lồi jensen 

từ phương trình 2 dùng Bun suy ra $x+y \geq 3/2$ nên $x+y = 3/2$ , đẳng thức xảy ra ở cả 2 bất đẳng thức khi và chỉ khi $x = y = 3/4$

lời giải bài 2 của em ạ

Gọi $AI$ lần lượt cắt $BC$ và tiếp tuyên tại $D$ tại $M,N$ . Ta có 2 cặp tam giác có các cạnh tương ứng song song : $\triangle END , \triangle IMC$ và $\triangle FND , \triangle IMB$ nên $\frac{NE}{NF} = \frac{NE}{IM}.\frac{IM}{NF} = \frac{ND}{MC}.\frac{MB}{ND} = \frac{MB}{MC}$ nên đường nối trung điểm $BE,CF$ đi qua $I$ theo bổ đề ERIQ

Lời giải bài 1 của em ạ 

Ta có $M$ chính là tâm bàng tiếp của $\triangle TEF$ . Gọi $G$ là giao điểm của $AM$ với $(O)$ , theo bài toán Iran TST 2017 thì $(TEF)$ tiếp xúc $(O)$ tại $G$ , suy ra $(O)$ chính là đường tròn mixtilinear ngoại của $\triangle TEF$ . Nghịch đảo cực $T$ với phương tích bất kì , ta nhận được bài toán sau 

Cho $\triangle TEF$ với $M$ là tâm đường tròn nội tiếp . $B,C$ lần lượt là tiếp điểm của $(M)$ với $TF,TE$ . $BC$ cắt $TM$ tại $O$ . $TM$ cắt $(TEF)$ tại $D$ , $(TMF)$ cắt $FD$ tại $P$ , $TP$ cắt $(TOF)$ tại $R$ . Tương tự ta có điểm $(Q)$ . Gọi $S$ là tâm ngoại tiếp $\triangle TQR$ . Khi đó $(SEF)$ tiếp xúc $M$ 

Thật vậy, gọi $G$ là tiếp điểm của $(K)$ với $BC$ , gọi $J$ là tâm bàng tiếp góc $\angle T$ của $\triangle TEF$ , gọi $U$ là trung điểm $RJ$. Ta sẽ chứng minh $U$ chính là tâm của $TQR$ , khi đó $(EUF)$ sẽ tiếp xúc $(M)$ . Thật vậy , ta gọi $X,Y$ là hình chiếu của $S,U$ lên $TP$ ; $Z,T$ là hình chiếu lên $MF$ . Ta có $TMFP$ là hình thang cân nên $XP = XT$. Ta cần chứng minh $\overline{YT} = \overline{RY}$ , điều này tương đương $\overline{YX}+\overline{XT} = \overline{RP}+\overline{PX} +\overline{XY}$ , tức là $PR = 2XY = 2ZT$ 

Thật vậy , ta có $\triangle FPR \sim \triangle FMO$ nên $PR = \frac{FP.OM}{FM} = \frac{MO.MT}{MF} = \overline{ML} = \overline{MF}+\overline{FL} = 2(\overline{ZF}+\overline{FT}) = 2\overline {ZT}$ nên ta có điều cần chứng minh là đúng 

Bài 2 : Gọi $R$ đối xứng $H$ qua trung điểm $M$ của $BC$ , $G$ đối xứng $D$ qua $H$ . Ta có $\angle MCR = \angle IBC = \angle ICB$ , $\frac{CR}{CE} = \frac{BH}{BG} = \frac{CM}{CI}$ nên $\triangle CRM \sim \triangle CEI$, từ đây suy ra $\triangle CMH \sim \triangle CIF $

Suy ra $\triangle CMI \sim \triangle CHF$ nên $\angle CHF = 90$

Lời giải bài 1 của em ạ : Gọi $X$ là giao điểm của $RK$ với đường thẳng qua $T$ song song $RA$. Khi đó $\angle RKM = \angle ART = \angle XTM$ nên tứ giác $KXTM$ nội tiếp $\implies \angle RXM = \angle XTM = \angle NAT$. Dựng hình bình hành $RX'TA$ thì $X' \in TX , \angle RX'M = \angle NAT$ nên $X' \equiv X$. Vậy ta có $RK \parallel AT \implies \angle LRA = 180 - \angle LKR = 180 - \angle LTA$ nên tứ giác $LTAR$ nội tiếp 

Suy ra giao điểm của $LR,AT$ nằm trên trục đẳng phương của $(I),(J)$. Tương tự giao điểm của $KR,BT$ nằm trên trục đẳng phương

Áp dụng định lý Pappus cho bộ 6 điểm $(LTKARB)$ ta có giao điểm của $KA,LB$ nằm trên trục đẳng phương của $(I),(J)$

tổng quát bài 2 : có thể thay điểm $O$ thành điểm $R$ bất kì. Lời giải của em ạ 

Xét phép nghịch đảo tâm $A$ biến $B,C$ thành $B',C"$, biến $Y,Z$ thành $X',Y'$ đối xứng $A$ qua $C,B$, biến $P$ thành một điểm $P"$ bất kì không nằm trên $B'C'$, biến $T$ thành giao điểm của $AP'$ với $B'C'$ , $E,F$ biến thành $E',F'$ là giao điểm của $P'Y',P'Z'$ với $B'C'$, $R$ biến thành $R'$ là điểm bất kì . $S$ biến thành $S'$ là giao của $(R'B'E')$ và $(R'C'F')$, ta cần chứng minh $R',S',T'$ thẳng hàng

Ta chứng minh bài toán mới, để thuận tiện ta lược bớt kí hiệu $'$ 

Gọi $V$ là giao điểm của $YZ$ với $AT$ . Ta có $\frac{TE}{TF} = \frac{VY}{VZ} = \frac{TC}{TB}$ nên $TE.TB = TF.TC$, suy ra $T$ nằm trên trục đẳng phương của $(BRE)$ và $(CRF)$ nên $T \in RS$. Ta có điều cần chứng minh

câu 3 : Ta cần chứng minh $Y$ là điểm Feuerbach của $\triangle ABC$ . Thật vậy , gọi $Z$ là tâm đường tròn nội tiếp $\triangle ABC$, $R$ là trực tâm $\triangle ZBC$ . Đầu tiên, ta chứng minh $A,R,P$ thẳng hàng . Gọi $V$ là giao điểm của $GZ$ với $IH$ . Áp dụng Menelaus cho tứ giác $BIHC$ thì ta có $A,V,D$ thẳng hàng . Lại có $BR \parallel AX$ do cùng vuông góc $ZC$,  và cũng có $AG \parallel DR$