manhtuan00

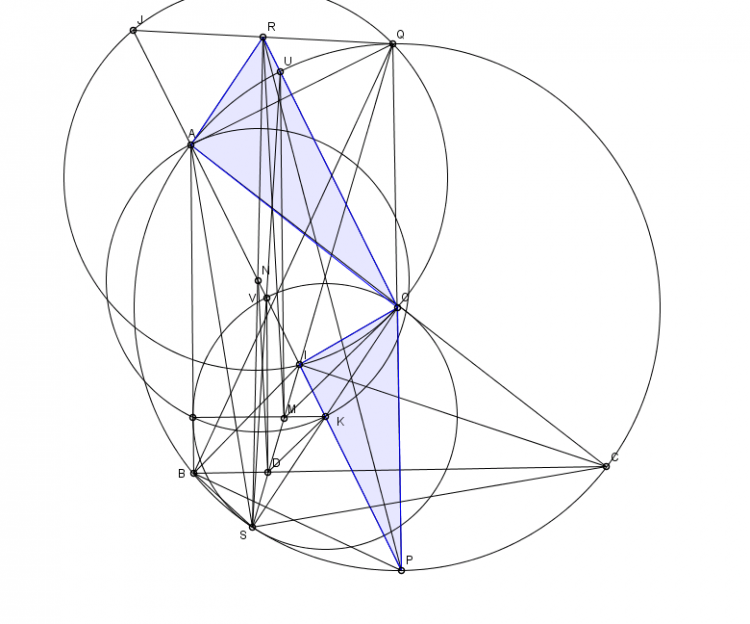
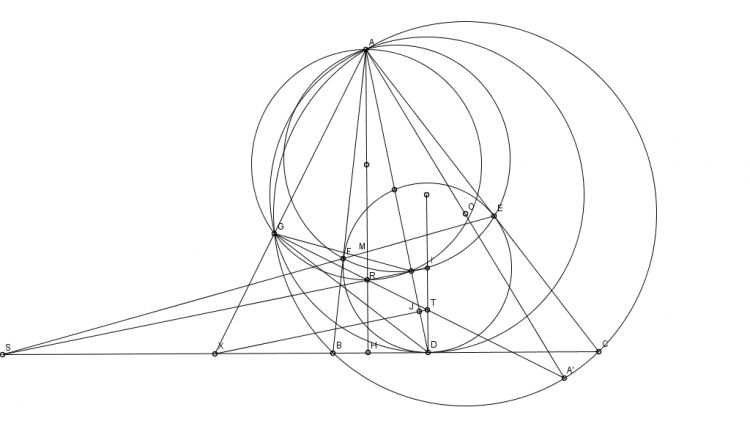
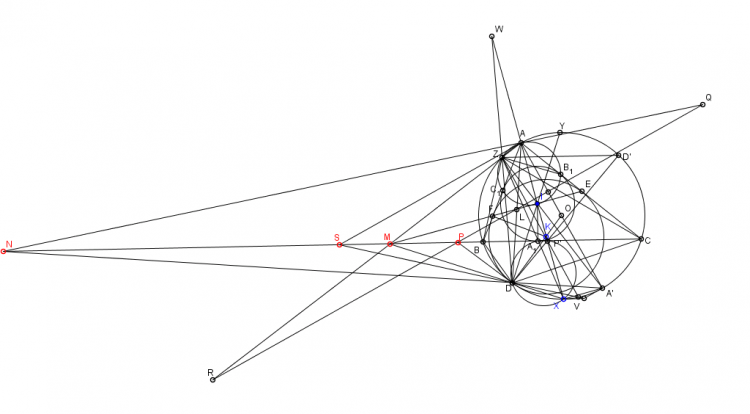
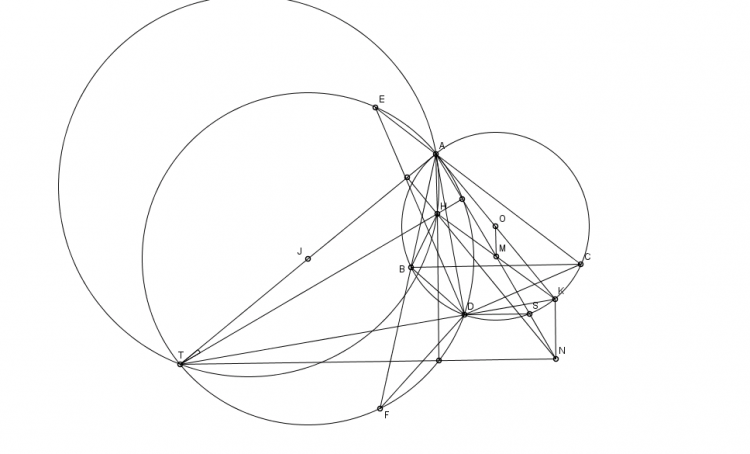
Lời giải bài 139 : ( cách của em tính khá trâu bò ạ )

Ta có $(NE,AC) = -1$ nên $\frac{\overline{NA}}{\overline{NC}} = \frac{p-a}{p-c}$

Vậy tức là $\frac{\overline{NA}}{\overline{NA}+b}= \frac{p-a}{p-c}$ nên $\overline{NC} = |\frac{b(p-c)}{a-c}|$

Lại có $AQ = \frac{p-a}{cos \angle A}$ nên $CQ = b - AQ = b - \frac{p-a}{cos \angle A}$

Áp dụng đinh lý hàm cos có : $cos \angle A = \frac{b^2+c^2-a^2}{2bc}$

Vậy ta có $\overline{CQ} = \frac{b^3+bc^2-ba^2-b^2c-bc^2+abc}{b^2+c^2-a^2} = \frac{b^3-ba^2-b^2c+abc}{b^2+c^2-a^2}$

Vậy $\frac{\overline{CQ}}{\overline{CN}} = \frac{p-a}{cos \angle A}= |\frac{(b^3-ba^2-b^2c+abc)(a-c)}{(b^2+c^2-a^2)(p-c).b}| = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Tương tự ta có $\frac{\overline{BP}}{\overline{BM}} = |2\frac{(a-b)(a-c)}{b^2+c^2-a^2}|$

Nên $\frac{\overline{CQ}}{\overline{CN}}=\frac{\overline{BP}}{\overline{BM}}$ Áp dụng bổ đề E.R.I.Q  ta có trung điểm $MN,PQ,BC$ thẳng hàng

Vì khi $p_i \neq 7$ thì sẽ tồn tại $y$ để $7y -1 \vdots p_i^{\alpha_i}$ thì $(7y-1)(7y+1) \vdots p_i^{\alpha_i}$

Chọn tiếp $x \equiv 3y$ thì sẽ có $(x-3y)(x+3y) \vdots p_i^{\alpha_i}$ kết hợp 2 điều trên thì có $x^2-58y^2+1 \vdots p_i^{\alpha_i}$

$x^2 - 58y^2+1 = x^2 - 9y^2 - (49y^2-1) = (x-3y)(x+3y) - (7y-1)(7y+1)$

Đặt $n = \prod p_i^{\alpha_i}$

Khi $p_i \neq 7$ ta chọn $7y \equiv 1$ và $x \equiv 3y (\text{p_i^{\alpha_i}}$ thì sẽ có $p_i^{\alpha_i} | x^2 - 58y^2+1$

Khi $p_i = 7$

Ta sẽ chứng minh quy nạp : với mọi $k$ thì tồn tại $x,y$ để $7^k | x^2 - 58y^2+1$

Với $k=1$ ta chọn $x = 7, y = 2$

Giả sử giả thuyết quy nạp đúng với $k$ ta chứng minh đúng với $k+1$

Ta có $x_0^2 - 58y_0^2 +1 \vdots 7^k$. Đặt $x_0^2 - 58y_0^2 +1 = 7^k. T$. Ta có $x_0, y_0$ không cùng chia hết cho 7 nên tồn tại các số $a,b$ sao cho $a . 2x_0-b.10y_0 +T \vdots 7$

Khi đó, ta chọn $X = x_0+a.7^k, Y = y_0+b.7^k$ thì $X^2-58Y^2+1 \vdots 7^{k+1}$. Ta có điều cần chứng minh là đúng

Vậy với mỗi $p_i$ tồn tại $x_i, y_i$ để $x_i^2-58y_i^2+1 \vdots p_i^{\alpha_i}$

Ta chọn $X \equiv x_i (\text{mod p_i^{\alpha_i}}), Y  \equiv y_i (\text{mod p_i^{\alpha_i}})$ thì ta có $X^2-58Y^2+1 \vdots n$. Vậy ta có điều cần chứng minh

Lời giải bài toán 121 : 

Gọi $J$ là giao điểm của $AP$ với $QR$. Do $AP \perp AQ$ nên $AP \parallel OR \implies R$ là trung điểm $OJ$.

$(K)$ tiếp xúc $(O)$ tại $S$. Gọi $U,V$ lần lượt là điểm chính giữa cung $AQ$ của $(O)$, cung $EF$ của $(K)$.

$SI$ là trung tuyến, $SA$ là đường đối trung $\triangle ESF$ nên $SA,SU$ đẳng giác trong $\angle ESF$. Từ đây ta có $S,U,V$ thẳng hàng

Thật vậy, theo bài toán 111 thì $DV \parallel UM$

Từ đây ta có $\triangle RUM$ và $\triangle NVD$ có các cặp cạnh tương ứng song song $\implies R,N,S$ thẳng hàng

Theo định lý Thales thì $\frac{OR}{KN} = \frac{OS}{KS} \implies OR = \frac{OS}{KS} . \frac{AK}{2}$

Ta có $\triangle QBP \sim \triangle AFK$ nên $\frac{QP}{PB} = \frac{AK}{KF} \implies \frac{2OS}{PB} = \frac{AK}{KS}$

Kết hợp 2 điều trên ta có $OR.PB = R^2 = OR.PI \implies \frac{OR}{OA} = \frac{OP}{PI} \implies \triangle RAO \sim \triangle OIP \implies \angle RQO = \angle RAO = \angle OIP$

$\implies RQ$ và $AP$ cắt nhau trên $(IOQ)$ tức là $JIOQ$ nội tiếp

Lại có $PR$ là trung tuyến $\triangle PQJ$ nên $PR$ là đường đối trung của $\triangle PIO$. Ta có điều cần chứng minh

P/s : bạn Bảo nhanh quá @@

$\boxed { Lời \ giải \ bài \ 109 }$ Bài toán trên tương đương với bài toán sau 

Cho $\triangle ABC$ với $I,J$ lần lượt là tâm nội tiếp và tâm bàng tiếp góc $\angle A$. $K$ là trung điểm cung lớn $BC$. $JK$ cắt $(O)$ tại $X$. $E,F$ là hình chiếu của $X$ lên $IC,IB$. Chứng minh rằng trung điểm $EF$ nằm trên trung trực $BC$

Chứng minh : Gọi $M,N, G$ lần lượt là tâm bàng tiếp góc $\angle B, \angle C$, trung điểm $BC$. Ta cần chứng minh $KG$ đi qua trung điểm $EF$, $JK$ cắt $BC$ tại $T$

Ta sẽ chứng minh $\frac{BF}{CE} = \frac{BM}{CN}$

Ta có : $\frac{BF}{CE} = \frac{BF}{BX} .\frac{BX}{CX} . \frac{CX}{CE} = \frac{cos \angle FBX}{cos \angle ECX} . \frac{sin \angle XCB}{sin \angle XBC} = \frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC}$

Gọi $U,V$ là trung điểm cung lớn $AC,AB$ khi đó 

$\frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC} = \frac{sin \angle XBJ}{sin \angle XCJ} . \frac{sin \angle XCB}{sin \angle XBC} $

Cách của Tuấn là theo hướng đáp án. Mình xin giới thiệu bài toán sau để mọi người cùng trao đổi.

 

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$, đường tròn nội tiếp $(I)$ tiếp xúc $BC$ tại $D$. $AK$ là đường kính của $(O)$. Lấy $L$ sao cho $IL\perp AD$ và $AL\perp BC$. Chứng minh rằng $KL$ chia đôi $ID$.

 

Bài toán này có 1 phần từ AoPS và 1 phần do mình tạo ra, đây là bài toán có nội dung đẹp và chính là nguồn gốc của bài toán tuần này.

Đoạn chứng minh bổ đề em làm tắt 1 đoạn ạ, em bổ sung nốt phần chứng minh $LK$ chia đôi $ID$ ạ

$(I)$ tiếp xúc $CA,AB$ tại $E,F$.$IL$ cắt $BC$ tại $M$ khi đó $M,E,F$ thẳng hàng.

Gọi $H$ là trung điểm $MD$,$AH$ cắt $(O)$ tại $G$. $S$ là trung điểm $ID$.Theo phần trên, ta có $G,S,K$ thẳng hàng

$IL$ cắt $AD$ tại $U$. Khi đó $U,D$ đối xứng nhau qua $HS$ nên tứ giác $HUSD$ nội tiếp 

Từ đây suy ra tứ giác $HGUD$ nội tiếp. Gọi $R$ là chân đường cao hạ từ $A$ của $\triangle ABC$

Có $UL \perp AD, AL \perp BC$ nên $RLUD$ nội tiếp nên ta có $\angle ALU = \angle ADR = \angle AGU$

$\implies $ tứ giác $AGLU$ nội tiếp. Từ đây suy ra $GL \perp GA \implies G,L,S,K$ thẳng hàng

$f(f(x))=f(x)+x$

Từ đề bài ta có $f$ đơn ánh, mà $f$ liên tục nên $f$ đơn điệu thực sự

Thay $x$ bởi $0$ ta có $f(f(0)) = f(0)$ nên $f(0) = 0$

Ta sẽ chứng minh $f$ là song ánh

Thật vậy, giả sử tồn tại $a$ sao cho $f(x) \neq a$ $\forall x $

Do $f$ liên tục nên $f(x) > a$ hoặc $f(x) < a$ $\forall x$

Trường hợp 1 : $f(x) > a $ $\forall x$

Nếu $f$ giảm ngặt, ta có $f(x) > a \implies f(f(x)) < f(a)$

$\implies a+x < f(x) +x < f(a)$

Từ đây ta có $x < f() - a$ với mọi $x$. Ta có điều mâu thuẫn

$\implies f$ tăng ngặt. Khi đó ta có với mọi $x$ âm thì $f(x) > f(x) +x = f(f(x)) > f(a) \implies x > a $ $\forall x < 0$ ta có điều mẫu thuẫn 

Trường hợp 2 : $f(x) < a$ $\forall x$. trường hợp này có thể chứng minh tương tự trường hợp 1

Vậy $f$ song ánh nên tồn tại hàm ngược

Gọi $g(x) = f_{-1}(x)$ là hàm ngược của $f(x)$

Đặt $f_0(x) = x, f_n(x) = f(f_{n-1}(x))$, ta có dãy như sau 

$f_{n+2}(x) - f_{n+1}(x)-f_n{x} = 0$

Ta có công thức tổng quát 

$f_n(x) = \frac{f(x)-x(\frac{1-\sqrt{5}}{2})}{\sqrt{5}}.(\frac{1+\sqrt{5}}{2})^n+(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}).(\frac{1-\sqrt{5}}{2})^n$ $(1)$

Thay $x$ bởi $g(g(x))$ vào đẳng thức ban đầu ta được dãy : $g(g(x))+g(x) - x = 0$

$\implies g_{n+2}(x)+g_{n+1}(x) - g_n{x} = 0$

Từ đây ta thu được công thức tổng quát 

$g_n(x) = \frac{g(x)+x(\frac{1+\sqrt{5}}{2})}{\sqrt{5}}.(\frac{-1+\sqrt{5}}{2})^n+(\frac{x(\frac{-1+\sqrt{5}}{2})-g(x)}{\sqrt{5}}).(\frac{-1-\sqrt{5}}{2})^n$

Thay $x$ bởi $g(x)$ vào đẳng thức ban đầu ta có $f(x) = g(x) + x$ hay $g(x) = f(x) - x$

Vậy ta có $g_n(x) = \frac{f(x)+x(\frac{\sqrt{5}-1}{2})}{\sqrt{5}}.(\frac{-1+\sqrt{5}}{2})^n+(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}).(\frac{-1-\sqrt{5}}{2})^n$

Trường hợp 1 : $f$ tăng ngặt , khi đó $f_n(x), g_n(x)$ đều tăng ngặt

Ta có $f(0) = g(0) = 0 \implies f_n(0) = g_n(0) = 0$

Với mỗi $x > 0 $ thì $g_n(x) > g_n(0) = 0$ và $f_n(x) > f_n(0) = 0$

Xét $g_n(x) = \frac{f(x)+x(\frac{\sqrt{5}-1}{2})}{\sqrt{5}}.(\frac{-1+\sqrt{5}}{2})^n+(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}).(\frac{-1-\sqrt{5}}{2})^n$

Nếu $(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}) < 0$ thì ta chọn $n$ chẵn đủ lớn 

Khi $n$ đủ lớn thì $\lim_{n\rightarrow +\infty } (\frac{-1+\sqrt{5}}{2})^n = 0$ và $\lim_{n\rightarrow +\infty } (\frac{-1-\sqrt{5}}{2})^n = + \infty$ nên $g_n(x) < 0$ ta có điều mâu thuẫn

Nếu $(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}) > 0$ ta chọn $n$ lẻ đủ lớn , ta lại có $g_n(x) < 0$ nên mâu thuẫn

$\implies (\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}) = 0$ từ đây ta thu được nghiệm hàm 

$f(x) = x . \frac{1+\sqrt{5}}{2}$

Trường hợp 2 : $f$ giảm ngặt . Khi đó $f_{2n}$ tăng, $f_{2n+1}$ giảm ngặt . Khi đó với mọi $x$ dương ta có $f_{2n}(x) > f_{2n}(0) = 0 = f_{2n+1}(0) > f_{2n+1}(x)$

Xét công thức tổng quát $f_n(x) = \frac{f(x)-x(\frac{1-\sqrt{5}}{2})}{\sqrt{5}}.(\frac{1+\sqrt{5}}{2})^n+(\frac{x(\frac{1+\sqrt{5}}{2})-f(x)}{\sqrt{5}}).(\frac{1-\sqrt{5}}{2})^n$ $(1)$

Làm tương tự Trường hợp 1 ta thu được nghiệm hàm $f(x) = x. \frac{1-\sqrt{5}}{2}$

Vậy các hàm thỏa mãn là $f(x) = x. \frac{1-\sqrt{5}}{2}$ và $f(x) = x . \frac{1+\sqrt{5}}{2}$ $\forall x $$\in $ $\mathbb R$

Giả sử $n = \prod p_i^{\alpha_i}$ trong đó $p_i$ là các số nguyên tố

Ta chứng minh tồn tại $x,y$ để $p_i^{\alpha_i}$ $|$ $(x^2-34y^2+1)$

Thật vậy ,ta có : $x^2-34y^2+1 = (x-5y)(x+5y) -(3y-1)(3y+1)$

Nếu $p_i \neq 3$,ta chỉ cần chọn $3y \equiv 1 (\text{mod} (p_i^{\alpha_i}))$ và $x \equiv 5y (\text{mod} p_i^{\alpha_i})$ Khi đó ta có $p_i^{\alpha_i}$ $|$ $(x^2-34y^2+1)$

Nếu $p_i = 3$

Ta sẽ chứng minh điều sau bằng quy nạp : Với mọi số tự nhiên $n$, tồn tại cặp số $x,y$ để $x^2-34y^2+1$ $\vdots$ $3^k$

Với $n=1$ điều trên đúng vì ta chỉ cần chọn $x =3, y = 1$

Giả sử đúng với $n = k$, ta chứng minh đúng với $n = k+1$

Giả sử $x_0^2-34y_0^2 +1 = 3^k . m$

Nếu $m$ $\vdots$ $3$ ta có điều cần chứng minh 

Nếu $(3,m) = 1$

Dễ thấy $x_0,y_0$ không cùng chia hết cho $3$ nên tồn tại các số tự nhiên $s,t$ để $m+2sx_0-68ty_0$ $\vdots$ $3$

Khi đó, ta chọn $X = x_0+3^ks, Y = y_0+3^k.t$

$\implies X^2-34Y^2+1$ $= (x_0^2-34y_0^2+1)$ $+3^k(2s.x_0-68ty_0)+3^{2k}.s^2+34.3^{2k}t^2 = 3^k(2s.x_0-68ty_0+m)+3^{2k}.s^2+34.3^{2k}t^2$ $\vdots$ $3^{k+1}$ 

Vậy điều cần chứng minh là đúng

Tức là với mọi $p_i$ nguyên tố, tồn tại $x,y$ để $p_i^{\alpha_i}$ $|$ $(x^2-34y^2+1)$

Giả sử $p_i^{\alpha_i}$ $|$ $(x_i^2-34y_i^2+1)$

Sử dụng định lý thặng dư Trung Hoa chọn $X \equiv x_i (\text{mod} p_i)$ và $Y \equiv y_i (\text{mod} p_i) \forall i$

Khi đó $X^2 - 34Y^2+1$ $\vdots$ $n$. Ta có điều cần chứng minh

Ta có $\sum \frac{a^3}{a^2+ab+b^2} = \sum \frac{b^3}{a^2+ab+b^2}$ do $\sum \frac{a^3}{a^2+ab+b^2} - \sum \frac{b^3}{b^2+ab+a^2} = \sum a-b = 0$

Vậy ta cần chứng minh $\sum \frac{a^3+b^3}{a^2+ab+b^2} \geq \frac{2(a+b+c)}{3}$

Then BĐT Bunhiakovski ta có $(a^3+b^3)$ $\geq$ $\frac{(a^2+b^2)^2}{a+b}$ $= \frac{\frac{3a^2+3b^2}{3}.\frac{2(a^2+b^2)}{2}}{a+b} \geq \frac{\frac{2(a^2+ab+b^2)}{3}.(a+b)^2}{2(a+b)} = \frac{(a^2+ab+b^2)(a+b)}{3}$

Từ đây ta có $\sum \frac{a^3+b^3}{a^2+ab+b^2} \geq \frac{a+b}{3}$. Cộng 3 bất đẳng thức với nhau ta có điều cần chứng minh

Lời giải của em ạ

Ta sẽ chứng minh bổ đề sau 

Bổ đề : $\triangle ABC$, đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$.$AI$ cắt $DE,DF$ tại $M,N$. Gọi $G$ là trung điểm $BC$. Khi đó $G$ là tâm ngoại tiếp $\triangle DMN$

Chứng minh : $M$ là giao điểm của phân giác góc $\angle A$ và $DE$ nên $BM \perp AI$

Tương tự , $CN \perp AI$

Gọi $R$ là tiếp điểm của đường tròn bàng tiếp góc $\angle A$ với $BC$, $J$ là tâm bàng tiếp

Khi đó các tứ giác $JRMB, JNRC$ nội tiếp 

$\implies \angle DRN = \angle MJC = \angle IBD = \angle DMN$ nên tứ giác $DMRN$ nội tiếp 

Hơn nữa , $\angle DNR = \angle DNI + \angle INR = \angle DCI + \angle RCJ = 90^{\circ}$ nên $DR$ là đường kính của $(MDNR)$

$\implies G$ là tâm ngoại tiếp $(DMN)$

Quay lại bài toán :

Trên trung trực đoạn $A_1A_2$ lấy điểm $A_3'$ sao cho $\triangle A_2A_3'A_1 \sim \triangle BOC$

Khi đó ta có $\angle A_3'A_2A_1 = \angle OCB $ nên $OC \perp A_3'A_2$

Tương tự ta có $OB \perp A_3'A_2$

Gọi $H$ là trực tâm $\triangle ABC$

Lại có $\triangle BHC \sim \triangle A_1AA_2 \implies \triangle A_2A_3'A_1 \cap A \sim \triangle COB \cap H$

Từ đây ta có $AA_3' \perp OH$ nên $A_3' \equiv A_3$

Nên ta có $\angle A_1A_3A_2 = \angle BOC = \angle A_2A_4A_1$ . Từ đây suy ra $A_4$ là tâm ngoại tiếp $\triangle A_1AA_2$

Tương tự ta có $B_4,C_4$ là tâm ngoại tiếp $\triangle BB_1B_2, \triangle CC_1C_2$

Có $\angle AA_4A_1 = 90^{\circ} - \angle AA_2A_1 = 90^{\circ} - \angle OAC$ nên $AA_4$ là tiếp tuyến của $(O)$ tại $A$. Tương tự ta có $BB_4,CC_4 $ cũng là tiếp tuyến của $(O)$

$AA,4,BB_4,CC_4 $ cắt nhau tạo thành $\triangle UVW$

Khi đó , $(O)$ là đường tròn nội tiếp $\triangle UVW$

Áp dụng bổ đề cho $\triangle UVW$ thì $A_4,B_4,C_4$ là trung điểm $UV,VW,WU$ 

Khi đó $(A_4B_4C_4)$ là đường tròn Euler của $\triangle UVW$ và $(O)$ là đường tròn nội tiếp nên $(A_4B_4C_4)$ tiếp xúc với $(O)$ 

lời giải của em cho mở rộng bài hình và bài 7 ạ
Bài 7 : 

Xét với $x = y = z = \frac{1}{3}$ thì ta có $c = \frac{9}{10}$

Ta chứng minh hằng số $c= \frac{9}{10}$ thỏa mãn đề bài

Ta có : $|x^3+y^3+z^3 -1| = |x^3+y^3+z^3 - (x+y+z)^3| = |3(x+y)(y+z)(z+x)|$

Và $|x^5+y^5+z^5-1| = |x^5+y^5+z^5-(x+y+z)^5| = |5(x+y)(y+z)(z+x)(x^2+y^2+z^2+xy+yz+zx)|$

Vậy ta cần chứng minh $|x^2+y^2+z^2+xy+yz+zx| \geq \frac{2}{3}$

Có $x^2+y^2+z^2+xy+yz+zx  = (x+y+z)^2-(xy+yz+zx) \geq \frac{2}{3}$ nên ta có điều cần chứng minh

Mở rộng bài 6b :