ta chứng minh bổ đề sau
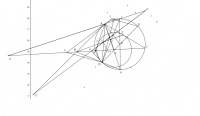
Cho tứ giác ABCD nội tiếp (O) ,K thuộc (AOC), đường tròn (K,KA) cắt AB,AD tại M,N,đường tròn (K,KC) cắt CB,CD tại S,T chứng minh MN//ST
 tuần 2 tháng 4 năm 2017.png 52.02K
58 Số lần tải
tuần 2 tháng 4 năm 2017.png 52.02K
58 Số lần tải
cho AC cắt (K,KA),(K,KC),OK tại Q,V,X.$AO\cap AO=Y$
có $\widehat{KVC}=\widehat{KCA}=\widehat{KOA}$ $\Rightarrow$ XVOYnội tiếp
ta có $\widehat{OKC}=\widehat{XCO}$ $\Rightarrow$ $\widehat{KXC}$=$\widehat{KCO}$=$\widehat{KAY}$=$\widehat{KYA}$
$\Rightarrow Y\in (K,KA)$
C/M tt QK$\cap$ OC= H $\Rightarrow$ H$\in$ (K,KC)
Ta có (AB,AC)=(AM,AQ)$\Rightarrow$ (KM,KQ)$\Rightarrow$ (OB,OC) Gọi MK$\cap$ OB=Z$\Rightarrow$ (ZK,ZO)=(HK,HO)$\Rightarrow$ HKOZnội tiếp $\Rightarrow \widehat{KZO}=\widehat{KHO}=\widehat{KCO}=\widehat{OYK}$ $\Rightarrow$ KOYHZ nội tiếp
$\Rightarrow$(KOY)$\cap$ OB=Z
Tương tự (CB,CA)=(CS,CV)$\Rightarrow$ (OB,OA)=(KS,KV). SK$\cap OB=Z'$
dễ dàng chứng minh Z'$\in$ (HKY)$\Rightarrow$ (KOY)$\cap$ OB=Z'$\Rightarrow$ Z$\equiv $Z'$\Rightarrow$ $\overline{S,M,K}$
C/m tt $\overline{K,N,T}$
 tuần 2 tháng 4 năm 2017(2).png 57.97K
59 Số lần tải
tuần 2 tháng 4 năm 2017(2).png 57.97K
59 Số lần tải
$\Rightarrow$ MN//ST $\Rightarrow PQ//ST$
$\Rightarrow$ $\overline{L,K,C}$
KC$\cap$ (K,KA)=W $\Rightarrow$ NW//TC và MW//SC
$\Rightarrow$ $\frac{JN}{NQ}$=$\frac{JW}{WC}$=$\frac{JM}{MP}$ $\Rightarrow$ $\frac{MP}{NQ}$=$\frac{JM}{JN}$

 Tìm kiếm
Tìm kiếm Nữ
Nữ













